정리노트
State Space Variables(1) 본문
지금까지..
Time Domain의 n차 Differential Equation을 Frequency Domain으로 바꿔서 해석하는 방법에대해 자세히 다루어왔다.
이번장에서는 다시 Time Domain쪽에서 시스템을 분석하는 방법에대해 다뤄보려고 한다.
(그런다고 Laplace를 안쓰겠다는게 아니라, Time Domain에서 핸들링할 수 있는 것들에대해 다뤄보려고 한다는 말이다.)
◆목차
◎ State Space Variable Model
◎ Convolution and L.T
◎ Solving State Equation
◎ Transition Matrix
State Variable Model의 아이디어는,
n차 Differential Equation을 차수는 1차로 줄이고, 줄어든 차수만큼 추가적인 변수를 늘려서
Set of 1st Order Differential Equation으로 만들어 해석하는 것이다.
이때 차수를 줄게끔 선택하는 일련의 Varible Set를 바로 State Variables라고 한다.
이런 Variables는 꼭 한가지만 있는게 아니고, 같은 시스템이어도 얼마든지 다양하게 잡을 수 있다.
State Variable Model을 이용하면, Multi Input, Multi Output을 다루는 문제를 비교적 간단하게 다룰 수 있기도 하다.

가장 간단한 예시로 Mbk 시스템을 State Variable을 통해 해석해보자.
○Simple Example - mbk
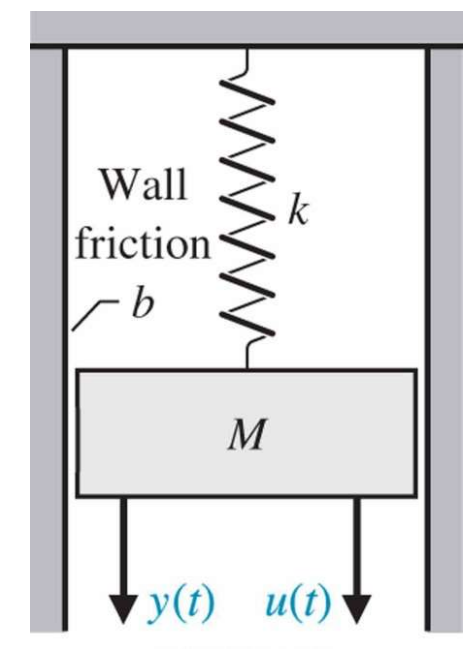

State Variable Modeling이란, n차 Differential Equation을 1차항으로 만들고, 줄어든 차수만큼 새로운 State Variable을 잡아주는 것이라고 했다.
아래와같이 State Variable을 설정해보자

이를대입하면

양쪽을 M으로 나눠주고 x2, x1에대한 1차 미분방정식으로 정리해주면

이 Set of Differential Equation은 각 State Variable이 변화에따른 시스템의 행동을 묘사한것이다.
input은 x1과 x2이고, Output은 y이며,
Output은 x1과 x2의 조합을 통해표현된다.
위의경우

State Variable을 선택하는 특별한 기준이 있는것은 아니며,
주어진 시스템에서 얼마든지 다르게 잡을 수 있다. 단, 원칙상 State Variable을 가능한 작게잡아
Redundant State Variable이 생기지 않도록 해야한다.
State Variables의 개수는 시스템을 표현하는 Differential Equation의 차수와 같으며,
Transfer Function의 분모의 차수와도 같다. (after cancelling common factors in the numerator & the denominator)
RLC회로도 간단하게 살펴보자
○Simple Example - RLC

여기서 KCL, KVL을 적용하여 mck와 Equivalent하게 State Variable을 잡아도 되지만,
이번엔 조금 다르게 에너지 측면에서 시스템을 해석해보자.


*여기서 State Variable은 물리량이 서로 달라도 상관없음을 알 수 있다.
나중에 Transforming할때도 다루겠지만 한 변수안에 여러가지 물리량이 섞여있을 수도 있다.
즉, 시스템을 표현할 뿐 State Variable은 특정 물리량과는 전혀 관계가 없다.
전류 법칙과, 전압법칙을 적용하면 다음과 같다

여기서 state Variable을 각각

로 잡았으므로, 다시정리해보면

그리고 Output은

○ State Differential Equation을 조금더 General하게 표현해보도록 하자.
선택한 State Variable Set를 다음과같이 표현해봤을때


이 된다.
여기서, A는 System Matrix, B는 input Matrix가 되며,
Output Equation인

에서 C는 Output matrix, D는 FeedForward Matrix가 된다.
Mass-Spring-Damping으로 이걸 적용해보면

System matrix, Input matrix, Output matrix, FeedForward matrix가 뭔지 한눈에 알 수 있다.
x'을 표현하는 x와 u의 조합에 따라 System matrix, input matrix를 알수 있고,
x를 표현하는 x와 y의 조합에 따라 output matrixm feedforward matrix를 알 수 있다.
○ Example - Two Rolling Cart

여기서는 input이 두개지만,
state Variable로 하나씩 더잡아서 4개의
State Variable set로 시스템을 해석할 수 있다.
먼저,
시스템의 Governing Equation은

State Variable를 다음과같이 설정해보자


즉, State Variable Set는

이에대해서 General Form으로 전체 시스템을 나타내면


◎ Convolution and L.T
Laplace Transform에서 중요하게 다루어지는 성질 중 하나가,
그것이 곱에대해서는 닫혀있지 않다는 것이다.
t도메인에서 곱이, S도메인에서 곱을 의미하지 않는다.
수식으로 증명해보면 다음과 같다.

proof

Convolution에 대한 자세한 증명은 일단 생략하고 결론만 보자.
(이에 이론적인 부분에대한 것은 유튜브에 아주 잘 나와있다)
Convolution에대한 정의는 다음과 같다.

그리고 이는 다음을 만족한다.

즉, Laplace변환시킨 S도메인에서 두함수의 곱은 두함수의 Convolution된 함수를 Laplace한것과 같다.
이를 다시말하면,
S-Domain에서 두 함수의 곱의 inverse Laplace Transform은,
두함수의 Convolution과 같다는 말이된다.
Convolution은 State Equation을 푸는데 중요하게 쓰이는 성질이다.
아래 Solving State Equation 파트에서 응용해보면서 조금더 자세히 보도록 하자.
◎ Solving State Equation
우선 위에서 다룬 Convolution을 어떻게 사용하는지 보자

이런 식이 있다고 했을때, 이를 Laplace Transform 하고, input, output에대해 정리해주면

여기서 다시 I.L.T를 진행해주는데 두번째 텀이 S도메인에서 두개의 함수의 곱으로 표현되어있다.
이럴경우 t도메인에서 Convolution 형태로 inverse해주어야 한다.

**Laplace변환을 굳이 이용하지 않더라도, 풀이가 가능하다.
이 결과로 Convolution의 결과가 맞다는 정도만 확인해두자.

여기까지가 준비운동이었고,
이제부터 본격적으로 General한 State Equation을 풀어보도록 하자

앞서봤던 예제에서 a,b라는 스칼라를 각각 System Matrix A와 Input Matrix B로 바꾸어 주었다.

뒤에 Convolution만 없으면 공업수학내내 봤던 x' =Ax의 해와 같다.
결국 input Term이 추가되면서 Convolution형태로 식이 정리된 것이다.
이건 결론이고
지금부터 이에대한 증명을 다양한각도에서 뜯어보도록 하겠다. 사실 결론만 알고있어도 상관없을것 같지만
○ input이 없는 State Equation

먼저 input이 없다고 놓고 시작해보자



여기서 각 Term을 하나하나 비교해보면

일반항 bk에대한 규칙을 찾았다. 이를 다 대입하면


여기서 테일러 급수를 적용하면

여기서 한가지 체크해야할 것은, A가 Scalar가 아니라 Matrix라는 점이다.
Matrix Exponential은 일반적인 Exponential과 비슷한 성질을 갖는다.



e^(At)의 inverse는 e^(-At)임을 알 수 있는 부분이다.
여기서 체크해 두어야 하는건
스칼라가 아니라, 행렬의 연산은 늘 조심히 다뤄야한다는 것이다.

또 한가지 착각하면 안되는 내용은 다음과 같다.

여기까지가 t domain에서 완전 쌩으로 Solution을 구한거고,
Laplace Transform을 이용하면, 등비수열의 곱처럼 생각되어 비교적 쉽게 구할 수 있다.





비교적 쉽게 결론이 도출된다.
○ input이 있는 State Equation
t 도메인에서 먼저 해결해보자.

깔끔하게 결론이 나온다.
라플라스 변환을 통해 조금더 간단하게 해결해보면

Matrix 형태로 쓴다는 것 빼면, 앞서 Convolution과 함께 정리한 내용과 같다.

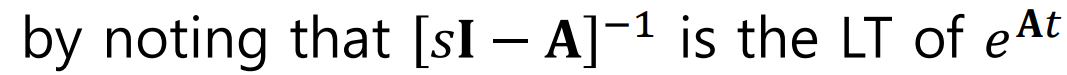
◎ Transition Matrix
위의 식에서 e^(At)를 state Transition Matrix 또는 Fundamental Matrix라고 표현하며,
이를 통해 X(t)를 조금더 General한 형태로 표현하면 다음과 같다.


state Transition Matrix는 시스템의 'unforced Response'.. 즉, 외부 input이 없을때 반응을 나타낸다.
이 Matrix를 이용해서 input= 0일때의 시스템을 일반화하여 표현하면 다음과 같다.

여기서 State Transition Matrix의 각 component는 다음과 같이 생각할 수 있다.

그리고, 다음과 같은 성질을 만족한다

이상 여기까지 State Variable로 Model을 어떻게 해석하는지 다뤄보았고,
다음 포스팅 (2)에서 Signal Flow와 Block Diagram 을 활용해
전체 시스템에 대한 State Varible 모델 해석법을 다뤄보도록 하겠다.
'Control > 자동제어' 카테고리의 다른 글
| The Performance of Feedback Control Systems (1) (0) | 2021.11.12 |
|---|---|
| State Space Variables(2) (0) | 2021.10.17 |
| Mathematical Models of System(2) (0) | 2021.10.16 |
| Mathematical Models of System(1) (0) | 2021.10.15 |
| Laplace Transform 정리(2) (0) | 2021.10.12 |




