정리노트
State Space Variables(2) 본문
(1)에서, State Space Variable들을 가지고 시스템을 어떻게 해석하는지, 그것이 어떻게 유용하게 쓰이는지 자세히 다뤄보았다.
이번 포스팅에서는 시야를 넓혀서, signal Flow, Block Diagram애서의 State Variable적용에관해 다뤄보려고 한다.
◆목차
◎ Canonical Form (Signal Flow & Block Diagram)
◎ Alternative Signal Flow & Block Diagram
◎ Transforming the state Equation
◎ Diagonalizing a system Matrix
◎ finding Transfer Function from State Equation
◎ Canonical Form (Signal Flow & Block Diagram)
앞서, State Variable을 정하는 방식은 하나가 아니며, 사용자의 마음에 따라 다양하게 잡을 수 있다고 히였다.
즉, Signal Flow와 Block Diagram도 그에 따라서 하나가 아니게 되는 것이다.
여러개를 잡을 수 있지만,
그중 자주 쓰고 대표적인 정형화된 형태, 즉 Canonical Form이 있는데,
앞서 봤던 Mason's signalFlow Rule도 결국 Canonical Form중 한가지 형태인 것이다.
아래 식을 통해 자세히 알아보자.


분모의 차수가 분자보다 크거나 같은 Transfer function이 위와같이 주어졌을때,
분모 분자에 s^(-n)을 곱하면

앞서 Mason rule과 비교하며 자세히 살펴보자.
Mason Rule의 결과는 다음과 같았다.


그리고 다시,우리가 구한식과 비교해보면

이제 뭔가 보이기 시작한다.
Mason 규칙에 따라서, 위의 두가지 TF식 비교를 통해
다음아래내용들을 파악할 수 있다.
- Transfer Function의 분모는 "1 - Non Touching Loop Gain"이다.
- n차 시스템이라면 ... n개의 State Variables가 필요하다 (모르겠다면 초록색 하이라이트 부분을보라)
- Signal Flow에서 위 식의 초록색부분은 Forward Path Factor 와 같다. (자센한건 아래내용에 나온다)
- minimum set of State Variables를 선택하는게 원칙이라고 했다.
이말인 즉, 시스템의 차수를 최소한으로 가져가야 한다는 말과 같고
결국 이말은 또, mimnimum number of integrators 과 같은말이 된다.

... 1/s가 적분기인것은 Laplace Transform에서 다뤘던 내용이다
위에서 설명한 내용들을 이제 Signal FLow, Block Diagram으로 가져가보자.
먼저 분자는 0차, 분모는 4차 System을 예시로 들어보자


이를 Signal Flow로 표현해 보면?
Mason's Rule을 잘 생각하여 따라가다보면 아래와 같이 그릴 수 있다.
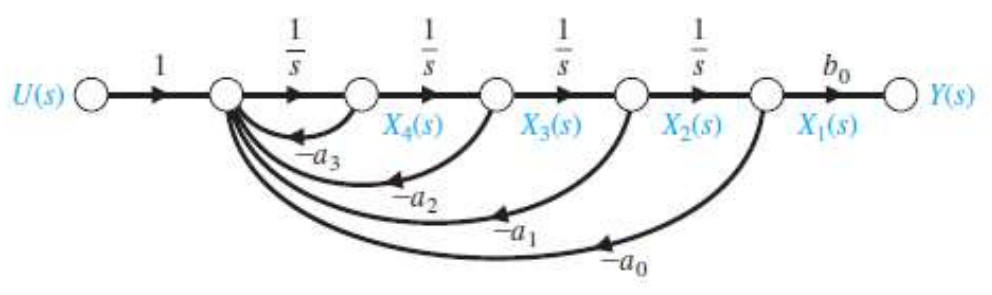
이를 조금 더 자세히 살펴보기 위해,
State Variable을 설정해보자.

이를 t domain 미분방정식으로 표현하면

(초기값은 모두 0이라고 가정)
즉.
State Variable set를 아래와 같이 설정할 수 있다.

x4'을 구해보면,

즉,
x4' + a3x3' + a2x2' + a1x1' + a0x1 = x4' + a3x4 + a2x3 + a1x2 + a0x1 = u
....(내가봐도 헷갈리는데 잘따라가보면 쉽게 이해할 수 있다)
즉, x', x, u 쌍으로 식전체를 정리해보면(State Variable Model로 정리해보면)

그리고 Output은

이를 Block Diagram으로 표현하면

앞서 그렸던 Signal Flow Graph모습과 똑같은 모습인걸 알 수 있다

여기서 이야기를 조금 더 확장해서, 보다 일반적인 경우를 살펴보자
분자의 차수가 0차 Constant가 아니라면 어떻게 될까?
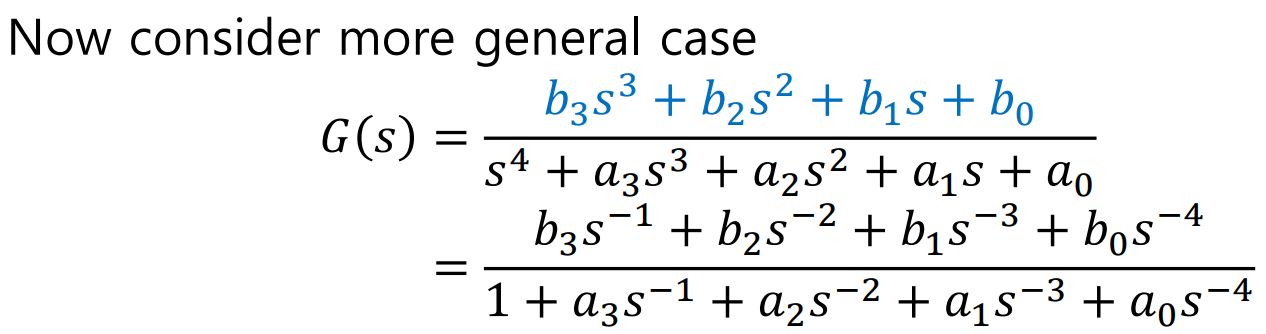
Mason's rule에 따라, Transfer Function 분자의 의미는
Forward Path Gain값과, Touching Loop Gain을 제외한 Cofactor Gain값을 곱한 값이다. (말로 설명하기 참 어렵ㄷ)
즉, 분자에 4개의 차수가 존재한다는 것은, 4개의 Path가 있는 것이라 추측해볼 수 있다.
이를 실제 구현해보면 다음과 같다.
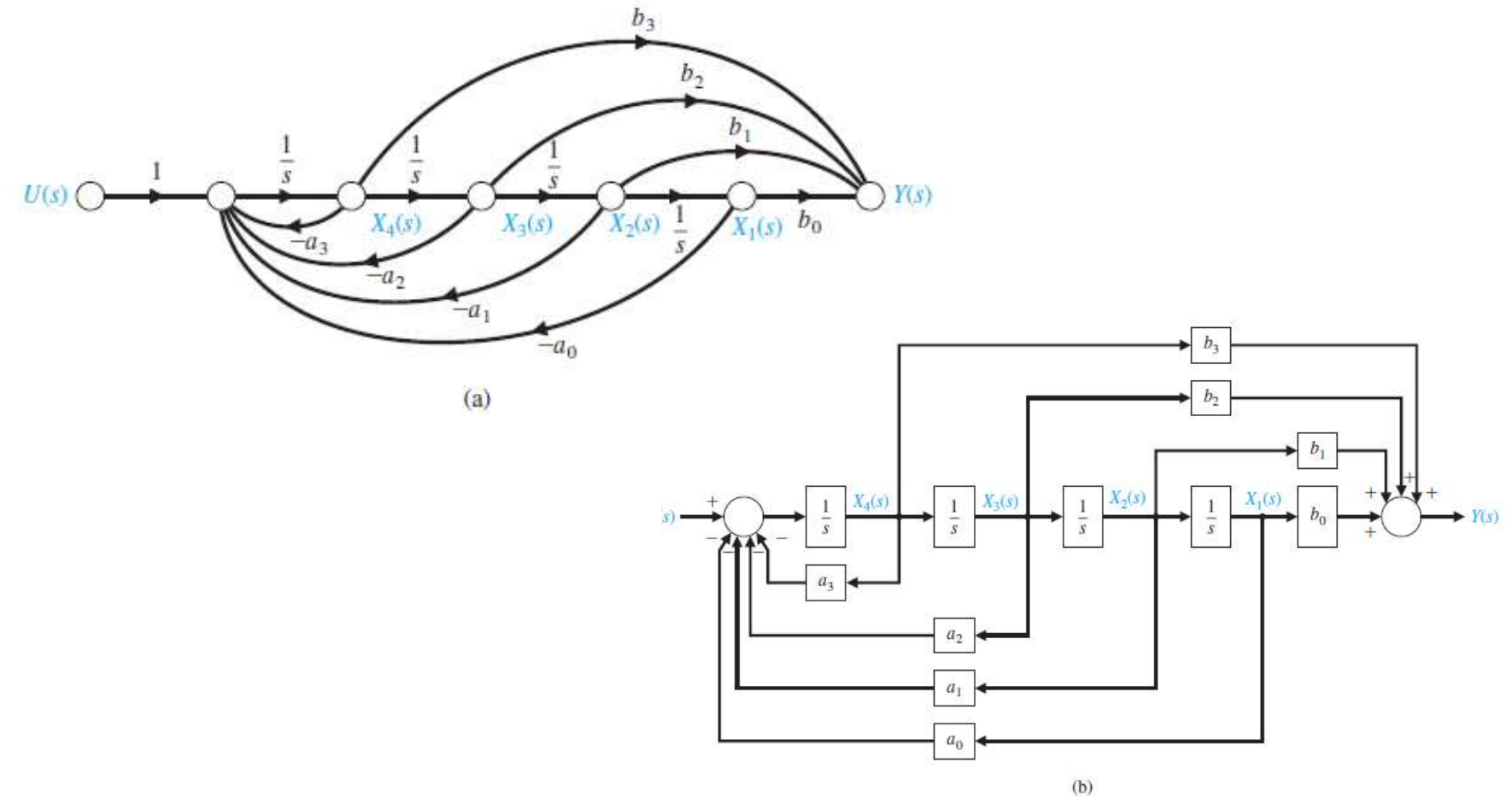
이런 모양을 띄는 Signal Flow와 Block Diagram을
Phase Variable Canonical Form이라고 하는데, 이를 좀더 자세히 정리해보자.
○ Phase Variable Canonical Form
signal Flow의 node는 signal이며,
Phase Variable Canonical Form에서 각 node끼리 연결된 TF는 integrator이다.

즉, 위의 식을 달리말하면
x3는 x4의 integral,
x2는 x3의 integral,
최종 x1은 x2의 integral이된다.

이를 조금 General 하게 Matrix형태로 Phase Variable Canonical Form을 설명하면

지금까지 본건 Canonical Form중에 Phase Variable Canonical Form을 살펴봤다.
Phase Variable Canonical Form의 분자 coefficient인 b0~b3의 위치를 기억해두자.
○ Input Feedforward Canonical Form
아래 서로 비슷해 보이는 두개의 Signal Flow를 살펴보자.

오른쪽 signal Flow Graph는
Phase Variable Canonical Form의 signal Flow Graph이다.
두 signal flow에서 모든 forward path와 feed back loop, 그리고 모든 Loop들 끼리도 서로 touch하므로,
Mason's Rule에 의해서 두 signal Flow의 Transfer Function은 서로 같음을 알 수 있다.
그렇다면
State Variable set는 어떨까?

앞서 Phase Variable Canonical form에서 b형태를 비교해보면,
feed forward가 U(s) input에서 시작되어 각각 node에 전달된다는 걸 볼 수 있다.
위 Signal Flow graph형태가 input Feedforward Canonical Form 이라고 불리는 이유다.
이를 수식으로 표현하면

***순간적으로 헷갈릴 수 있는 부분****
한 Transfer Function, 즉 시스템을 표현하는데 State Variable set이 여러개일 수는 있지만,
Signal Flow와 Block diagram을 표현하는 State Varaible은 한가지로 유일하다.
즉, 위의
input Feedforward Canonical Form식에서 x1',x2',x3'에관해 정리한것과
Phase Variable Canonical Form식에서 x1',x2',x3'에관해 정리한것은 서로 다르다는점 헷갈리지 않아야한다.
*****
이를 Matrix로 정리하면

○ Input Feedforward Canonical Form / Phase Variable Canonical Form
Note: 자, 앞서
Input Feedforward Canonical Form 의 State Variable Set과
Phase Variable Canonical Form 의 State Varible Set이 서로 다르다는 언급을 했었다.
지금까지 해본 것은
같은 시스템, 즉 같은 Transfer Function을 표현하는 방법에서
다른 State Variable Set을 선택하여 Canonical하게 표현한 것이다.
그렇다면
서로 다른 State Variable끼리는 어떤관계를 가지고 있을까?
놀랍게도 서로 Linear한 관계이다

이말인 즉,
한 State Variable를 정할 수 있으면, 그것을 Linear Transform한 무한한 State VariableSet를 선택할 수 있는것이다.
아래 식을 통해 간단히 생각해보자

위의 Transfer Function은.. 보통 n차 Differential Equation에 대한 Single Output을 표현한다.
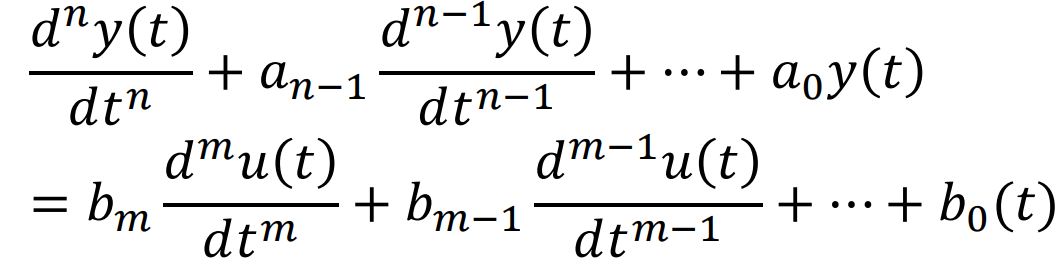
->위의 식에서 Phase Variable Model 또는 Input Feedforward Model을 사용해서
n개의 1차 미분방정식을 정할 수 있다는 말과 같다. (그리고 두 State Variable Set는 서로 Linear한관계다)
이에 대해서는 ◎ Transforming the state Equation 에서 조금더 자세히 다뤄보도록 하겠다
◎ Alternative Signal Flow & Block Diagram
지금까지 살펴본 두가지 State Variable외에 다른 State Varible Set를 살펴보자.
○ Physical State Variable model
.. 딱히 어떤 Form을 따르는 것은 아니고
그냥 물리적인 의미를 가진 물리량 그 자체를 State Variable로 선택한다는 말이다.
아래 DC motor Controller 예시로 알아보자.
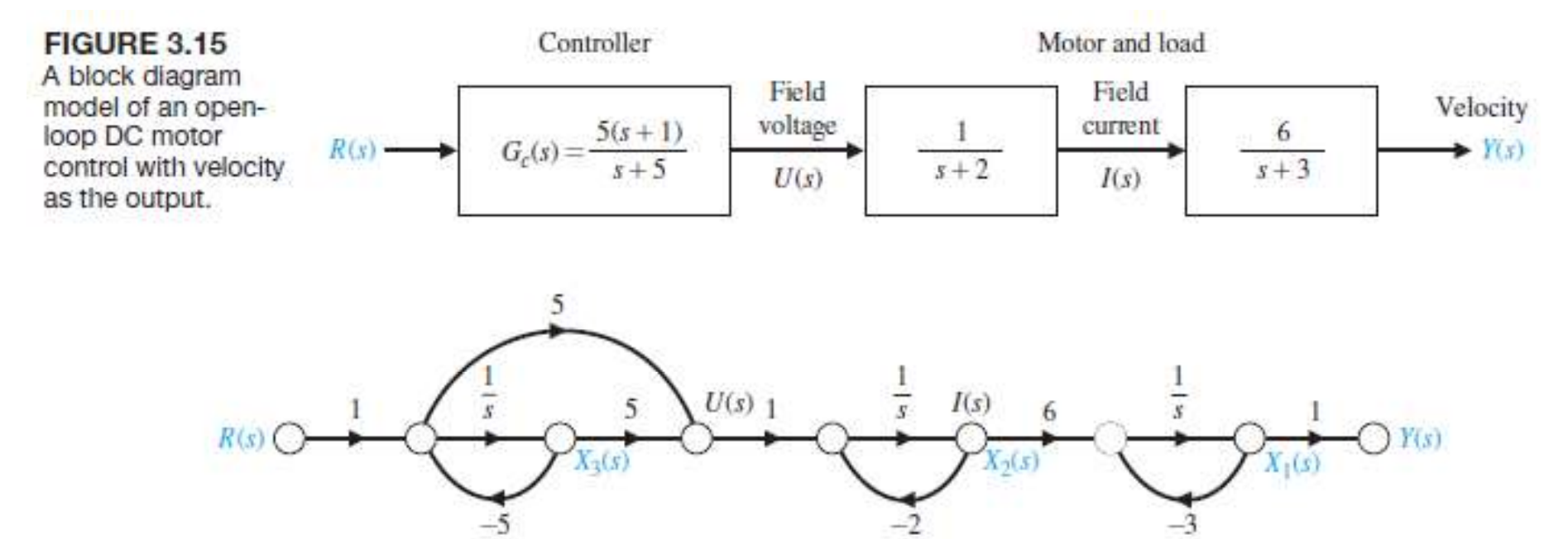

특별한 내용은 아니니, 응 그렇구나 하고 넘어가면 된다
○ Decoupled State Variable Model
이것도 응 그렇구나 하면되는데,
여기서 조금 체크해둘 내용은 State Variable이 'Decoupled'되어있다는 것은,
곧, Matrix가 'Diagonal'하다는 것이다


이제 Decoupled라는 단어의 의미를 알 수 있을 것이다.
이런 Decoupled State Variable Model은 Diagonal Canonical Form이라고도 불린다.
여기서부터 선형대수적인 개념이 조금 들어간다.
위의 예시처럼,
만약 System Matrix가 Diagonal한 형태라면, 그것의 Diagonal Terms는 System의 Pole과 같다는 것을 바로 알 수 있다.
Transfer Function에 대한 State Variable은 하나가 아니라 무수히 다양하게 잡을 수 있으며,
각 State Variable Set끼리 Linear 한 관계라고 앞서 언급했었다.
즉, System에 Pole이 존재한다면(Characteristic Equation에 해가 존재한다면,)
State Variable Set를 Diagonal Canonical Form형태가 되도록 잡을 수 있다는 말과 같다.
-> Diagonalize!
만약 Pole이 없어서 Diagonalization이 안되는 행렬의경우,
선형대수 Jordan Form 컨셉을 사용해서 Diagonalization 비슷하게 해줄 수 있는데
이는 Jordan Canonical Form이라고 불린다.
이 부분에대한 내용은 선형대수적인 내용이라,
일단 여기서는 자세히 다루진 않겠다.
이렇게 Diagonalize해주는 내용은 선형대수에서 많이 다루는 개념인데,
어떤 시스템의 행렬식을 잘 핸들링 할 수 있게되기 때문에 중요하게 다루어지곤 한다.
밑에 따로 ◎ Diagonalizing a system Matrix 파트에서 이를 다뤄보도록 하겠다
◎ Transforming the state Equation
n개의 State Variables set에 대해서 이를 Linear Transformation하여
다른 State Variable Set를 가질 수 있음을 위에서 확인했다.

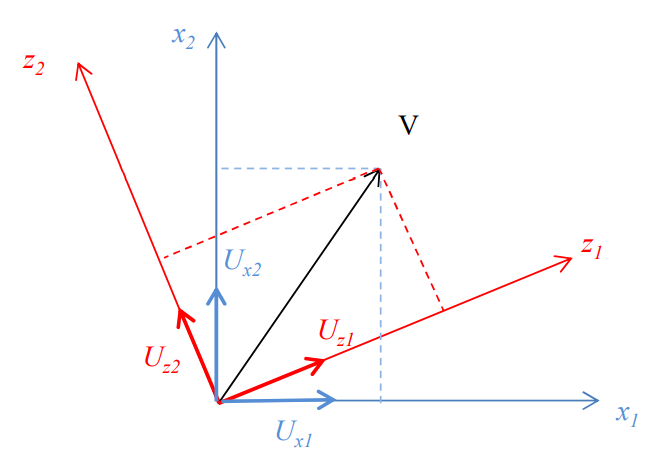

위의 내용들은,
선형대수건, 공업수학이건 주구장창 다루는 내용이니까 일단 가볍게만 정리하고 넘어가겠다.
여기서 포인트는,
Transformation후에도 Tranfer Function이 보존되는가? 에대한 증명이다
증명은 다음과같다.

Laplace 변환

식을 정리해보면

이를통해 어렵지않게 Transfer Function을 구할 수 있다

자, Transition Matrix Form을 이용해서 위와같이 TF를 정의했고,
이제 Matrix를 변환하면 어떻게 되는지 살펴보자.
여기서부터는 거의 선형대수내용이다.



즉, 이를 위의

이 형식을 이용해서 Transfer Function을 구해보면

여기서
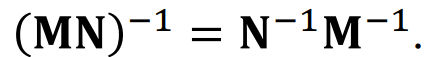
임을 기억하고 심호흡 한번하고 정리해보면

결과, Transfer function은 보존됐다는 걸 알 수 있다.
사실 결과만 알아도 크게 상관없는 부분이다.
이 내용에서, P가 만약 System Matrix의 Eigen vector라면,
P^(-1)AP의 결과가 A의 Diagonalization한 결과가 되는데, 여기에 대한 자세한 내용은 선형대수적인 내용이니
일단은 생략하고,
P가 A의 Eigenvector라는점,
그리고 State Variable Set를 Diagonalization을 통해 Handling하기 편하도록(Decoupled Form) 만들 수 있다는점을 기억해두면 된다.
'Control > 자동제어' 카테고리의 다른 글
| The Performance of Feedback Control Systems (2) (0) | 2021.11.13 |
|---|---|
| The Performance of Feedback Control Systems (1) (0) | 2021.11.12 |
| State Space Variables(1) (0) | 2021.10.16 |
| Mathematical Models of System(2) (0) | 2021.10.16 |
| Mathematical Models of System(1) (0) | 2021.10.15 |




