정리노트
The Performance of Feedback Control Systems (1) 본문
우리가 시스템을 열심히 해석하는 이유는
결국 시스템을 'Desired', 원하는 방식으로 구동하기 위해서이며,
우리는 상황에 맞게 적절한, 'Desired Performance'를 내기위한 컨트롤러를 제작해야 한다.
이 컨트롤러가 적절히 구동하는지 평가하기 위해선 크게 두가지로 나뉘며, 이는 다음과 같다.
- 'Transient Response' : 시간이 지남에 따라 사라지는 Response
- 'Steady-State Response' : 시간이 지나도 남아있는 Response
(4장이 FeedBack System인데 생략)
이번장에서는 시스템중에,
FeedBack System의 Performance를 어떻게 평가하는지 살펴보려고 한다.
목차는 다음과 같다.
◆목차
◎ Test input Signals
◎ Poles & Zeros
◎ 1st Order System
◎ 2nd Order System
◎ Performance Measure
◎ Evaluation of Tp, Tr, P.O. , Ts
◎ Pole Locations & Tp, P.O. , Ts
◎ Response & Pole Locations
◎ Test input Signals
이부분은 크게 중요치않으니 응 그렇구나 정도로 넘겨들으면 될 부분이다
우리가 원하는것은, Specific Input에 따라 시스템이 특정한 방식으로 동작하는 것이다.
input으로 알려진 Signal 표현식은 이미 많은데,
보통 Response를 보기위해 집어넣는 표준화된 input 신호는 아래 표와 같다.

그리고 각 Input들은 아래와 같은 관계를 갖는다.

그리고 unit Impulse Function에대한 식은 아래와 같다.



그리고 이런 Unit Function은 아래와 같은 Sampling Property를 가진다.

이런 관계를 Convolution과 연결지어 생각해보면

◎ Poles & Zeros
Laplace Transform이후, S도메인상에서 Output혹은 TF의 Signal을 분석할때,
분자의 근과 분모의 근으로 해석을 진행한다. 이때 분자의 근을 Zero, 분모의 근을 Pole이라고 한다.
(Bode Plot 상에서 Pole은 아래 방향으로 꺾이는 지점을 말하며, Zero는 윗 방향으로 꺽이는 지점을 말한다)

◎ 1st Order System
System의 차수는, Characteristic Equation의 차수를 말한다.
Characteristic Equation, 특성방정식을통해 시스템이 어떻게 거동되는지 알 수 있는데,
우선 1차 시스템이 어떤것인지 먼저 예시를통해 살펴보자

이에대한 Output식을 정리해보면

이를 Time Domain으로 Inverse Laplace 역변환을 통해 표현해주면
여기서,
시간이 점점 흐를때(t가 점점 커질때,) 첫번째 Term인 2/5는 계속 남아있는 반면, 두번째 Term 3/5*e^(-5t)는
점점작아지며 결국 0으로 수렴한다.

위의 예시에서 이런 Response에대해 용어정리를 간단히 해보면 다음과 같다.
Output Signal에 2/5라는 Term이 존재하는 것은,
시스템에 가해진 어떤 input의 힘에 의해서 시스템의 거동이 특정한 방향쪽으로 이동하고 있음을 의미하며,
이런 반응을 Forced Response라고 한다.
두번째 Term인 3/5*e^(-5t)이 존재하는 것은,
외부 input에 의해 발생되는 것이 아닌, 그 시스템자체의 특성으로 인해 input이 들어왔을때 어떻게 반응하는가? 를 의미하며, 이런 반응을 Natural Response라고 한다.
이런 1차 시스템을 General하게 표현하면 다음과 같다.

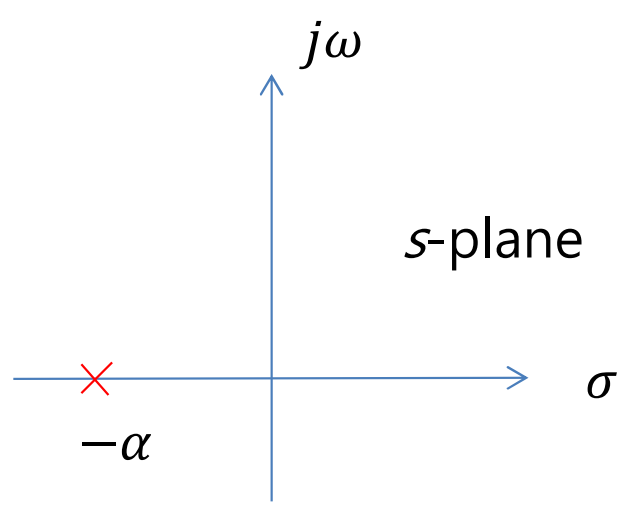
만일 input이 Step input이라면,

이 Output을 Forced, Natural Response로 나눠보면


뒤에서 Tp, Tr, Ts, P.O 에 대해서 다룰때 자세히 언급하겠지만
이 시스템의 특성을 나타내는 파라미터 중,
시상수(Time Constant), Rise Time , Settling Time은 다음과 같다.

그리고 이에대한 Bode Plot은

◎ 2nd Order System

Step input이 가해진 2차 System이 위의 그림과 같이 있다고 가정해보자.
이때, System Pole 두쌍과, 원점에 놓인 Input Pole, 총 3개의 Pole이 존재하며,
Under Damped, Over Damped, Undamped, Critical Damped 상황에 대한 각가의 해석은
각각 다음의 예시로 설명할 수 있다.
○ Overdamped Response



○ Underdamped Response



○ Undamped Response



○ Critical Response

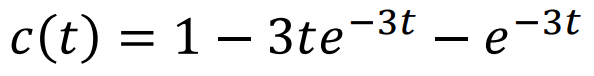

여기까지 간단하게 Summary해보면

이런 예시들에대한 General한 표현은 다음과같다.




이런 2nd Order System에 Step Response를 input으로 넣은 예시로
Transfer Function이 2nd Order System인 경우를 살펴보자. (과정은 복잡하니 결론으로 바로 넘기는 것 추천)
○ Step input Response



여기서, Step Input이 주어지므로,

이를 Pole과 Zero로 나누기위해 아래와같은 과정을 거쳐보자.

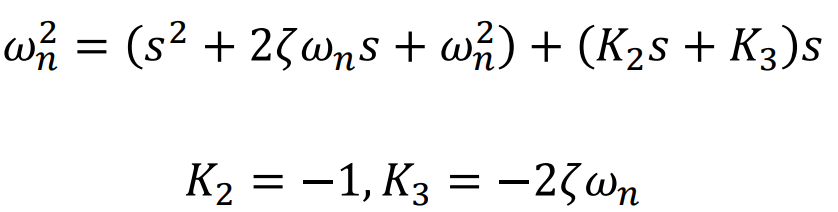
심호흡 한번하고
이를 한번더 정리해보면

여기서 3개의 Term으로 아래와 같이 정리해보면


..... 복잡했지만 결론은 아래의 식 하나로 정리된다


이로써 Step Input에 대한 2차 Feed Back System의 Output Signal 식을 정리하였다.
여기서 Damping Ratio값에 따라 시스템의 움직임을 살펴보면
아래그림과 같다.

최종 Summary는 아래와 같다.

○ Impulse input Response



◎ Performance Measure
지금까지 각 input에 따라 시스템이 어떻게 거동하는지 살펴보았다.
이제부터 시스템에대해서 이러한 거동들을 어떻게 평가해야하는지 알아보도록 하자.

크게 4가지를 살펴볼 수 있다
1, Percent Overshoot(P.O) = (Overshoot - Final Value) / Final value
2, Setttling Time = Steady State Value 영역과 특정 %만큼(보통 2%) 가까워졌을때의 시간.( = 4*Time Constant )
3, Rise Time = Step input이 주어졌을 때 10%에서 90%까지 (대략) 걸리는 시간.
4, Peak Time = Peak Value (Overshoot)을 찍었을때의 시간
다음 섹션은 Signal Performance Measure의 이런 4가지 index에대한 내용이다.
자세히 알아보자.
◎ Evaluation of Tp, Tr, P.O. , Ts
- Peak Time (Tp)
Magnitude가 Peak지점(Overshoot Point)에 도달했을때의 시간을 말한다.
보통 미분을 통해서 기울기가 0이되는 첫번째 지점의 시간으로 Time을 설정한다.
위의 Step input이 들어간 2차 시스템의 Output식을 통해서 예를 들어보면 다음과 같다.

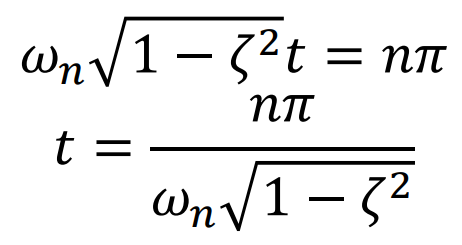

- Rise Time (Tr)
10% -> 90%(대략) 지점까지 Signal Magnitude가 도달하는데에 걸리는 시간을 의미하며, 이는 다음과같이 표현할 수 있다.

- Percent Overshoot(P.O.)
Percent Overshoot의 정의는 다음과 같다.

* 일반적으로 Fv(Final Value)는 input의 Magnitude를 말하지만 많은 시스템은 Desired Input의 Magnitude와 다른값을 가진다.
* 다만 포스팅에서 다룰 input 의 Maginitude, Final value는 1로 설정하고 접근한다.
- Settling Time (Ts)
Output Signal의 magnitude가 2% 오차범위 이내로 Steady State Value와 가까워 졌을때를 의미하며,
이를 수식으로 쓰면 다음과 같이 정리될 수 있다.

즉,
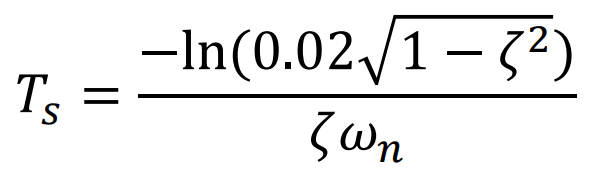
보통 이런 Settling Time은
시상수, Time Constant의 4배로 치는데,
Time Constant란, 간단하게말하면
System이 최종상태까지 1-e(-1) = 63% 까지 도달했을때의 시간을 의미하고,
이를통해서 아래와같이 정리할 수 있다.

이런 4가지 지표를 통해서 시스템의 거동을 판단할 수 있게되는데,
과도응답의 경우 다음과같이 생각할 수 있게된다.
○ Transient Response(과도응답) of System
과도응답이란, Steady State Response와 반대되는 개념이며,
시스템에 어떤 외부 인풋값이 들어갔을때 다시 Steady State해지기 전까지의 응답을 말한다.
시스템의 Transient Response는 다음과같은 두가지 Factor에 의해서 Measure해볼 수 있다.
1. Swiftness of Response : 얼마나 빠르게 Fv에 접근하는가? : Rise Time과 Peak Time로 표현
2. Closeness of Response : 얼마나 Fv와 가깝게 접근하는가? : Overshoot으로 표현
두가지 Factor,
Swiftness, Closeness는 서로 Trade Off관계로, 둘다 동시에 만족시킬 수 없는데,
Fv에 빠르게 접근하면, Overshoot이 커져서 Closeness를 만족시키지 못하고,
Closeness를 만족시키게 Overshoot이 작다면, Fv 에 빠르게 접근하지 못하여 Swiftness를 만족시키지 못한다.

○ Damping Ratio And Percent Overshoot (P.O), Peak Time (Tp)
Damping Ratio는 시스템을 해석함에 있어서 가장 많이 쓰이는 인덱스중 하나이다.
Percent Over shoot통해서 Damping Ratio를 Describe해보도록 하자. (별로 중요친 않은데 연습차원에서)
Output signal을 다음과같이 정의해보자

여기서 Peak Response는 다음과 같다.

이를 이용해 Percent Over Shoot을 구해보면

여기서 Percent Overshoot을 통해 Damping Rato를 계산해보면

○ Graph :: Tradeoff relationship between Swiftness and Closeness
위의 섹션에서
Damping Ratio를 이용해 Percent Overshoot을 표현할 수 있음을 설명했는데,
Peak Time인덱스 역시 Damping Ratio를 이용해서 아래와 같이 표현 가능하다

Percent Overshoot, 그리고 Peak Time 두가지 인덱스는
과도응답에서의 고려해야할 두가지 Factor인 Closeness, Swiftness와 각각 대응되며,
Trade off관계가 성립한다.
이에대한 그래프는 아래 그림과 같다.

Swiftness에 대해 Tp index 공식으로 조금더 이야기 해보면,
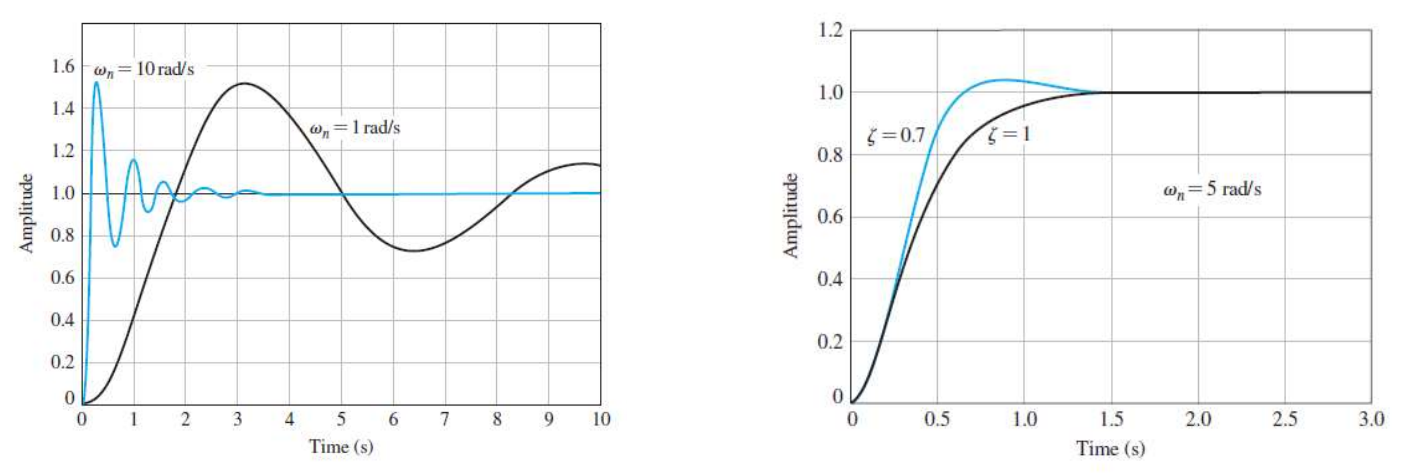
공식에서 Peak Time(Tp)을 결정하는 두가지 요인은 Natural Frequency와 Damping Ratio이다.
(이는 Rise time (Tr)도 마찬가지이다.)
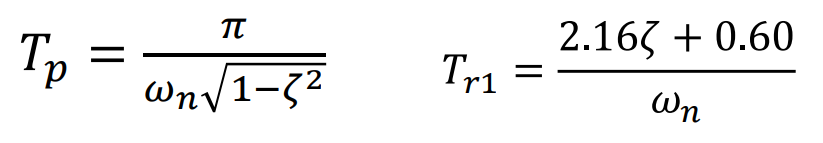
이 두가지 index에 대한 반응의 변화는 아래 그림과 같다.
◎ Pole Locations & Tp, P.O. , Ts
마지막으로, 중요한 부분을 다뤄보도록 하겠다.

Damping Ratio는 Pole이 이루는 각도의 cos, 즉 90도에서 0(Undamped)이며 0도에서 1(Critical Damping)이다.
Output Signal은 아래와 같이 정리된다.

x축을 Real Axis, y축을 Imaginary Axis로 설정한 아래와같은 좌표축에서,
시스템의 Pole의 위치를 결정할 수 있는데 이는 시스템을 해석함에 있어서 아주 중요한 부분이다.
(왜그런지는 추후 포스팅을 다루다보면 알게 된다...이후 나올 파트들이 다 이와 관련된 내용들이라...)


위의 그림처럼
Peak Time의 변화는 Imaginary 값에서의 변화를,
Settling Time의 변화는 Real 값에서의 변화를 의미하며,
Percent Overshoot의 변화는 Real Number와 Imaginary Number의 비율, 즉, 직선의 각도의 변화를 의미한다.
이에대한 수식적 설명은 다음과 같다.
먼저 Peak Time부터 살펴보면

여기서 Damped Frequency에 관련된 term으로 위의 식이 최종 정리되고,
이는 곧, System Pole의 Imaginary Part와 같다.
그렇기 때문에, Pole의 imaginary(y축)상의 변화를 일으킨다.
다음은 Settling Time이다

Settling Time을 묘사하는데 쓰이는 index는, Exponential Damping Frequency로 정리가되는데,
이는 곧 System Pole의 Real Part와 같다.
그렇기 때문에, Pole의 Real(x축)상의 변화를 일으킨다.
마지막으로 Percent Over Shoot이다

Peak time을 나타내는 index를 살표보면..
e의 지수에 붙어있는 값이 Peak time을 Settling Time으로 나눴을때 도출되는 값임을 확인할 수 있다.
즉, 이는 좌표축상의 Pole의 위치가 x축과 이루는 각도를 의미한다.
◎ Response & Pole Locations
우선 아래의 3가지 index에 대해 다음과같이 정리해볼 수 있다.

이런 수식을 이용해 Pole Location에 따른 시스템응답의 변화를 살펴보도록 하자
먼저 Imaginary Part 변화는 아래 그림처럼
y축과 평행하게 이동하는 것을 생각해 볼 수 있다.
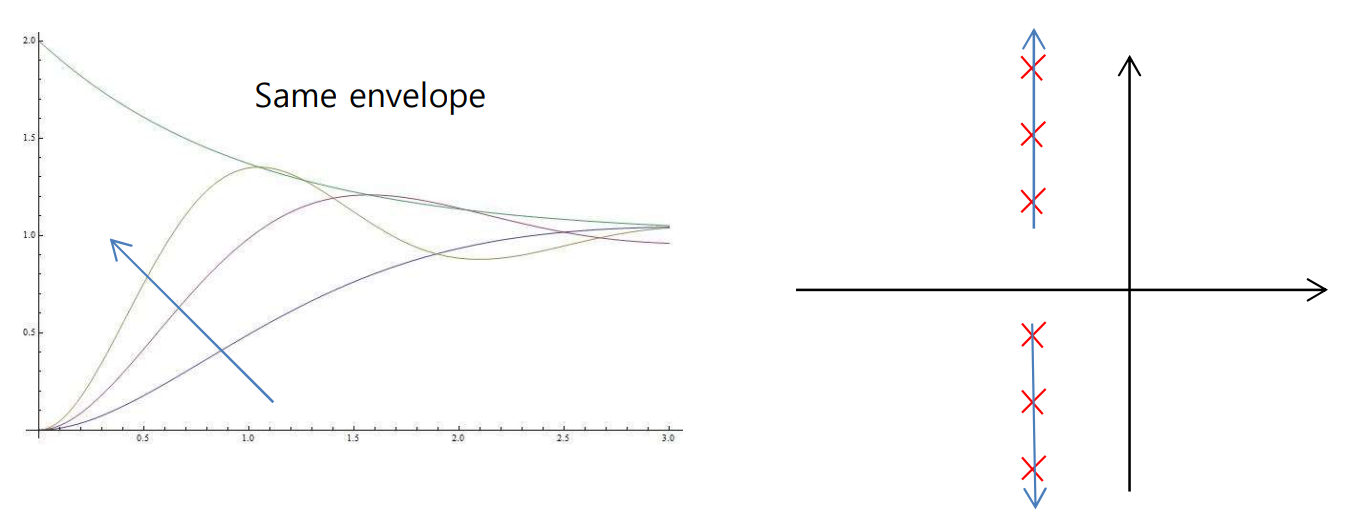
여기서 Envelope란, 진폭의 Boundary를 이야기하며, 자연상수 e의 계수가 이를 결정하는데,
이는 Real 값을 결정하는 인덱스, Exponential Damping Frequency이므로, Envelope는 Tp에 영향을 받지 않는다.
다만, imaginary값을 결정하는 인덱스인 Damped Frequency가 변화하므로, 아래와 같은 관계를 만족한다.

즉, Percent Overshoot과 Peak Time은 달라지는 것을 확인할 수 있다.
이번엔 Real Part 변화를 살펴보자.
아래의 그림처럼 x축에 평행하게 이동하는 것을 생각해 볼 수 있다.

imaginary Part를 결정하는 Damped Frequency가 일정하고,
Real Part를 결정하는 Exponential Damping Frequency가 변화하므로,
Peak Time은 일정하고, 나머지 두개의 index,
Settling time, Percent Over shoot은 영향을 받는다. 관계는 아래의 설명과 같다.

마지막으로,
Percent Overshoot에대해 살펴보자.
아래 그림처럼 생각해볼 수 있다.

Peak Time, Settling Time모두 변화하지만, Final Value값과 Overshoot이 일어나는 포인트는 변화하지 않는다.
즉, Percent Overshoot은 변화하지않는다.
이를
아래와 같이 정리해볼 수 있다.

지금까지 1차, 2차 시스템이 input에 어떻게 반응하는지에대한 해석을 여러가지 index를 통해 설명해보았다.
다음 포스팅에서는 2차 이상의 시스템, 즉 3개이상의 Pole이 시스템에 존재할때 이를 어떻게 해석할 수 있을지에 대한 방법에대해 다뤄보도록 하겠다.
'Control > 자동제어' 카테고리의 다른 글
| The Stability of Linear Feedback System (0) | 2021.11.23 |
|---|---|
| The Performance of Feedback Control Systems (2) (0) | 2021.11.13 |
| State Space Variables(2) (0) | 2021.10.17 |
| State Space Variables(1) (0) | 2021.10.16 |
| Mathematical Models of System(2) (0) | 2021.10.16 |




