정리노트
Mathematical Models of System(2) 본문
(1)에서 한 Component에대해서 어떻게 input output을 해석해야하는지 봤다면,
지금부터 전체 시스템에서 input, output을 어떻게 해석해야하는지 살펴본다고 생각하면 될것같다.
가장먼저 Transfer Function와 이를 통해 표시한 시스템해석예시를 가볍게 보고,
전체 시스템을 표현하는 Block Diagram, Signal Flow를 다루는 방법론에대해서 다뤄보도록 하겠다.
◆목차
◎ Transfer Function
◎ Transfer Function Examples
◎ Block Diagram
◎ Signal Flow
◎ Mason's signal Flow Gain Formula
◎ Examples
◎ Transfer Function
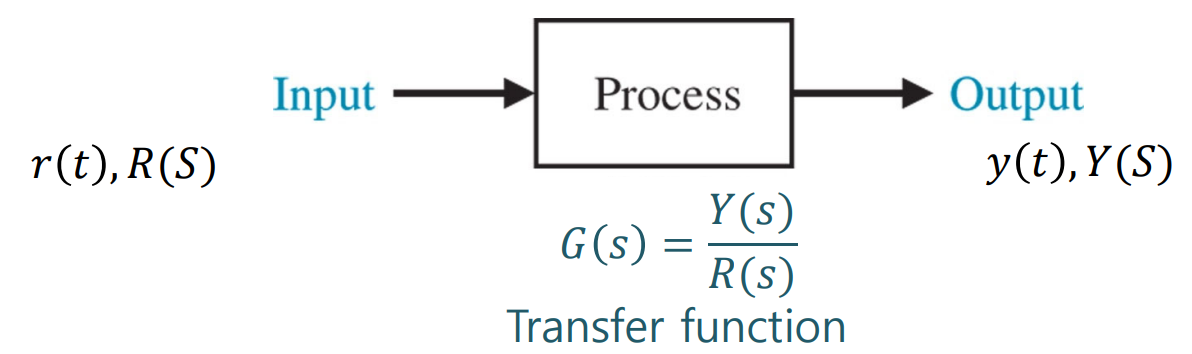
Transfer Function은, 쉽게말해 한 시스템이 들어온 input signal에대해 output signal을 어떻게 토해내는가에 대한 식을 나타낸 것으로, 그 시스템의 특성 그 자체라고 표현할 수 있다.

+@
Transfer Function은 Frequency 도메인에서 output signal/input signal로 정의된다.
이말인 즉, 만약 input signal이 Frequency 도메인에서 1, 즉 , impulse signal이라면,
Transfer Function은 곧 output signal과 같다.
이를 달리말하면 TF는 그 시스템의 impulse signal에대한 응답을 표현한식 이라고 생각할 수도 있는 것이다.
그래서 Transfer Function을 계산해주는 기계중에 망치처럼 생긴게 있는데...
그걸로 어떤 물체를 땅 두드리면 그게 곧 impuse 신호처럼 작용하여
System의 응답을 측정해 Transfer function을 계산해준다.

◎ Transfer Function Examples
○ RC Circuit
먼저 RC 회로부터 살펴보자.
여기서 시상수는 RC가된다.(이에대한 자세한 언급은 하지 않겠다)
RC Circuit에서 식을 보면, 어떤 input, output 물리량을 표현하는 Variable(위에서는 i,v)가 정해지고,
Block Diagram내에서 이에대한 식을 정리하여 output/ input 을 도출할 수 있으면,
우리는 이제 그 시스템 내부에서 어떤 일이 일어나는지 전혀 모르더라도
그 수식하나로 시스템을 해석할 수 있게된다.
○ OP Amp

전압차를 증폭시켜주는 OP Amp도, input과 output이 각각 Vin, Vo으로,
중간중간 각 signal간의 관계를 통해서 Transfer Function을 도출할 수 있다.
여기서, OP Amp는 Ideal 하다고 가정하는데, 다음과같은 조건을 만족한다.

위 가정을 토대로 아래 그림의 OP Amp 회로도를 해석해보자.

먼저 KCL적용

v1을 Vin이나, Vout으로 바꿔줘야 TF도출이 가능하다.
OP Amp의 Gain값은 아래 식을 만족하므로,


이를 이용해 정리하면



자, 여기서 gain값인 K는 충분히 크므로, 이를 아래처럼 정리가능하다.
즉, Transfer Function값... input대비 output출력을 R1, R2 저항값을통해 조절할 수 있는 것이다.
○ Multi input, Multi Output System..
만약 인풋 아웃풋이 여러개라면 어떻게될까?
보통의 시스템은 사실 인풋 아웃풋이 여러개 존재한다.
이럴때 보통 input, output Variable에대한 Matrix Notation을 적용하여 Governing Equation을 정리한다.
아래 예시를 통해 알아보자.

위의예시는 인풋은 r(t)로 하나, Output은 V1(t), V2(t)로 두개다.
각 Mass M1, M2에 대하여 Equation of Motion식을 세워보면

이를 라플라스 변환해보면

이를 보기좋게, 행렬로 변환해주자.
즉, input R(s)에대한 두개의 Transferfunction을 위의 식을 통해 구할 수 있다.
각각 V1(s)/R(s), V2(s)/R(s)를 해주면 된다.
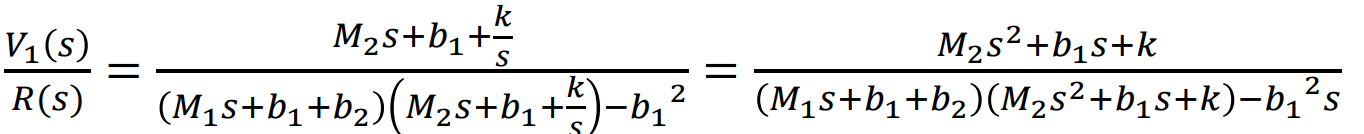
V2(s)/R(s)도 마찬가지..(생략)
◎ Block Diagram
시스템을 표현하는 가장 일반적이고 많이 쓰이는 표현방법이다.
Box 는 한 시스템을 표현, 즉, Transfer Function을 나타내며,
Box와 Box사이를 연결하는 화살표는 Signal이 된다.

Multi input, Multi Output 시스템의 경우,
보통 행렬로 시스템 식을 표현하는데, 이를 Block Diagram으로 Graphical하게 표현해보면

이런 Block Diagram는 아래처럼 응용될 수 있다.

곱에대해서 다음 분배법칙을 만족

즉,

도 만족.
제어 내내 지겹도록 보게될 Feed Back Loop도 하나로 합칠 수 있는데,
이건 Graphical한게 아니라 수식적인 정리를 한 것으로, 아래 내용은 하나의 포맷처럼 생각하여 접근한다.

G/1+GH .. 이 포맷은 정말정말 자주쓰이는 거니까 외워두자
이를 활용한 예제는 아래 그림과 같다

조금더 복잡한 예제를 풀어보자.
아래 그림과 같이 Overlap된 Loop의 경우 어떻게 해야할까?

여기서 앞서 봤던 Block Diagram의 응용을 이용하면,

이제 Feed Back Loop를 하나하나Elimination해보자.

최종적으로 정리해보자

여기서 계속 쓰이는건 G/1+GH 형식이다.
Negitive Feedback은 기계처럼 외워두도록 하자.
◎ Signal Flow
Block Diagram과 또 다른 한 시스템을 표기하는 방법으로,
책에 나온 표현을 빌리면
각 Variable당 interdependencies를 나타내는 Algebric Equation을 표현하는 Graphical한 방법이다
선형대수에서 중요하게 다루는 Graph와 깊은 연관이 있다.
Block Diagram에서는 Box가 TF, Box를 연결하는 화살표가 signal이었던 것과 반대로
Signal Flow에서는 각 Node가 Signal, Node를 연결하는 Branch(Edge)가 TF가 된다.
(이래서 ㅈㄴ헷갈린ㄷ)


연산은 Block Diagram과 마찬가지로, 직렬일때 더하고 한노드에 여러개의 Branch가 들어오면 더하면된다.
Signal Flow도 각 노드를 합칠 수 있는 경우가 있는데, 아래 예제를 통해 자세히 살펴보자.

위 Block Diagram에서.. 우선 각 Signal당 노드를 그려보자

이를 이어주면
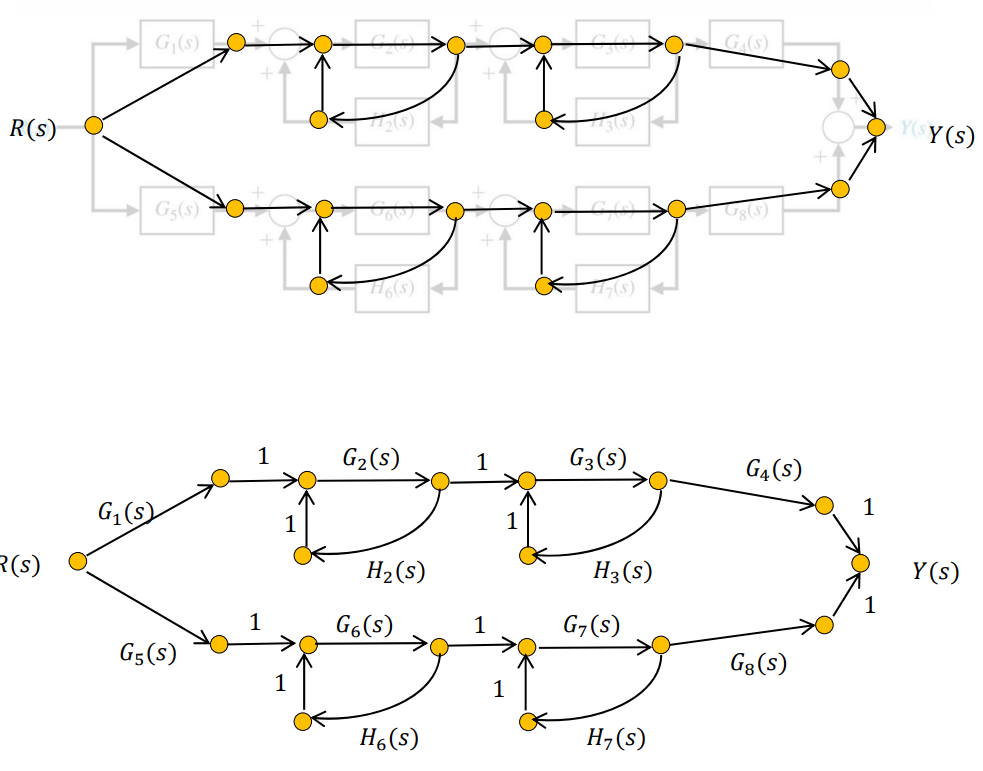
각 Transfer Function을 기입해주면 위와같은 그림이 된다.
여기서, 한번더 단순화 시킬 수 있는데 조심해야할 포인트가 한가지 있다.

... 가운데 노드가 합쳐지면 안되는 명확한 근거는 솔직히 아직 못찾았다
(다른책에서 signal이 같을때만 합칠수 있다고 하는데 이 논리는 반박가능한 부분이 있어서... 명확해지면 추후 정리해서 올리겠다.)
이에 대한 이야기는 ◎ Examples에서 다뤄보도록하고,
Signal Flow이야기로 돌아오자. signal Flow에서는 Transfer function을 어떻게 구할까?
이에대한 기본적인 아이디어를 얻기위해 아래 그림을 살펴보자

정리하면

TF를 계산하기위해 아래처럼 정리해보자

위에서와 마찬가지로,


여기서 Crammer's Rule를 적용하면

뭔가 Cofactor, Determinant와 깊은연관이 있다고 추측해볼 수 있다


자, 여기까지 정리한 상태로,
signal Flow에서 TF를 구하는 방식인 Mason's signal Flow Gain Formula에 대해서 이제 본격적으로 다뤄보자
◎ Mason's signal Flow Gain Formula
Mason's signal Flow Gain Formula는
Signal Flow에서 두 노드 Xi, Xj사이간 Transfer function을 구하는 Formula로, 공식은 아래와 같다

각 텀이 의미하는 내용은

Gain값, 그리고 루프와 Path간 Touch/Nontouch여부에 따라서 각 텀들이 달라진다.
조금더 자세히 알아보자.
Graph의 Determinant는


Path의 Cofactor은

즉, 해당 Path와 Touching Loop Gain을 Determinant식에서 0으로 만들면
Path의 Cofactor을 구할 수있다.
예제를 통해 자세히 알아보자.

2개의 Path :
P1 = G1*G2*G3*G4
P2 = G5*G6*G7*G8
4개의 Loops

그중 Nontouching Combination은
L1, L2, L3, L4
L1L3, L1L4, L2L3, L2L4
3개 조합 부턴 존재하지않는다.
즉, Determinant는
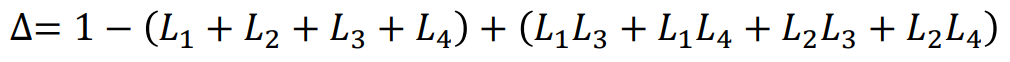
Cofactor는 위 Determinant식에서 해당 Path의 Touch Loop Gain값만 0으로 넣으면된다.


◎ Examples
○아까전 합치면 안됐던 문제
우선 아까 signal Flow그래프에서 같으면 합치면 안되는 노드에대해서 다시 살펴보도록하자.
Block Diagram에서 도출해낸 TF와 Signal Flow에서 도출해낸 TF를 비교해보면 확실히 합치면 안되는게 맞다는걸 알 수 있다.
......책이 틀렸을 거라고는 생각 하지않아서.. 교수님이 잘못 착각하셨겠거니 했는데
아래그림을보고 납득해버렸다..
..맨 위에 Block Diagram에서 왼쪽이 교수님께서 그린 SignalFlow이고, 오른쪽이 Modern Control System 12판에 나온 그림이다.

두 Path중 윗부분만 떼어놓고 생각해보면,
맨 위의 Block Diagram에서 Transfer Function과, 책에 나온 오른쪽 아래 Transfer Function의 결과값이 다르다..
그리고 가운데 Touching Node를 분리해서 생각한 왼쪽 아래의 Transfer Function과 답이 같다.
일단 여기까지 알아두고 명확한 기준이 제시될때 이글을 한번더 수정해보도록 하겠다.
○ Armature DC Motor





비교적 심플하다(아마도)
○ Multi Loop System Example1

위와같은 Block Diagram에서,
Block Diagram의 접근법상 아무런 변환없이 그대로 TF를 계산하는 것은 불가능하다
이를 Signal Flow적인 해석방법으로, Mason's Formula를 바로 적용해서 TF를 계산하면,
별도의 변환없이도 TF계산이 가능하다.
Path는 한개, Loop는 3개인 Signal Flow로 생각하면

○ Multi Loop System Example2
그냥 Mason's Rule.. 극한의 연습용으로,
시간있으면 한번 풀어보면 좋다.. (이렇게까지 복잡한 시스템을 쓸일이 있을까 싶ㄷ)


-> Path갯수 증가






이상 Mathematical Models of System 장에대한 이론적인 부분은 마친다.
따로 정리해보고 싶은 예제는 Example 글을따로 포스팅하며 다뤄보겠다.
'Control > 자동제어' 카테고리의 다른 글
| State Space Variables(2) (0) | 2021.10.17 |
|---|---|
| State Space Variables(1) (0) | 2021.10.16 |
| Mathematical Models of System(1) (0) | 2021.10.15 |
| Laplace Transform 정리(2) (0) | 2021.10.12 |
| Laplace Transform 정리(1) (0) | 2021.10.12 |




