정리노트
Mathematical Models of System(1) 본문
지금까지 시스템을 컨트롤 하는게 무엇이며,
어떻게 해석해야 하는지에대한 기초 방법으로 Laplace Transformation을 비교적(?) 자세히 다뤄보았다.
이번 글에서는 Laplace의 Application에대한 전체 과정을 다뤄보고자 한다.
먼저 라플라스에대해서 간단하게 짚고,
Mechanical, Electrical 시스템을 모델링 (ODE만들기),
테일러급수에서의 Linearization, Solving ODE를 풀텐데
Damping ratio에 따라서 ODE해석을 어떻게 달리할 수 있는지에대해 자세히 알아보도록 하겠다.
◆목차
◎ Laplace Transform Summary
◎ System modeling of Mechanical System & Electrical System
◎ Linear Approximation (Linearization)
◎ Solving ODE(Ordinary Differential Equation)★
◎ Laplace Transform Summary
-> Definition of LT, & ILT
LT : t->s


-> Existency

-> Table

-> Properties

◎ System modeling of Mechanical System & Electrical System
시스템이란, 여러 물리적인 Component들이 모여서 input에대한 특정 output을 반환하는 하나의 집합?
이라고 생각해보면 될 것이다.
시스템을 해석한다는 것은,
시스템을 구성하는 각 Component들이 input에대한 output을 어떻게 반환하는지(T.F)
그리고 Component들이 하나로 뭉쳤을때 input에대한 output반환을 어떻게 Equivalent하게 해석하느냐에 관한 내용이다.
물리계중,
가장 흔하고 대표적으로 다루는 두가지는 Mechanical System, Electircal System이다.
먼저 가장 흔하게 알려진 Mechanical System부터 살펴보도록 하자
○ Mechanical System

각 force의 차원
중력(mass) : y''
마찰력(damping) : y'
탄성력(spring) : y
m*y'' + b*y' + k*y = f
input : f
output : y

mbk Mechanical System의 ODE를 깔끔하게 구했다.
Derivation에 관한 Laplace 변환을 적용하여 r(t)-> R(s), y(t) -> y(s)로 라플라스 변환을 해주고,
output/ input, 즉 한 시스템 계를 표현해주는 Transfer Function을 구하면 된다.
이에대한 자세한 내용은 Inverse Laplace부분에서 다루겠다.
○Electric System
Electric System에대한 ODE도 세워보자.
RLC Circuit 의 System 모델링 식은 mck Mechanical System 모델링 식과 Equivalent한 것으로 많이 알려져있다.
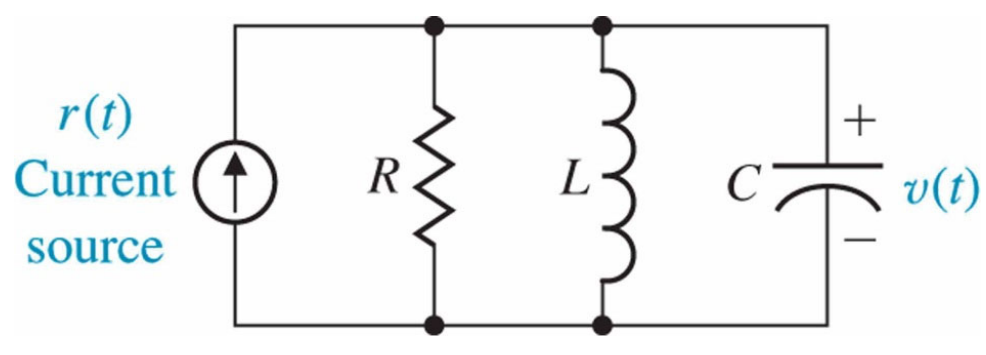
Electrical System의 각 component.. R(저항), L(인덕턴스), C(커패시턴스)에대해서 조금 자세히 들여다보면

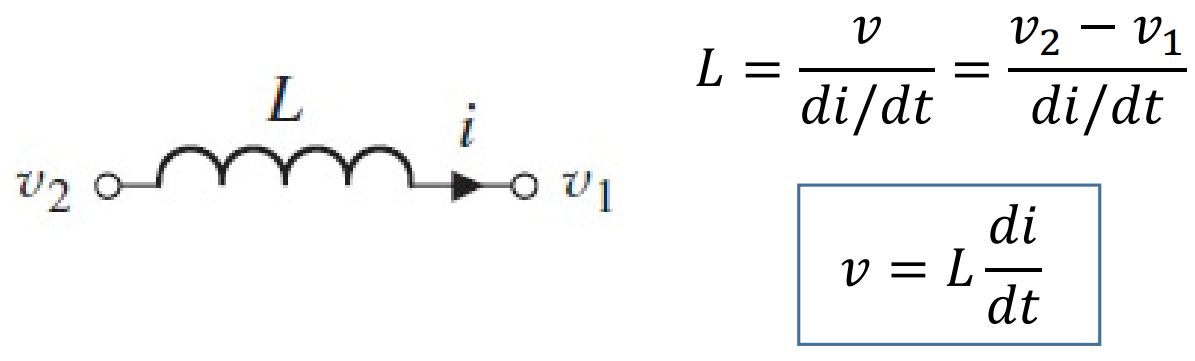

+@ Stored Energy

Electrical System에서, 키르히호프 전류법칙을 적용해서 식을 정리하면..
(Current Source에서 나오는 전류r(t)대비 output전압 v(t)으로 정리한 식....
그 반대도 가능하다. input이 전압, output이 전류일 수도 있다.. (직렬로 연결))

◎ Linear Approximation (Linearization)
'Linearity' 는 보통 아래 두가지 특성을 만족한다
1, Superposition

2, Homogeneity

즉, 간단하게 서술하면 '곱과 합에대해서 닫혀있다' 생각하면 된다.
Note -> y(x) = Mx+b => (b=0이 아니라면) Nonlinear System
Linearization이란, Nonlinear Equation을 Linear하게 Approximation해주는 것을 의미한다.
이런 Approximation이 필요한 이유는, Nonlinear System을 해결하는게 더 복잡하고, 해를 도출하기 어렵기 때문이다.
Linearization에는 Taylor Expansion이 사용된다.


...쉽게말하면 그냥 접선이다
Multi Variavle Function .... input, output이 여러개 존재하는 시스템의 경우,
각 Variable 단위로 Linearization을 진행해 줄 수 있다.
○ Simple Example of Linearization : Pendulum Oscillator



가장 대표적인 예시라고 볼 수 있다.
◎ Solving ODE(Ordinary Differential Equation)
이제 ODE를 풀기위한 모든 준비를 마쳤다.
지금부터 Laplace Transform을 활용하여, 모델링한 ODE를 통해 한 시스템안에서 어떻게 output Signal이 나오는지 살펴보고, 어떻게 해석하는지 알아보도록 하자.

지겹도록 본 mbk System모델링 식을 Laplace변환해보자.
만약 외부에서 별도의 input이 없고, 초기 위치값만 y0인 시스템이면 (y'은 0)


위의 식에서 분자의 근과 분모의 근은 각각 Bode Plot에서 Pole, Zero가 되며,
분모의 방정식 = 0은 특성방정식(Characteristic Equation)이라고 불린다.
즉, S Domain에서 표현된 output signal으로,
지금 시스템이 어떤 특성을 띄고있는지 Characteristic Equation을 통해서 알 수 있는것이다.
단순한 예시를 통해 자세히 알아보자.
Example)



inverse Laplace Transform을 해주면

Note Point : 여기서 분모의 근 : -1. -2는 y(t)가 얼마나 빠르게 0으로 수렴할지 결정함
+ 여기서 Laplace Transform에서 정리했던 Final Value Therom을 적용시켜봄으로서, State State(t가 충분한 시간이 흘렀을때)에서의 값을 도출해보면

○ General Representation of the System
위에서 기본적인 예시를 통해 시스템을 어떻게 바라보는지에대해서 간단하게 살펴봤다.
지금부터 조금 시스템 해석에 관해서 General한 Notation에대해 정리해보도록 하겠다.

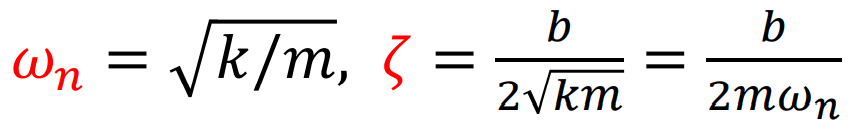

여기서 특성 방정식의 근은 다음과 같다.

특성방정식의 해에서, 두가지 파라미터 Damping ratio, Natural Frequency가 있는데,
Damping ratio 값에 따라서,
해가 허근, 중근, 두 실근을 가질지 결정된다.
이는 곧, damping ratio에 따라서 시스템이 input에대한 응답을 어떻게 토해내는지 파악할 수 있는 것이다.
지금부터 특성방정식이 허근, 중근, 실근을 가질때 시스템은 어떤 반응을 하는지 살펴보도록 하자.
* Damping ration는 댐핑의 정도를 나타낸다.

○ Undamped

Damping이 없기에 진동이 보존된다. 이를 직접 넣어보면

Wn은 Natural Frequency로 고유진동수에 해당한다.
○ Underdamped



이 Output Signal을 정리헤보면,

여기서, undamped Natural Frequency를 다음과같이 정의해보자

그리고, Lapace transform에서 우리가 잘 아는

이 식을 생각해보며 정리해보면,
한번더 위의 Output Signal을 간단하게(??)만듪 수 있다.

자. 여기서 심호흡 한번하고,
e^(-at)sin(wt), 또는 e^(-at)cos(wt)로 바꿔보면


즉, tan의 결과를 특정 각도 theta라고 할때
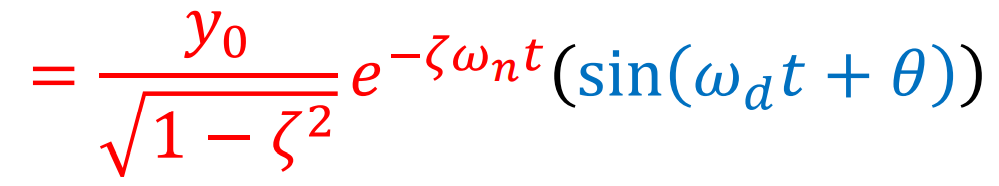
Damping Ratio에 따른 감쇠 그래프를 그려보면

그냥 상식적인선에서 생각을 해보면, 질량대비 Spring상수 K에 대해서, Damping이 클수록 더 빠르게 진동이 감쇠하는 것이라고 볼 수 있다.
○ Overdamping


특성 방정식이 실근을 가지고 있으니, 허근을 가졌을 때 처럼 분모가 이상하진 않다..
(그래도 복잡한건 똑같다 ..)
다시한번 심호흡하고 Overdamping일때 output signal 식을 정리해보면....




식은 복잡했지만 어찌저찌됐건 Residue가 Coefficient가 되며,
y가 0보다 작아지지 않으므로, 진동은 일어나지 않는다.
단, 수렴하는데 까지 걸리는 시간이 더 걸린다. 그래서 Overdamping이라고 할 수 있다.

○ Critical Damping
제어에서 Overdamping과 Underdamping 사이, 가장 이상적인 제어상태라고 볼 수 있다.
특성방정식이 중근을 가지는 상황으로 진동이 없으면서도 가장 빠르게 수렴상태로 도달한다.
우리가 제어를 하려면, 이 Critical Damping한 상황으로 시스템을 조절할 수 있어야한다.


이때 특성방정식의 중근은 시스템의 Natural Frequency값과 같게된다.



지금까지 내용을
Summary 해보면 다음과 같다.

글이 너무 길어졌다. 이에대한 자세한내용은 일단 여기서는 다루지 않고
추후 시간이 나면 따로 다루도록 해보겠다
'Control > 자동제어' 카테고리의 다른 글
| State Space Variables(1) (0) | 2021.10.16 |
|---|---|
| Mathematical Models of System(2) (0) | 2021.10.16 |
| Laplace Transform 정리(2) (0) | 2021.10.12 |
| Laplace Transform 정리(1) (0) | 2021.10.12 |
| Control System_ introduction (1) | 2021.10.12 |




