Laplace Transform 정리(2)

지금부터는 Laplace의 이론적인 내용에 대한 설명이다.

(1)포스팅에서 ODE를 Laplace 해석으로 어떻게 간단하게 풀리는지는

Mathematical Models of  System 포스팅에서 다루도록 하겠다.

 

◆ 목차

◎ Definition of Laplace Transform

◎ Exisitence of LT

◎ Linearity

◎ s - shifting /  t - Shifting

◎ Laplace Table

◎ Derivative / Integral 에대한 Laplace해석

◎ ...대표적인 예시 : Unit Step Function(Heaciside function)에대한 Laplace해석

◎ +@ Final Value Therom , Initial Value Therom, 

 

 

 

◎ Definition of Laplace Transform

t -> s Domain으로 전환하는 

Laplace Transform의 정의는 다음과 같다.

(t >0.. 0이 포함 될수도있고 안될수도 있는데 existence부분에서 가볍게 다루겠다)

부분적분법 공식

 

이를 푸는 것은, 보통 부분적분법을 이용한다

 

                                                                          부분적분법 공식:

 

 

 

 

예시를 통해 살펴보자.

 

 

 

  step function의 L.T

 

 

Exponential Function의 L.T

 

 

sin/cos Function의 L.T

 

 

 

복잡해보이지만,

부분적분법을 통해 따라가다보면 크게 어렵지 않게 풀린다.

 

위의 정의를 통해 기본적인 Function들의 laplace Tranformation Table을 작성해보면.. 

기본적인 input funtion의 Laplce Function Table

 

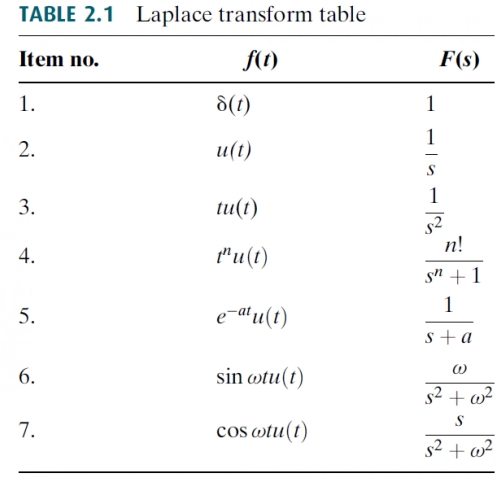
t -> s로의 전환을 Laplace Transform, 줄여서 L.T... 그와 반대인

s -> t로의 전환을 Inverse Laplace Transform, 줄여서 I.L.T라고 한다.

 

Laplace의 장점은,

Function의 Laplace Table만 가지고 있다면, 어떤 ODE건 손쉽게 풀수 있다는 점이다.

(그리고 공업수학에서 ODE Solution을 구하는 과정처럼 Assumption에 의존하여 푸는 것도 아니다.)

 

 

◎ Exisitence of LT

Laplace의 존재조건은, Laplace계산과정에서 부분적분을 할때, 

(t -> 무한대)에서,  e^(st)와 f(t)의 계산이 이루어지는 과정중

이 Exponential 함수가 어떻게 결정될 것인지에 따라 달렸다.

 

계수가 -무한대 또는 +무한대로 갈텐데, exponential 함수에서 수렴조건에 따라,

-무한대로 계수가 이동하는지 따져주면 되는 것이다.

 

 

여기서, 한가지 더 따져주어야하는 포인트가 있는데

변환의 경계값인 t =0을 포함 시켜야 하는가에대한 내용이다.

 

+ 이에대한 수렴조건을 따지는게 

사실 시스템 모델링에서는 크게 의미가 없는게 f(t)자체가 Finite한 함수를 다루기 때문이다.

f(t) 가 Infinite한경우, 수렴조건이 조금 복잡해지게된다

여기선 간단하게 t = 0일때만 짚고 넘어가보도록 하겠다.

 

답은 간단하다 f(0)이 무한대로 발산하면 라플라스는 존재하지 않으며,

finite 한 특정값을 가지는 경우 수렴한다.

 

◎ Linearity 

Laplace Transform은 선형성을 만족한다.

 -> 곱과 덧셈에 대해 닫혀있다.

('선형성'의 정의에 대해서 자세히 언급하진 않겠다.)

 

증명은 정의에서 간단하게 도출가능

 

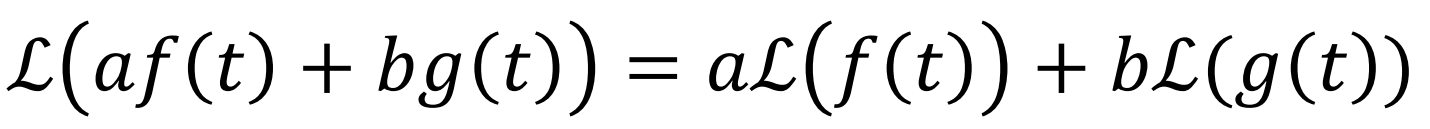
◎ s - shifting /  t - Shifting

 

  ○ s -shifting

먼저 s shifting부터 살펴보자. 

간단하게 말해서 s Domain에서 shifting, 즉 평행이동하면 t Domain에서 어떤 변화가 있을 것인가?

에 대한 내용이다.

 

Laplace의 정의에 의해서 다음과 같은 식이 성립된다.

Laplace의 정의로부터, 자명하게 도출할 수 있다.

 

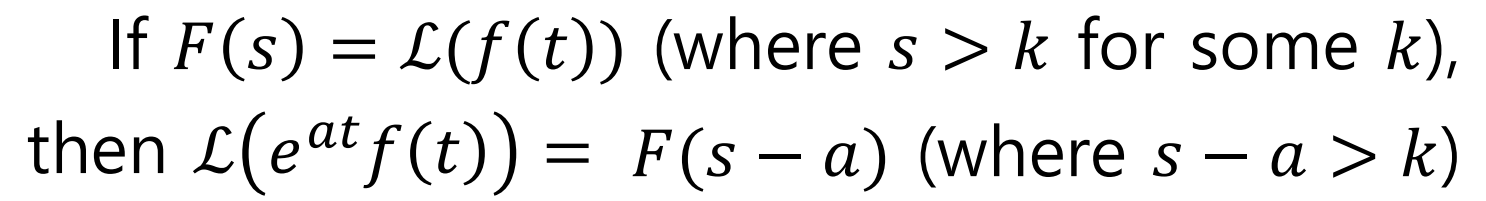
진동에서 s-Shifiting 예)

그외 예)

 

 

 

 

 

 

 

 

 

 

 

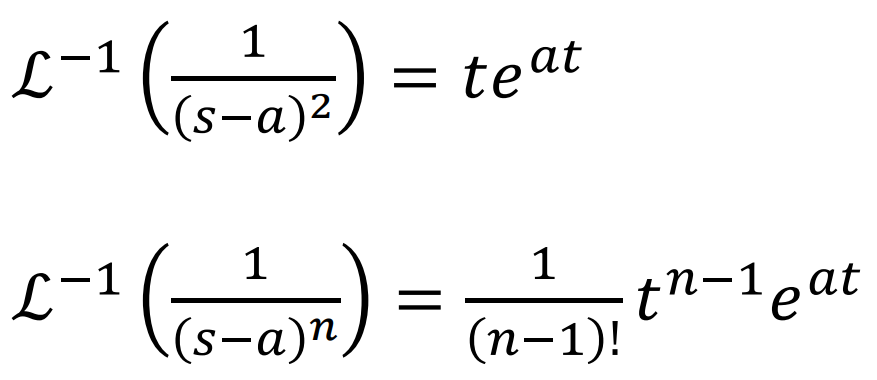
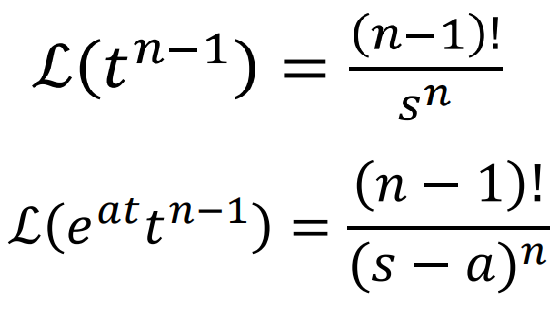
  ○ t -shifting

 반대로, t Domain에서 평행이동이 s domain에서 어떤 변화를 불러일으킬지 보면 된다.

아래 그림을 통해 살펴보자.

함수 f의 shifted function을 다음과같이 정의함

이때 f의 shift는 아래 그림과 같이 정의가 된다.

왜일까? 

e^(-as)가 곱해진것이 왜 s Shift일까?

증명은 다음과 같다.

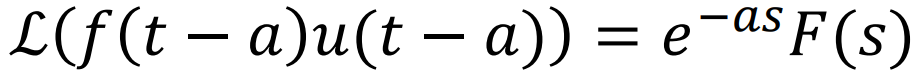
이유는 생각보다 단순하다

 

 

 

 

 

 

 

 

 

 

 

 

 

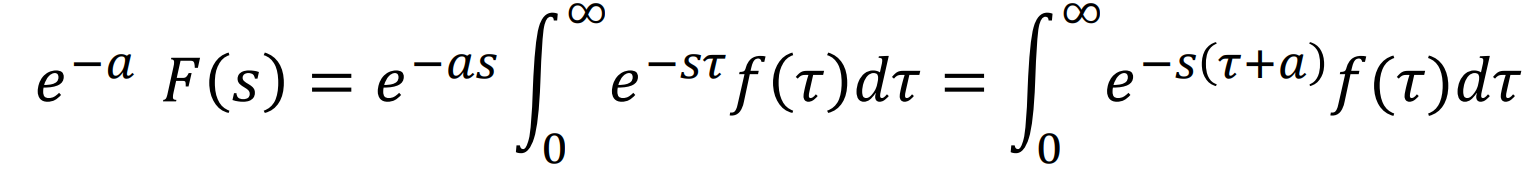
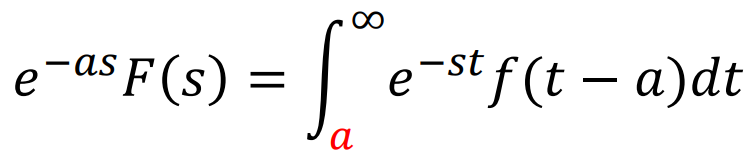
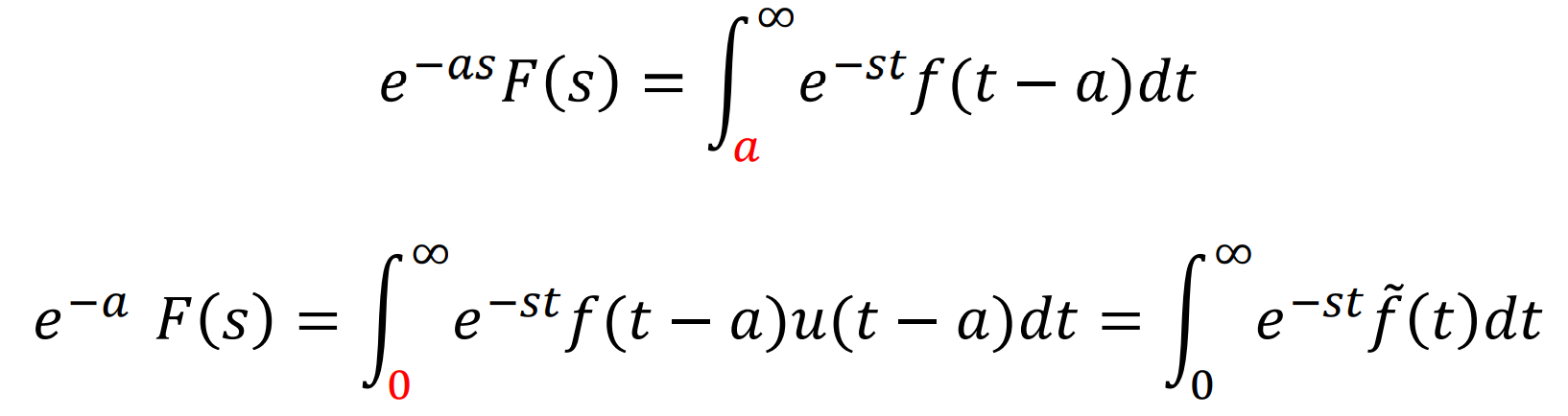
◎ Derivative / Integral 에대한 Laplace해석

 

지겨운 이론파트가 거의 끝나간다.

조금만 힘내자.

 

Derivative, Integral에 대한 Laplace해석도 앞선 과정들과 마찬가지로 중요하다.

모든 Laplace가 그렇지만 사실 유도과정이 그렇게 크게 중요하지 않다.

결론만 알고 써도 아무런 문제가 없지만 이왕 정리하는김에 한번 간단하게라도 유도해보도록 하자.

 

 ○ Derivative

2차 시스템까지의 laplace해석

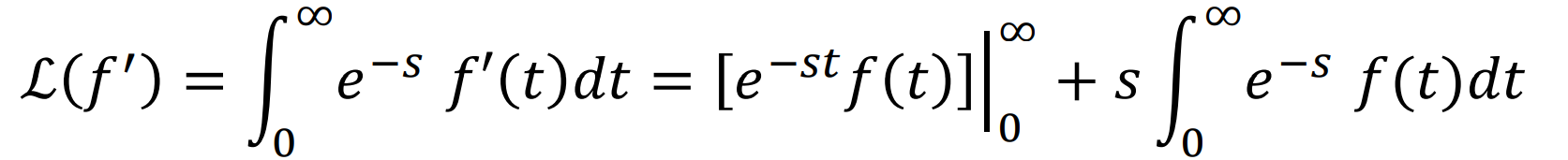
2차 미분도 1차미분의 결과를 한번더 미분함으로서 유도가 가능하다.

 

 

 

즉, General한 n차 미분에대한 Laplace 해석을 써보면,

 

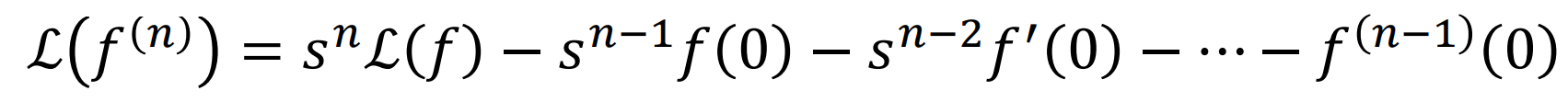
 ○ Integral

Derivation을 이해했다면,

Integral도 쉽게 유도할 수 있다.

g를 f에대한 적분이라고 해보자

정의에 의해서,

 

즉, 적분의 결과는 

미분의 결과는 s를 곱하는 것.

적분의 결과는 1/s를 곱하는게 다르며,

적분은 초기값을 생각안해도 되지만, 미분은 초기값을 생각해야하는점도 다르다.

 

 

 

◎ ...Laplace Example : Unit Step Function(Heaciside function)에대한 Laplace해석

step Function의 모습이다. 정말 흔하게 많이 쓰이는 함수다.

 

time shifting된 형태의 step function

 

위의 방법을 써도 되고,

또는 t- shifting의 정의에 의해서, L(u(t))의 결과(1/s)에 e^(-as)한 것이라 생각해도 된다.

◎ +@ Final Value Therom , Initial Value Therom

 

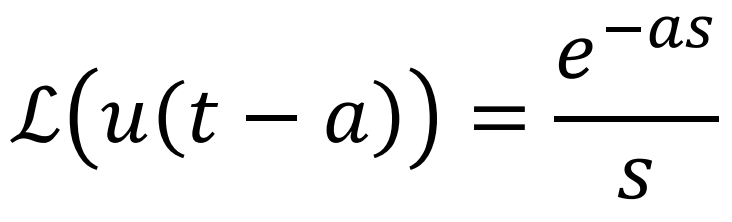
Final Value Therom

 

 

 

 

 

 

 

 

 

 

 

Initial Value Therom

 

 

 

 

 

 

 

 

 

 

 

 

 

 

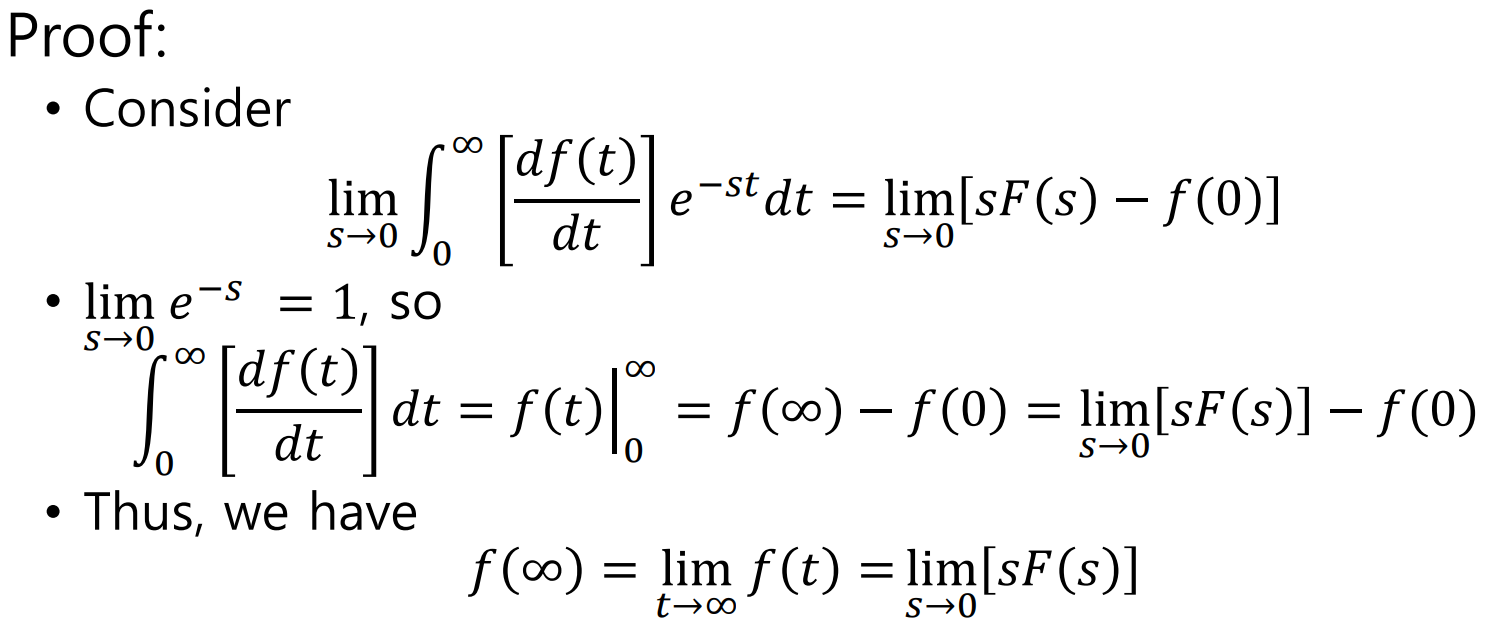
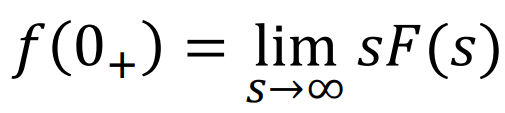
  조금 쉽게 이를 생각하면, t가 무한대로 갈때 s도메인에서 s는 0으로 가는 것과 Equivalent하며,

 반대로 t가 0+로 접근하면, s는 무한대로 가는것과 Equivalent하다는 것이다.

 

 

 

 

 

 

 

여기까지가 Control System을 이해하는데 필요한 Laplace Transform의 전반적인 내용이었다.

이제 다음 글부터 본격적인 System에 대한 Mathematical Model을 해석하고, 컨트롤하는 방법에 대한 부분을 다뤄보겠다.