정리노트
Deep Learning (2)_ Shallow Neural network 본문
지난 포스팅에서 Neural Network에서 한개의 노드구조에 해당하는 Linear Regression과 그에 sigmoid Function이 합쳐진 Logistic Regression을 살펴보았다.
이런 Perceptron을 층층이 겹쳐올린 구조로 학습을 하는 모델을 Neural Network라고 하는데,
층의 깊이가 깊지않은 모델을 Shallow Neural Network, 깊은구조를 Deep Neural Network라고 한다.
이번 포스팅에서는 층의 깊이가 깊지않은 Shallow Neural Network모델 중 가장 단순한 모델인
MLP(Multi Layer Perceptron)에 대해 다뤄보도록 하겠다
*코드첨부는 맨 아래 쪽에
◆목차
◎ Neuron의 구조
◎ XOR Operator Issue (Decision Boundary of Logistic Regression)
◎ Neural Network with Hidden Layer (ex. MLP)
◎ Activation Functions
○ Why Activation Functions are Non-Linear Function?
○ Gradient Vanishing/Exploding/Knock out
◎ Process of G.D in MLP
◎ Neuron의 구조
Neuron의 구조는 아래와 같다.

이전 Layer Node의 Output, 혹은 모델자체의 input을
Linear Regression 모델 W*X+b의 input으로 넣고,
그 Value를 Activaion Function에 한번 통과시킨 값을 다음 Layer의 Neuron에 Propagation한다.
이를 그림으로 표현하면 아래의 예시처럼 표현가능하다.

◎ XOR Operator Issue (Decision Boundary of Logistic Regression)
Logistic Regression에서 Neural Network로 넘어갈때 대표적으로 다루는 예시인데,
Feature가 두개이고, 각 Feature의 Value가 0 또는 1로 구성되어있는 데이터셋이 있다고 하자.
-> Sample Space는 (0,0),(0,1),(1,0),(1,1) -> label은 Operation에 따라 0또는 1
이 데이터셋으로 그래프상에 And, Or, Xor 연산을 표현할 수 있는데

-> And, Or은 구현할 수 있겠는데, Xor 연산자는 Logistic Regression로 구현이 가능한가?
앞전 포스팅에서 Logistic Regression에서의 Decision Boundary는 Sigmoid Function의 Output이 0.5가 되는 지점, 즉, W*X+ b = 0이되는 지점이라고 언급하였었다.

Linear 한 W*X+b = 0 Subspace를 기준으로 Classification을 진행하는 것을 Logistic Regression이라고 하며,
이때 W*X+b=0 Subspace를 Decision Boundary라고 한다.
And, Or, Xor 그림과 아래 그림에서 볼 수 있듯이,
Linear한 Decision Boundary하나로 And, Or 의Classification은 가능하지만,
XOR의 Classification은 한개의 Linear Decision Boundary로는 불가능 하다는 것을 알 수 있다.


이에 대한 자세한 내용은 포스팅 끝부분에 코드로 첨부해둘테니,
Jupyter Notebook상에서 한번 확인해보면 좋을듯 하다.
◎ Neural Network With Hidden Layers (ex. MLP)
Neural Network를 이루고있는 Layer의 종류는 크게 3가지로,
Input Layers, Hidden Layers, Output Layers이다.

Input Layer은 데이터의 input값을 input으로 받아들이는 Layer이고,
Output Layer은 모델의 최종 Output을 토해내는 Layer이며,
그 사이 연결되는 모든 Layer를 Hidden Layer이라고 한다.
MLP의 구조는 아래이 input Layer와 Output Layer사이에 한개의 Hidden Layer로 이루어진 구조이다.

* 참고
Hidden Layer의 노드의 개수는 Input Feature개수보다 많거나 작을 수는 있지만,
input Feature에 비해서 너무 많은 수의 Hidden 노드를 사용해서는 안되고,
데이터 수가 작을 수록 간단한 구조를 채택해서 사용해야한다. (일반적으로)
수식표현을 이어서 해보면
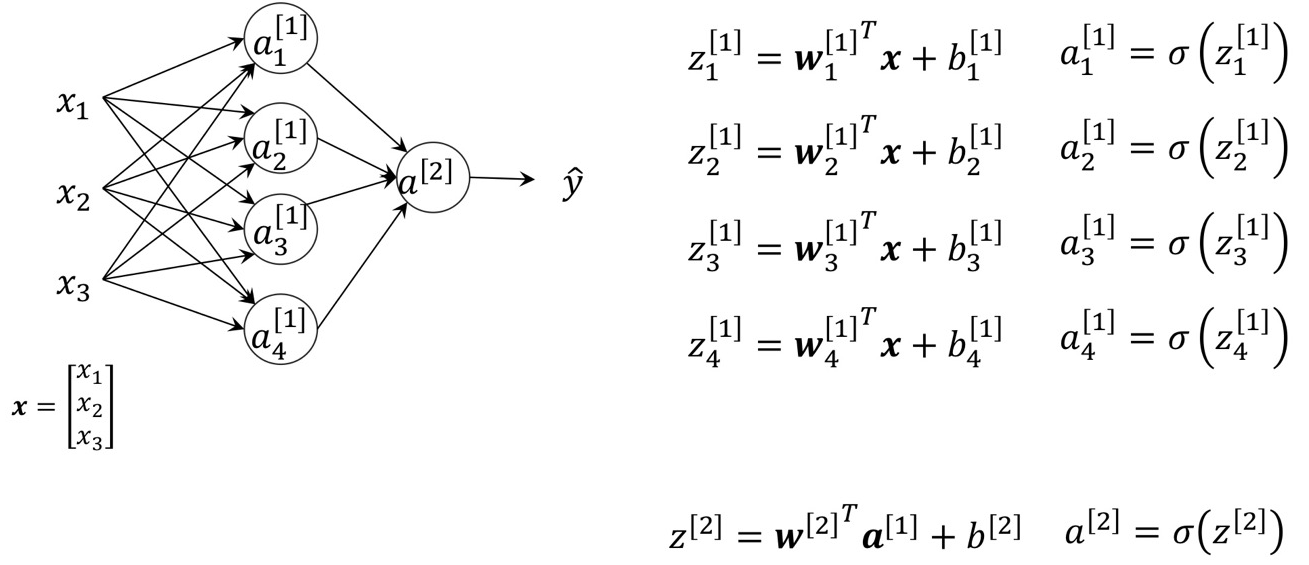
정리하면

◎ Activation Functions
Neural Network의 각 노드의 구조는 Linear Regression에 Activation Function을 통과하는 구조라고 하였다.
이때 Activation Function의 종류는 아래 그림에서 알 수있듯 정말 많은데,

다 알필요는 없고, 99.9% 이상의 Nerual Network에서는
Sigmoid, Tanh, ReLU, LeakyReLU 정도의 Activation Function을 사용한다.
아래 내용들은 각 Activation Function에대한 설명이니 한번 참조
- Sigmoid

- Hyperbolic Tangent: Tanh

- Rectified Linear Unit (ReLU)

- Leaky ReLU
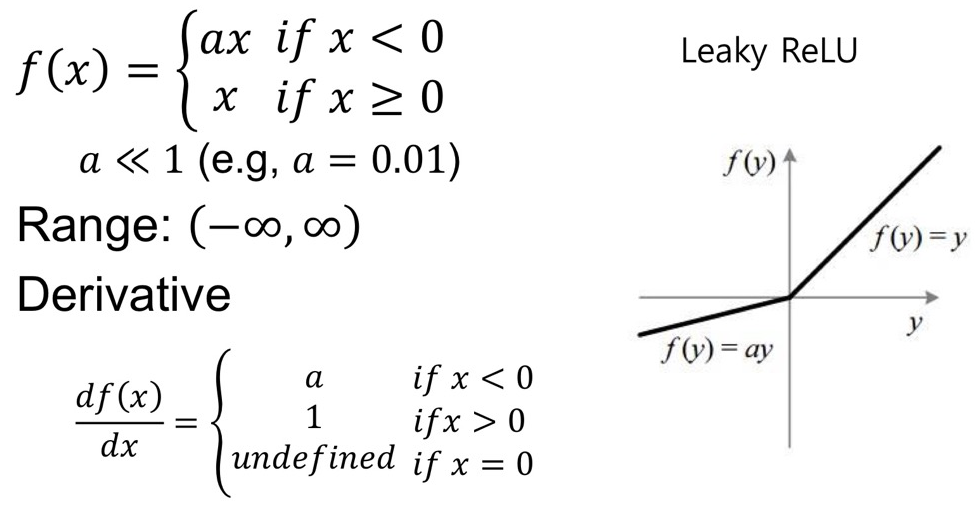
○ Why Activation Functions are Non-Linear Function?
위의 4가지 Activation Function을 살펴보면 알겠지만, 모두 Non-Linear한 Function이다.
왜 Linear한 Activation Function을 안쓰는 걸까?
여러차례 이야기 했듯이, Neural Network에서 하나의 노드는 Linear Regression의 출력값을 Activation Function에 통과시키는 구조라고 하였다.
즉, Activation에 통과시키기전의 모델은 데이터의 'Linear한 관계'를 예측하는 모델이다.
Activation Function이 Linear하다는 것은, Linear한 관계를 예측하는 모델에 Linear 한 함수를 통과시킨 것으로
사실상 Activation Function이 있으나 마나 하게 된다. (그저 크기를 키우고 늘이고 밖에 할수 없기 때문에)
만약 Activation Function이 Linear하다면, Network의 층구조는 그 의미를 잃는다.
Linear Layer가 1개있으나,10개있으나, 100개있으나.. 같은 기능을 하는 Linear Layer하나로 정리가 가능하다.

2개의 Layer구조인 위 그림으로 이를 증명할 수 있다.
○ Gradient Vanishing/Exploding/Knock out
위에서 언급한 Activation Function은 4가지.
Sigmoid, Tanh, ReLU, Leaky ReLU이다.
보통 Deep한 Neural Network로 갈 수록 ReLU를 사용하는데,
-> Sigmoid나 Tanh에서 발생하는 "Gradient Vanishing"
: 기울기 값이 1보다 작아서, Back Propagation의 Chain Rule을 적용하는 과정 중 Gradient가 0으로 소실되는 현상)
->혹은 (여타 다른 Activation Function에서)... "Gradient Exploding"
: Gradient값이 1이상으로 크다면 똑같은 원리로 Gradient가 무한대로 커지는 현상)
위의 두가지 현상을 방지하기 위함이다.
ReLU는 Nonlinear 함과 동시에 0보다 큰 구간에 대해서는 기울기가 1로 고정되어있기 때문에
Gradient Vanishing, Exploding현상을 어느정도 막아준다.
* 나중엔 Deep Neural Network에서는 쓸모없는 Network를 Gradient Vanishing 과정을 통해 없애기도 한다.
이건 참조만.
단, ReLU도 완전무결한 Activation Function은 아닌데, 그 이유는 'Knock Out'문제가 있기 때문이다.
ReLU에서 한번 기울기가 0으로 떠버린 노드 이후의 Network는 모조리 손실된다. 이를 'Knock Out'이라고 한다.
*단... 이론과 달리 Knock Out은 실제 상황에서는 잘 발생하지 않으며, 오히려 쓸모없는 Network를 없애주는 역할도 하는 것으로 알려져있다..(고 한다.. 자세히는 모르겠고 그냥 ReLU쓰자)
이런 Knock Out 문제를 방지하고자 나온 Activation Function이 바로 Leaky ReLU인데,
임계치보다 작을때 무조건 0을 출력하는 ReLU와 다르게, 0.01을 곱한다.

단, Deep Neural Network에서 실제로는 대부분 Leaky ReLU가 아닌 ReLU를 사용하는데,
Computational Cost측면에서 ReLU가 압도적으로 좋기 때문이다.
◎ Process of G.D in MLP
본격적으로 MLP(Multi Layer Perceptron)의 Back Propagation과정을 들여다보도록 하자.
input, output layer 중간에 tanh Activation Function을 가진 Hidden layer가 하나있을때
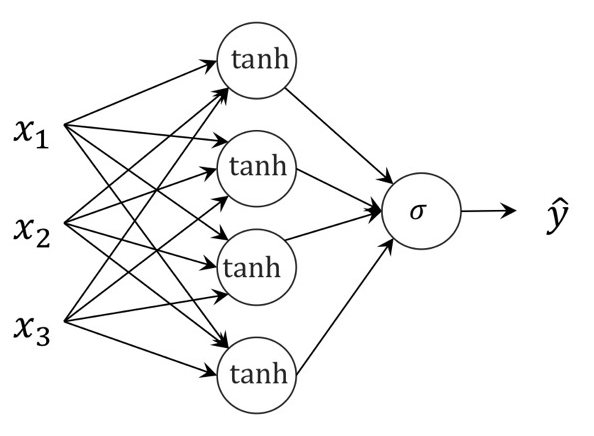
여기서 forward Propagation은 다음과 같은 과정을 거치며

결정해야하는 Parameter는

batchsize = m (Full Batch)의 Back Propagation의 Weight Update는

Loss Function은 Log loss(Cross Entropy)라고 할때,
각 Weight의 Loss에대한 Partial Derivation은 아래와 같다.
포스팅 (1)에서 처럼 Chain Rule을 통해 구해주면 아래와 같은 과정을 거치는데,
(이건 그냥 참조만하고 결과로 바로 건너뛰어도 된다...)
-> 두번째 Layer에서 가중치

b와 같은 방식으로 w에대한 Partial Derivation은

두번째 Layer에서 w,b에 대한 Loss Gradient는
Binary Cross Entropy + Sigmoid Activation 이었던 직전 포스팅 Logistic Regression의 Back Propagation과정과 결과가 똑같다.
-> 첫번째 Layer에서 가중치
이전 방식의 결과를 참조하여, 각 Gradient값을 구해주면...


앞서 두번째 Layer에서는 sigmoid Activation의 Gradient였지만
이번엔 tanh Activation에 대한 Gradient이다. 공식을 천천히 따라가다보면 도출할 수 있다.
-> 결과
...과정은 복잡했지만 결론은 간단하다.
아래와같이 각 Partial Derivative를 정리할 수 있게된다.

이 Derivation값을 Gradient Descent로 각 Weight와 Bias term을 Update해주면 된다.
전체 과정의 이를 pseudo Code화 해주면

'AI > Deep Learning' 카테고리의 다른 글
| Deep Learning (6) _Optimization (0) | 2022.04.23 |
|---|---|
| Deep Learning (5) _ Practical Aspect (0) | 2022.04.22 |
| Deep Learning (4)_DNN (Deep Neural Network) (0) | 2022.04.21 |
| Deep Learning (3)_ Pytorch (0) | 2022.04.20 |
| Deep Learning (1) - Linear Regression, Logistic Regression (0) | 2022.04.20 |




