정리노트
Deep Learning (6) _Optimization 본문
Neural Network는 Cost Function의 최솟값을 Optimal Point로 도출하고,
이를 Analytic Solution이 아닌, 'Iterative Solution'으로 찾는다. -> Gradient Descent
Iterative Solution은 Analytic Solution 처럼 함수 전체에서 Optimal Point를 찾는게 아니라 그때그때 들어온 값에 따라서 Optimal한 지점을 차근차근 찾아나가는 방법이기 때문에, 모든 경우에서 100프로 완벽한 Optimal Point를 찾을 수는 없으며, 심지어는 학습에 실패하기도 한다. (ex. Local Minima, plateau, divergence..etc)
인공지능에서 Iterative Solution은 보통 경사하강법, Gradient Descent기반의 방법들을 이야기하며,
가장 기본적인 형태의 Gradient에서 그 불완전함을 보완하는 여러 기법들이 제시되고 발전되어 왔다.
이렇게 Optimal Point를 찾아나가는 모든 방법들을 통틀어서 '최적화', 즉, 'Optimization'이라고 하고,
(일반적으로는 Maximum, Minimum인 '극값'을 찾는 과정을 Optimization이라 함)
오늘은 이에대한 내용을 다뤄보고자 한다.
Optimizer 의 종류와 특성 (Momentum, RMSProp, Adam) :: 312 개인 메모장 (tistory.com)
Optimizer 의 종류와 특성 (Momentum, RMSProp, Adam)
<!DOCTYPE html> Optimizer Optimizer Optimizer는 딥러닝에서 Network가 빠르고 정확하게 학습하는 것을 목표로 한다. 주로 Gradient Descent Algorithm을 기반으로한 SGD에서 변형된 여러종류의 Optimizer가 사..
onevision.tistory.com
위 블로그에 오늘 포스팅 내용의 거의 대부분이 잘 요약 되어있는데 한번 참고해보면 좋을 듯 하다.
◆목차
◎ Exponentially weighted averages
◎ Stochastic Gradient Descent (SGD) with Momentum
◎ RMSprop
◎ Adam
◎ Using optimization algorithms in PyTorch
◎ Learning rate scheduling (optional)
◎ Exponentially Weighted (Moving) Averages
Exponentially Weighted Averages는 한국어로 지수 가중 평균으로, Exponentially Moving Averages,지수 이동 평균이라고도 한다.
* Optimization이야기 하다가 웬 쌩뚱맞은 지수평균이 나오나 싶은데,
여기서 구한 Exponentially Weighted (Moving) Averages는 GD, SGD, MGD 알고리즘에 더해져서
Gradient의 'Momentum' 개념으로 사용된다.
아래 블로그에 정리가 잘되어있으니 참조
https://wikidocs.net/35847#bias-correction-in-exponentially-weighted-average
4. Optimization Algorithms
> * Remember different optimization methods such as (Stochastic) Gradient Descent, Momentum, RMS ...
wikidocs.net
Exponentially Weighted (Moving) Averages는
데이터가 시간의 흐름에 따라서 어떻게 움직이는지 경향선을 나타내고 싶을때 사용된다.
현재의 데이터값이 과거의 데이터 값의 영향을 받도록한 것이며,
과거의 데이터가 시간의 흐름에 따라 지수적으로 현재 끼치는 영향이 적어지도록 설계한 것이 Exponentially Weighted (Moving) Averages 라 할 수 있다.
식은 아래와같이 간단하다.

Vt 현재의 Moving Everage은 Vt-1 바로 직전 과거데이터의 Moving Everage에 B가중치를 곱한것과 현재 데이터에 1-B가중치를 곱하여 더한 것이다.
아래 수식에서 살펴볼 수 있듯,
B라는 가중치가 계속 곱해져서 시간이 지나면 지날 수록 과거데이터의 영향은 줄어든다.
예를 들어 B = 0.9인경우를 예시로 들면


위 그래프에서 초록선과 빨간선의 차이를 보면 알 수 있듯이,
B가 커지면, 과거의 데이터의 영향이 커지기 때문에 더 Smooth한 그래프가 그려지고, Latency가 커지는 것을 알 수 있다. 반대로 B가 작아지면, 과거의 데이터 영향이 줄어들고 현재의 데이터에 대한 영향이 커지기 때문에, 더 구불구불하고 Latency가 작은 그래프모양을 띄는 것을 알 수 있다.
(B가 0이면 지수이동 평균이 없는거나 마찬가지일거고, 1이라면 Vt= 0인 직선하나가 덩그라니 그려질 것)
○ Bias Correction
RMSprop의 문제점중 하나는,
초반 Initialization을 V0 = 0으로 하기때문에 아직 데이터가 적은 초반부분에는 곡선이 아래로 쳐져있는(Biased) 상태에서 시작하게 된다는 것이다.
아래블로그에 설명이 완벽하게 되어있다.
https://angeloyeo.github.io/2020/09/26/gradient_descent_with_momentum.html#bias-correction
Momentum을 이용한 최적화기법 - ADAM - 공돌이의 수학정리노트
angeloyeo.github.io
Bias Correction은 이런 Biased 상태에 대한 Compensation을 주는 것으로 공식은 아래와같다.

원리는 간단한데,
원래의 이동평균선 공식의 결과에 1-B^t 만큼을 나눠주면 된다.
(매 t마다 나눠지게 되면서 초기값 bias에 대한 Compensation이 되는구조)
이를 그림으로 표현해서 비교하면

* 1-B^t만큼 나눈게 왜 Compensation인가? 에대해서는 자세히 유도하진 않겠다
"초기 1- B, B Term에 의해작아진 값들에대한 Normalization" 정도로 이해해두면 될듯 하다.
◎ Stochastic Gradient Descent (SGD) with Momentum
앞선 포스팅 https://roboharco12.tistory.com/25?category=1038783에서
Deep Learning (4)_DNN (Deep Neural Network)
지금까지 포스팅에서 다룬 내용은 뉴런 노드 하나(Linear Regression + Activation Function)부터 시작해서 Shallow Neural network를 Gradient Descent 과정을 거쳐서 직접구현을 해봤고, pytorch Framework를 보..
roboharco12.tistory.com
Gradient Descent (Full Batch)와 Mini-batch Gradient Descent (mini-Batch)와 Stochastic Gradient Descent (1 Batchsize)
를 비교했었다.
○ intuition of SGD with Momentum
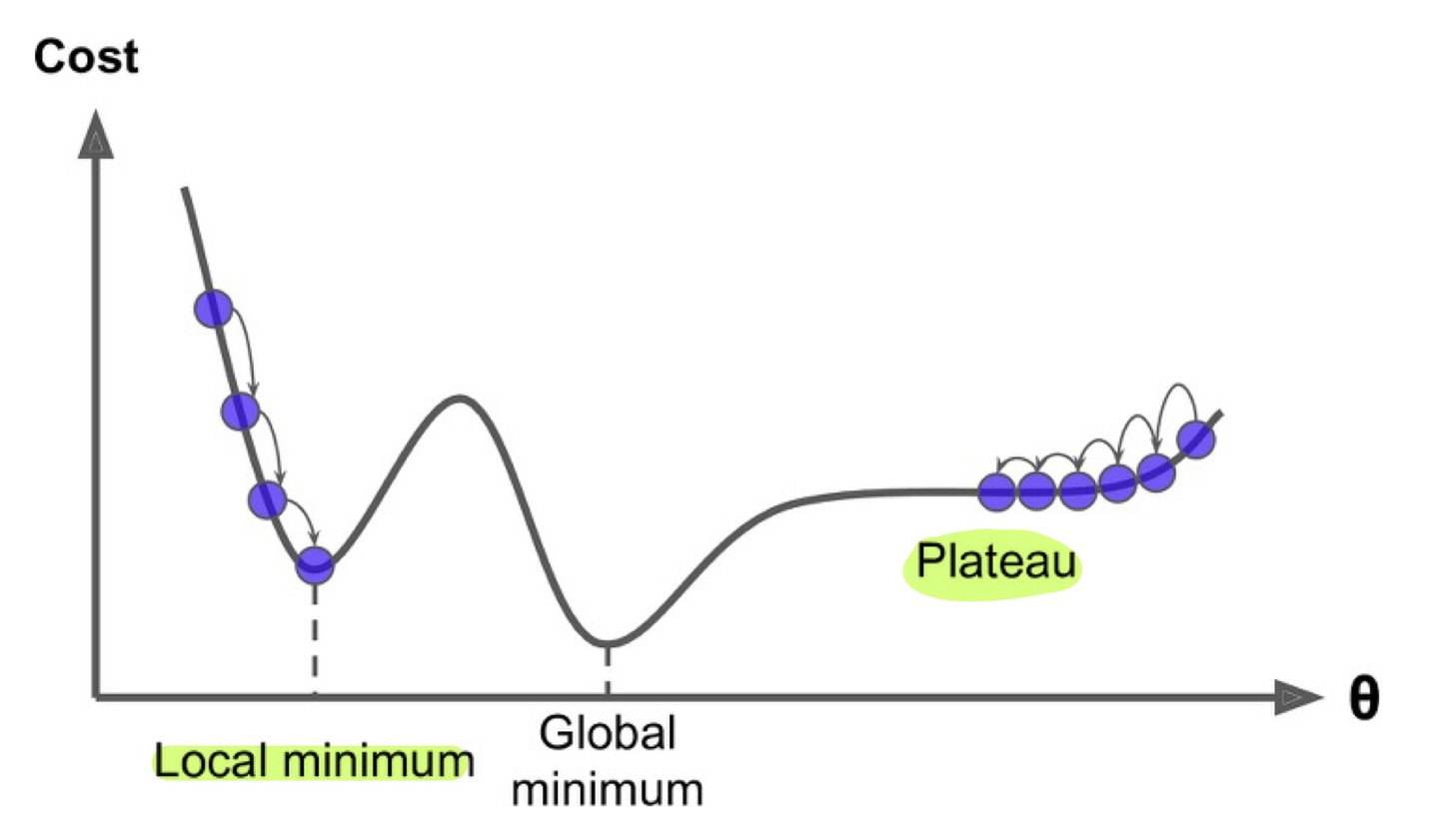
Gradient Descent에서 가장 피하려고 하는 상황은, Gradient값이 0임에도 Global Minimum에 수렴하는 것이 아닌 엉뚱한 지점에 수렴하는 상황이다.
이 피해야하는 엉뚱한 지점에는 크게 두가지가 있는데,
1, Local Minimum
2, Plateau
두 지점 모두 Gradient가 0에 수렴하다보니,
Classic한 GD에서는 Weight의 움직임이 거의 없어서 학습이 잘 이뤄지지 않는다.
여기서, 앞선 섹션에서 다뤘던 Exponentially Weighted (Moving) Averages를 Gradient의 'Momentum'처럼 사용하면
이 두 지점을 더 잘 탈출할 수 있는데,
확실한 지점에 대해서는 Stochastic Gradient Descent보다 안정적이고 빠르게 Global Mimum을 찾아갈 수 있다.
이에 대한 그림과 수식은 아래와 같다

Gradient Descent식에 이를 표현해주면,

Gradient 값이었던 dL/dw, dL/db대신,
각 Gradient의 추세, 즉, Momentum을 대신 넣어준다.
이렇게 함으로서 이전 Gradient의 거동에 대한 가중치가 더해져서 Gradient가 이동하게 되고,
더 안정적이고 정확한 수렴이 가능해진다.
◎ Adagrad
두번째로 다뤄볼 Optimization기법은 Adagrad이다
*수업땐 따로 다루진 않았지만 RMSprop를 보기전에 Adagrad를 먼저 정리해둬야 할 것같아서 첨부해둔다.
https://deep-learning-study.tistory.com/158
[딥러닝] 매개변수 갱신 - AdaGrad 기법
사이토고키의 <밑바닥부터 시작하는 딥러닝>을 공부하고 정리하였습니다. AdaGrad 신경망 학습에서는 학습률 값이 중요합니다. 이 값이 너무 작으면 학습 시간이 너무 길어지고, 반대로 너무
deep-learning-study.tistory.com
Adagrad는 Gradient Descent기법에서 Learning Rate, 즉, Step size를 점점 작게 조절하며 Optimal Point를 찾아나가는 알고리즘으로,
전체 파라미터에 대해서 일괄적으로 Learning Rate를 조절하던 기존 알고리즘 과 달리,
파라미터 각각에 아래와 같은 공식을 적용하여 Learning Rate를 작게 만들어준다.

공식을 살펴보면, learning Rate에 루트h로 나누어 조절하고 있음을 알 수 있는데, h를 보면 이전 h값에 parameter에대한 Loss의 Partial Derivation의 제곱값을 계속해서 더하는 것으로 나와있다.
위 공식을 해석해보면
파라미터 변화가 작은데 Loss변화가 크다 -> Learning Rate를 더 작게 -> Optimal한 지점에 가까우니까 덜움직이게!
파라미터 변화가 큰데 Loss변화가 작다 -> Learning Rate를 덜 작게 -> Optimal한 지점에서 머니까 더움직이게!
* Adagrad의 단점은 h에 Loss 기울기 제곱값을 계속 더하기만 하다보니 h의 값은 항상 양의 값으로 커질 수 밖에 없고,
iteration이 커지면 아직 수렴했는지 여부와 별개로 Learning rate가 0에 수렴하여 paramete가 더는 갱신되지 않는다는 점이다.
이 단점을 보완한 것이
위에서 다룬 '이동평균'개념을 도입하여 Learning rate를 조절하는 RMSprop라는 알고리즘이다.
◎ RMSprop
RMS Prop의 공식은 아래와 같다.

위에서 이동평균에 대한 내용과, Adagrad에 대한 내용을 잘 숙지했다면
어렵지않게 이해할 수 있을 것이다.
○ RMSprop의 Geometric한 해석방법
RMSprop는 Adagrad에서 Stepsize를 줄이는 방식을 Exponentially Moving Everage를 이용하여 Learning rate에 대한 Normalization 해준 것이라고 하였다.
이를 관점을 조금 바꿔서 접근하면...
Learning rate 관점이 아닌 W,b에대한 관점으로 바꿀 수 있는데 위의 식을 아래와 같이 바라볼 수 있는것이다.

이를 그림으로 표현하면....
W,b가 움직이는 차원에대해 크기를 Isotropic하게 맞춰주는 일종의 Normalization과 같은 역할로 생각할 수 있다.

* RMS에서도 지수 이동 평균이 이용됐는데, 이것도 모멘텀 아니야?
->.. 공부하면서 제일 헷갈렸던 부분인데,
SGD with Momentum에서의 Momentum은 Gradient 방향 자체에 대한 Momentum이고 (그래서 분자값)
RMSProp에서 쓰이는 Momentum은 그 움직이는 대상이 Gradient가 아닌
Learning rate, 혹은 Weight Space(w,b)의 Normalization에대한 Momentum 이라는점에서 다르다고 볼 수 있다.
그래서 조금은 부차적인 부분에서의 Momentum이라고 보기 때문에 Momentum계열로 안치는 듯 하다
* 앞서https://roboharco12.tistory.com/26 포스팅에서 Normalization에 대한 내용을 다뤘었다.
Deep Learning (5) _ Practical Aspect
이번 포스팅에서는 딥러닝 네트워크를 구축하면서 염두해두어야할 내용들에 관한 내용이다. Deep Learning에 국한되어 적용되는 개념들은 아니고, Machine Learning Algorithm에서도 전반적으로 알고있어
roboharco12.tistory.com
위 포스팅 내용과 RMSprop는 Normalization의 intuition은 같지만, 그 대상이 다르다.
위 링크에서 이야기하는 Normalization은 Feature Size에 대한 것들이라면,
여기서 이야기하는 RMSprop의 Normalization은 Model Parameter Size에 대한 Normalization을 말한다.
◎ Adam
지금까지 MGD, SGD의 단점을 보완하는 알고리즘을 크게
StepSize 관점에서 보완한 Adagrad, RMSprop,
Step방향 관점에서 보완한 Momentum
세가지를 다뤄보았는데,
Adam은 RMSProp와 Momentum을 융합한 방법으로,
-> Momentum은
momentum 계수 V에 Learningrate를 곱한 것이고,
-> RMSProp는
(Learning rate)/루트(Parameter 이동평균)에 Gradient를 곱한것 으로, Parameter를 Update해 나가는 방식인데,
이 두가지 장점을 합치면 아래와 같은 Adam 알고리즘이 나온다
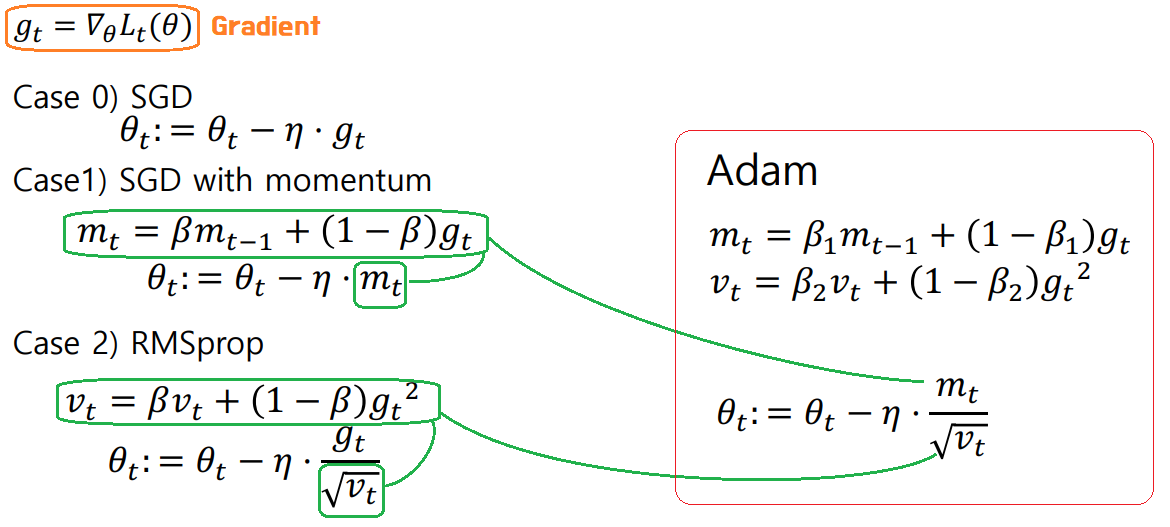
-> Adam Optimizer는
1차 모멘텀계수와 2차 모멘텀계수를 설정해줘야하므로,
Momentum과 RMSProp이 Learning rate, 모멘텀계수 2개의 Hyperparameter만 설정해주면 됐던 것과 달리,
3개의 Hyperparameter를 설정해 주어야 한다.
+ 보통 1차모멘텀계수 B1 = 0.9, 2차 모멘텀 계수 B2 =0.999로 기본설정 값을 놓으면 잘 동작한다고 한다.
Adam Optimizer Pseudo Code는 아래와 같다.

위에서는 mt, vt에대한 Bias Correction된 값이 들어가있다.
* 이번 포스팅에서 다루는 모든 Optimizer가 정리되었다 !
큰 흐름을 그림으로 그리면 아래와 같다

이전 DeepLearning(4) DNN포스팅에서
Minibatch Gradient Descent와 Stochastic Gradient Descent의 기본적인 알고리즘에 대해 다뤘고,
이번 포스팅에서 지금까지 Learning rate와 Momentum 조절을 통해 MGD,SGD의 단점을 보완하는 알고리즘인
Momentum, Adagrad, RMSprop에 대해서 다룬 후,
최종적으로 RMSprop와 Momentum Optimizer가 합쳐진 Adam Optimizer에대해 다루어보았다.
◎ Using optimization algorithms in PyTorch
개념은 끝났고, Pytorch에서 이를 어떻게 구현하는지 간단히 정리해보겠다.
앞선 포스팅에서도 다뤘지만, 모델을 학습시키기 앞서서 아래 그림처럼
Optimizer와 Costfunction에 대한 정의를 해주어야 학습을 진행할 수 있다.

Costfunction에 대해서는https://roboharco12.tistory.com/22
포스팅에서 첫부분에 다루었다.
Optimizer는 이번포스팅에서 다루는 것으로,
아래에서 torch에서 제공하는 모든 Optimizer를 확인할 수 있다.
https://pytorch.org/docs/stable/optim.html
torch.optim — PyTorch 1.11.0 documentation
torch.optim torch.optim is a package implementing various optimization algorithms. Most commonly used methods are already supported, and the interface is general enough, so that more sophisticated ones can be also easily integrated in the future. How to us
pytorch.org
이번 포스팅에서 다뤘던 Optimizer를 간단히 살펴보면

◎ Learning rate scheduling (optional)
Learning rate에대해서 알고리즘 적으로 조절해주는 Adagrad, RMSProp같은 방식이 아니라,
pytorch에서 제공하는 스케쥴러를 이용하여 외부에서 이를 조절해 줄 수도 있다.

이런식으로 Optimizer뒤에 Scheduler를 설정해준 후, training상에서

을 Iteration 시켜주면 된다. (...그냥 Scheduler하나 추가한게 전부다)
아래 두 블로그에서 이내용이 잘 정리되어있으니 참조
[PyTorch] PyTorch가 제공하는 Learning rate scheduler 정리 (tistory.com)
[PyTorch] PyTorch가 제공하는 Learning rate scheduler 정리
(여기 내용을 많이 참고하여 작성하였습니다.) (** learning rate와 lr이라는 용어를 혼용해서 작성하였습니다.) learning rate는 gradient의 보폭을 말한다. learning rate는 성능에 꽤나 영향을 주는 요소(lear..
sanghyu.tistory.com
Guide to Pytorch Learning Rate Scheduling | Kaggle
Guide to Pytorch Learning Rate Scheduling
Explore and run machine learning code with Kaggle Notebooks | Using data from No attached data sources
www.kaggle.com
이 포스팅에서
몇가지만 간단히 소개해보면
- Exponential LR

Learning rate가 gamma의 지수배로 감소하는 알고리즘
- MultiStepLR

Mile Stones로 정해둔 Epoch에서 Learning rate를 gamma배 만큼 감소시키는 알고리즘
- Others...

'AI > Deep Learning' 카테고리의 다른 글
| Deep Learning (8)_Tensorboard & Tuning Parameter (0) | 2022.05.21 |
|---|---|
| Deep Learning (7) _Batch Normalization (0) | 2022.05.21 |
| Deep Learning (5) _ Practical Aspect (0) | 2022.04.22 |
| Deep Learning (4)_DNN (Deep Neural Network) (0) | 2022.04.21 |
| Deep Learning (3)_ Pytorch (0) | 2022.04.20 |




