정리노트
Deep Learning (1) - Linear Regression, Logistic Regression 본문
Deep Learning (1) - Linear Regression, Logistic Regression
Krex_Kim 2022. 4. 20. 02:35Neural Network의 각 뉴런의 구조는
Linear Regression의 output이 Activation 함수를 통과하는 구조 로 이루어져 있다.
그리고 Logistic Regression은 Linear Regression의 output이 Sigmoid Function 함수를 통과하여
그 값(확률)이
0.5 이상일때를(W*X+b = 0.. Decision Boundary) Threshold로 Classification해준 것이다.
Neural Network를 구성하고 있는 이 모델들 하나하나를 'Perceptron', 또는 'Neuron'라고 부를 수 있는데,
이때 가장 'Optimal'한 Weight(가중치) 'W'와 Bias Term 'b'를 Iterative Solution으로 찾아주는 방식(Gradient를 활용하는)을 이용하여 Neural Network를 학습시킨다.
이번 포스팅은
바로 이런 Neural Network 학습과정을 이해하는데 첫걸음이 되는
"Linear Regression", "Logistic Regression"에 대한 내용을 쭉 정리해볼 것이다.
◆ 목차
◎ Linear Regression
◎ Optimization
◎ Logistic Regression
◎ Gradient Descent (Back Propagation)
◎ Linear Regression VS Logistic Regression
◎ Linear Regression
Linear Regression을 한마디로 정리하면
"input Variables(Features) 와 Output Value가 Linear한 관계임을 가정하고, 이때 가장 Optimal한 Linear subspace를 찾아내는 알고리즘" 이라고 할 수 있다.



아래 좋은 예시가있어서 첨부해두었다. 야구에서 Run Value(득점가치)를 예측해내는 모델로,

x1, x2.. 각 Instance는 안타, 볼넷, 아웃, 삼진, 홈런, 도루 총 6개의 Feature를 가지고 있고, 이에대해서 Runvalue, 점수예측을 한다고 했을때,
Linear Regression은
무수히 많은 instance 개수로 Linear 모델 y를 학습시킨후 제일 에러가 적은 Weight값을 뽑아내는 것이다.
이 Linear Regression모델로 해당선수의 행동(안타,아웃,삼진,홈런 등의)이 경기에서 얼마만큼의 Run Value(득점가치)를 가졌는지 예측할 수 있게된다.
◎ Optimization
Optimization은, 모델은 '최적화', 즉, Optimal Solution을 찾겠다는 의미로,
인공지능에서는 보통 모델의 'Error'값에 대한 정의를 'Cost Function'이라는 함수형태로 정의하고 이를 최소화 하는 W,b를 구한다.
Cost Function은 Loss, MSE, MAE, Cross Entropy Loss 등등 여러가지 종류가 존재한다.
어떤 Cost Function을 써야하는지는 상황에 따라 다르기때문에 여러가지 Reference를 참조하며 모델을 구성해주면 된다.
* 아래블로그 참조
https://leechanhyuk.github.io/machine_learning/Cost_function/
[Concept summary] Cost(Loss) function의 종류 및 특징
Cost(Loss) function
leechanhyuk.github.io
[머신러닝] 손실함수의 종류
손실 함수(loss function)란?머신러닝 혹은 딥러닝 모델의 출력값과 사용자가 원하는 출력값의 오차를 의미손실함수는 정답(y)와 예측(^y)를 입력으로 받아 실숫값 점수를 만드는데, 이 점수가 높을
velog.io
초기 인공지능에서는 Linear Algebra, Convex Optimization을 통한 Analytic Solution에 대한 접근이 있었지만,
Cost Function의 복잡도가 애초에 말도안되기 때문에 일찍이 접었고,
현재는 모두 Iterative Solution을 쓴다. (Discriminative Model)
이중 가장 대표적인 Solution이 바로 그 이름도 유명한 Gradient Descent이다
○ Gradient Descent
Gradient Descent는 Optimization을 다루는 대부분의 분야에서 사용되는 방식이다.
원리는 간단한데, 1차 Derivative Operation인 Gradient를 이용하여 해당 부분이 'Convex' 하면서
기울기가 0에 가까운 지점을 'Iterative' 방식으로 찾아주는 것이다.

○ (참고) 그외 Optimizer들
딥러닝은 적게는 수천, 많게는 수만개의 Perceptron의 GD(Gradient Descent)을 Backpropagation을 통해 계산해주기 때문에, Optimizer를 깡으로 Gradient Descent로 사용하진 않고, 보통 아래 그림처럼 상황에 맞게 선택해서 사용한다.

이에대해서는 Optimization 포스팅에서 따로 자세히 다루도록 하겠다
◎ Logistic Regression
Linear Regression을 제대로 이해했다면, Logistic Regression은 간단하다.
Linear Regression의 Output Value를 다시 Sigmoid Function에 넣어주면 된다.
Linear Regression Model은 아래와같았다.

Sigmoid Function은

즉, Logistic Regression Model은 다음과 같다.

Sigmoid function의 input값이 0일때, 그 값은 1/2 = 0.5가며,
이때를 기준으로 더 크면 1, 작으면 0으로 Classification해주는 방식으로 작동된다.
그리고 input값이 0일때, 즉, W*x+b = 0일때가 이 모델에서의 Decision Boundary가 된다.
◎ Gradient Descent (Back Propagation)

○ Logistic Regression에서의 Gradient Descent
앞선 Optimization 섹션에서, Linear Regression, Logistic Regression에서 Optimization은 Gradient값을 이용해서 Iterative하게 구해준다고 이야기했다.
이 과정에 대해서 조금 자세히 들여다보자.

Logistic Regression모델을 쭉 펼쳐보면 위의 그림과 같다.
Loss Function을 Binary Cross Entropy라고 설정하면,


여기서 우리가 알아야 하는건, Weight, W={w1,w2}와 Bias Term, b이므로,
우리가 알아야하는 Gradient값은 dL/dw, dL/db이다.
Cost Function을 Cross Entropy로 설정해주고
dL/dw, dL/db를 구해주면
아래와같다.

Chain Rule을 적용해주면 아래와같다.

이를 한번 더 정리하면,

b는 x3 = 1이라고 놓고 w와 같은 back Propagation과정을 거친다면
w1,w2,b 3개의 파라미터에 대해 아래와 같은 결론을 가질 수 있다.
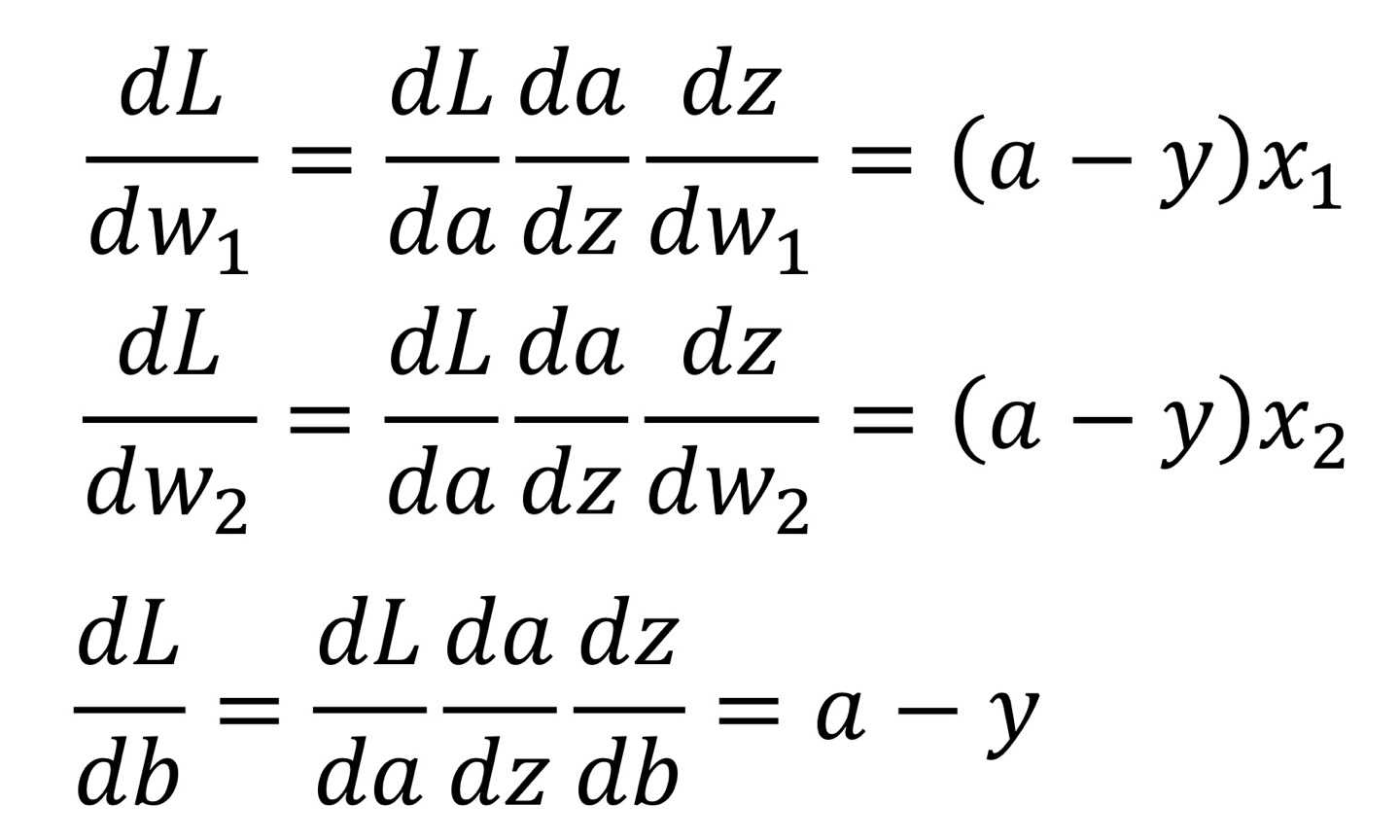
이를

해줌으로써 w1,w2,b값을 Update해준다.
그리고 업데이트 과정을 계속 반복해준다.
예시는 Linear Regression에 Activation을 통과한 노드 하나 뿐이었지만,
우리가 다루게 될 Neural Netwok에서는 이것이 층구조로 여러개 연결되어 수십, 수백, 많게는 수만개의 W와 b를 Update해주게 된다.
Output Value 'Prediction' a와 'Label' 'y'간의 Loss로부터 각 노드간 연결 Weight값을 뒤로가며 하나씩 도출해냄으로,
이를 'Back Propagation'이라고 부른다.
위의 예시에서는 학습 한번당 한개의 샘플, 즉 Batch size가 1이었는데,
만약 Batch size가 m개면, m개 샘플의 loss의 평균 값을 가지고 Back Propagation해주면 된다.
즉,
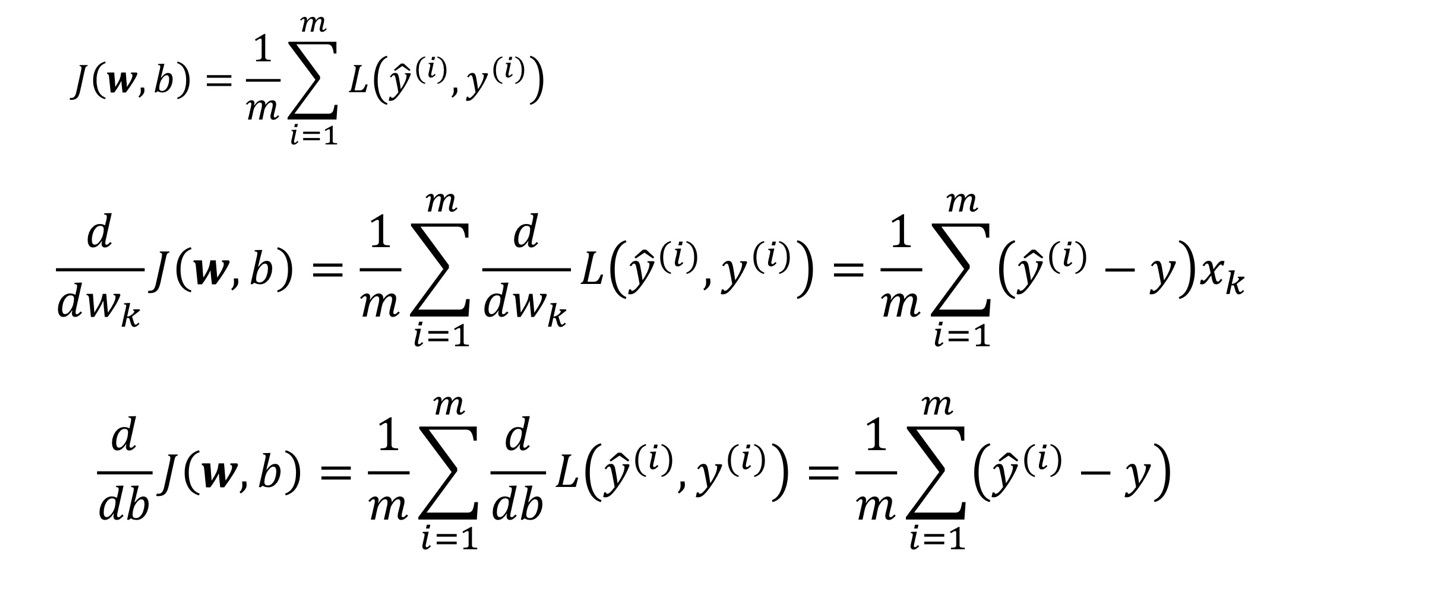
Batch size = m 의 Weight Update pseudo Code는 아래와 같다

○ Linear Regression에서의 Gradient Descent
Logistic Regression은 Discrete Class를 예측하기위한 모델이라면,
Linear Regression은 Continous Value를 예측하기위해 만들어지 모델이다.
Logistic Regression과 Loss Function을 MSE(Mean Square Error)로 설정해 주었다는 점만빼면 모든 과정이 동일하다.
MSE(L2 Norm)의 Gradient값은 아래와 같고,

만약 Batch Size가 m개라고 하면,
m개에대한 평균 Loss를 propagation해주면 되는데, 아래 예시와 같다.
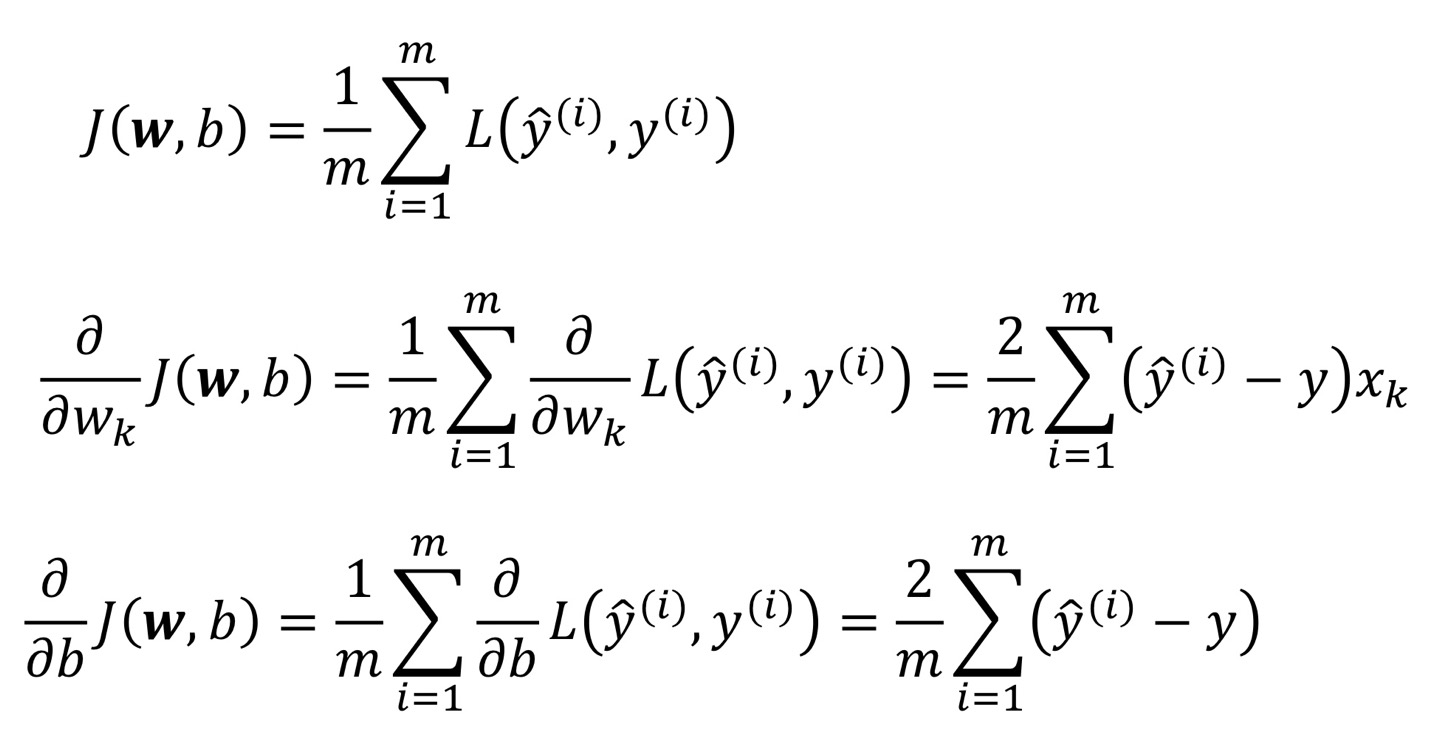
정리하면

w, b와 그에 대한 Loss 값의 Gradient값을 도출 했으므로,
아래의 Pseudo code에 그대로 적용해주면 된다.

◎ Linear Regression VS Logistic Regression
모델의 작동에서 차이점은 Sigmoid를 통과 했냐 안했냐의 차이정도지만,
두 모델은 목적자체가 다른데,
Linear Regression은 Continous한 Value값을 예측하지만(Regression)
Logistic Regression은 Discrete한 Class를 Classify한다.(Classification)
아래 그림이 이를 잘 설명해준다.

위 그림을 보면 Label Data자체가 Linear Regression의 경우 Continous하고,
Logistic Regression의 경우 Discrete한 것을 확인할 수 있다.

*위 표는 Linear Regression과 Logistic Regression를 비교해놓은 표로,
한가지 유념해 두어야 할 것은 (왜인지는 모르겠으나) Logistic Regression에서는 주로 BCE를 쓰고,
Linear Regression에서는 주로 MSE를 쓴다는 것이다
그리고 이때 각 Cost Function의 Gradient값은

비슷하다.
'AI > Deep Learning' 카테고리의 다른 글
| Deep Learning (6) _Optimization (0) | 2022.04.23 |
|---|---|
| Deep Learning (5) _ Practical Aspect (0) | 2022.04.22 |
| Deep Learning (4)_DNN (Deep Neural Network) (0) | 2022.04.21 |
| Deep Learning (3)_ Pytorch (0) | 2022.04.20 |
| Deep Learning (2)_ Shallow Neural network (0) | 2022.04.20 |




