정리노트
Frequency Response Method - polar plot 본문
이번 포스팅에서 다뤄볼 내용은, 바로 주파수응답을 표현하는 방법에대한 내용이며,
그중 Polar plot에대해 다뤄보고자 한다.
우리는 시간, Time domain안에서 살고있기때문에 시간이라는 물리량 기반으로한 해석법에는 능숙하다.
하지만, 시스템이 어떻게 거동하는지 살펴볼 상황이 됐을때,
시간기반의 해석방법보다 주파수 기반의 해석방법이 더 유용할때가 많다.
이런 주파수기반의 해석법을 적절히 표현하기위해 여러가지 Notation들이 개발되었으며,
그중 대표적인 예시는 Bode Plot(다음포스팅에서 다룰), 그리고 Polar Plot이다
목차는 다음과 같다.
◆목차
◎ Frequency Response
◎ Intro
◎ Polar Plot
◎ Frequency Response
먼저 '주파수 응답' 이라는 단어의 정의부터 내리고 시작해보자.
주파수에대한 어느정도의 지식이 있다면, System Response에는 크게 Transient Response(과도응답)와 Steady state Response(정상상태응답(?)) 두가지가 있다는 점은 알것이다.
'주파수 응답', Frequency Response이란, sinusoidal input에대해서 Steady State Response, 시간이 어느정도 지난후의 시스템의 Response로 정의내려진다.
그리고 이때 짚고가야할 특성하나가 있는데,
System이 Linear할때(보통 그렇게 해석을 하니까), Sinusoidal input이 들어오면 그 Output역시 Sinusoidal output으로 출력된다는 점이다. (이에대한 증명은 다루지 않도록 하겠다)
(물론 input, output의 magnitude와 phase는 당연히 다르다)
그렇기때문에 다음과같이 sinusoidal input이 가해진 Linear System이 있다고 했을때


Steady State Output은 아래와같이 sinusoidal하다.

그리고 이때 Output의 Magnitude와 Angle Phase는 주파수 domain의 variable, w로 표현할 수 있다.

즉, 우리는 w를 통해 System의 Frequency Response, 즉, Steady State Response에대해 완벽히 정의내릴 수 있게된다.

◎ intro
시스템의 Response를 Graphical 하게 해석하는 방법들에대해 본격적으로 다뤄보기전에
알아야할 것들에대한 내용이 있다.
(이해하기가 다소 난해하거나, 복잡할 수 있는 내용들이라, 결론만 알고 넘어가도 좋다.)
우리가 결국 해석하고자 하는 최종식은 아래와같다.

그리고 input은

Transfer Function은
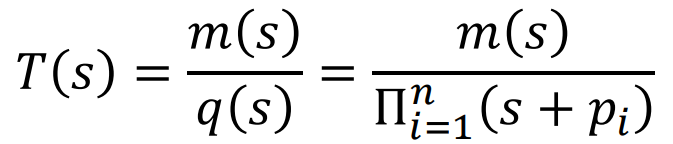
여기서 두가지 가정이 들어간다.
첫째로 Repeated Pole이 없다고 가정하면
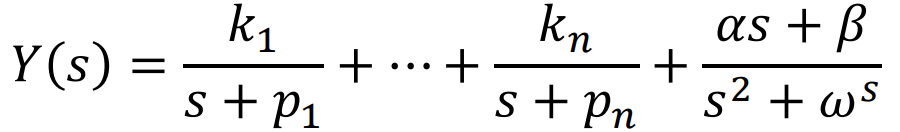
라고 쓸 수 있다. 기존 TF의 n개의 pole과, sinusoidal input이 만들어낸 Term 까지 고려하면 합리적인 표현이다.
두번째로 Pole이 Positive Real part라고 하면
(모든 Pole이 LHP에 존재하게되므로, '시스템이 Stable하다고 가정하면,'과 동의어가 된다.)
inverse Laplace Transform을 하여 본 Steady State Response 결과는, 앞서 n개의 positive pole Term은
모두 0으로 수렴하게되고,
최종적으로 아래와 같아진다.

즉, Steady State Response는

라고 쓸 수 있으며, Angle Phase는

이 된다.(솔직히 왜인지는 모르겠고 일단 응그렇구나 했다..)
위 과정의 결론은, 결국 sinudoidal output은 Transfer Function을 보아야 결정할 수 있게된다는 것이다.
Magnitude에서 input의 magnitude를 A라고 할때
output의 magnitude는 TF의 Magnituce와 input의 Magnitude(상수)를 곱한값같으며
Phase는 TF에 s= jw 를 넣었을때의 Phase와 같다.
이 결론을 정리하면 아래와 같다.

그리고

결론:
Linear System에 Sinusoidal Input이 들어갔을때, sinusoidal output은
T(jw)를 해석함으로서 해석가능하다... magnitude는 T(jw)의 magnitude에 sinusoidal input의 크기를 곱한것과 같으며,
Phase는 그냥 T(jw)의 Phase이다.
-> input은 magnitude에대한 정보만 제공할 뿐, 해석할때 쓰이지 않는다는 말이다.
아래의 해석법은 Unit Sinusoidal input이 가해진 상황에서의 해석이다.
Example 1)

위와같은 TF가 주어져있을때,

G(jw)의 Real part와 imaginary part를 자세히 살펴보자.
이를 Graphical하게 표현하면

Example 2)

라고하자. (여기서 K는 input의 Magnitude처럼 해석할 수 있을 것이다.)
magnitude와 phase는

이를 graphical하게 표현하면

지금까지 polar plot의 대략적인 개념을 다뤄보았는데,
사실 Bode Plot에 비해 너무 직관적이지 못한탓에 잘 안쓰이는 것으로 알아서
얼추정도의 개념만 정리하고 넘어갔다..
다음 포스팅에서는
제어에서 중요하게 다뤄지는 Bode Plot를 다뤄보도록 하겠다.
'Control > 자동제어' 카테고리의 다른 글
| The Root Locus(2) (0) | 2021.12.03 |
|---|---|
| The Root Locus(1) (0) | 2021.12.03 |
| The Stability of Linear Feedback System (0) | 2021.11.23 |
| The Performance of Feedback Control Systems (2) (0) | 2021.11.13 |
| The Performance of Feedback Control Systems (1) (0) | 2021.11.12 |




