정리노트
The Stability of Linear Feedback System 본문
이번 포스팅에서 다뤄볼 주제는 바로 시스템의 안정성, 'Stability'이다.
◆목차
◎ Stability
◎ Routh-Hurwitz Criterion
◎ Routh-Hurwitz Criterion: Special cases ★
◎ Relative Stability
◎ Stability in state space
◎ Stability
앞선 포스팅에서 언급했듯,
시스템이 안정하다, Stable하다는 것은, Bounded Input에 대해서 Bounded Output, Bounded Response를
토해내는 시스템을 의미한다.
아래 그림은 이런 Stability를 설명하는 좋은 그림이다.


S-Plane해석에서. Pole의 위치가 왼쪽에 위치하면 외부 Disturbance에 의한 반응이 점차 계속 감소하며,
오른쪽에 위치한경우, 오히려 신호가 증폭된다.
그리고 jw imaginary축에 위치한경우(real part가 0인경우) 신호는 중립을 유지,즉 'Marginally Stable'하거나,
또는 Envelope가 커지며 오히려 Divergence, Unstable해지기도 한다.
○Forced Response, Natural Response
... 앞선장에서 언급했던 내용을 한번더 정리해보자
Total Response는 Forced Response, 시간이 흘렀을때 변하지않고 머물러있는 Response,
Natural Response, 시간이 흐르면서 사라지는 Response로 나눌 수 있다.

이에따른 반응을 정리해보면 아래 3가지로 정리.

아래 예시를 통해 가볍게 정리해보면

여기에 impulse input이 들어갔을때의 Response는 아래의 식과 같다.

여기서는 impulse input이므로, Forced Response는 없으며,
첫번째, 두번째의 Term모두 시간이지나면 0으로 수렴하는 Natural Response가 된다.
○Definition of Stability
어떤 시스템이 'Stabe하다'고 했을때 어떤 판단기준을 가지고 있어야하며,
어떤 해석을 해야하는지에대해서 한번 쭈우우욱 정리해보려고 한다.
우선, 앞에도 계속 정리하고 넘어갔던, Stable, Unstable에 대한 정의이다.


Stable하다는 것은, BIBO(Bounded Input, Bounded Output)한 특성을 띄는 시스템을 말하며,
Unstable하다는 것은, BIBO특성을 만족하지 못하는 시스템(Bounded Input Unbounded Output),
Marginally Stable하다는 것은, 몇몇 input에는 Stable하지만, Unstable하게 반응하는 input이 존재할 때를 의미한다.
*여기서 한가지 짚고 넘어갈 부분은, Stability는 "모든" Bounded input을 대상으로 한다는 것이다.
Impulse에서 Stable하고, Step input에서 Marginally Stable, 그 이상의 input에 대해서는 Unstable하다면
그 시스템은 Unstable한 시스템이라고 할 수 있다.
시스템의 Stability를 판단하는 방법에 여러가지가 있는데,
우선 가장먼저 알고 있어야하는 개념은 바로 S-Plane상에서의 해석법이다.
S-Plane에서 Pole의 위치의 영역을 크게 LHP, RHP 그리고 On the imaginary Axis 3가지로 나눌 수 있으며,
각각의 영역에 대해 아래와 같이 해석이 가능하다

Pole이 Imaginary축에 놓여있으면서 Unstable한 예시를 가볍게 살펴보자.
(보고 응 그렇구나 하면된다)
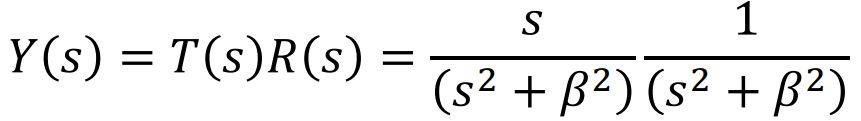
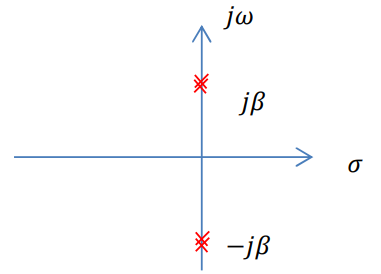
이 예시에서 조금 특이한점은 S Domain 에서 Derivative를 이용한다는 점이다.
아래 식을 살펴보자.
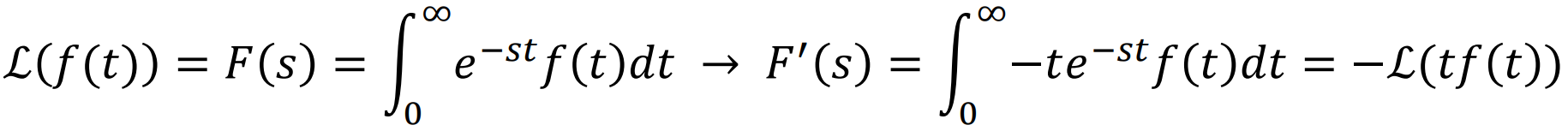
이를 이용하면
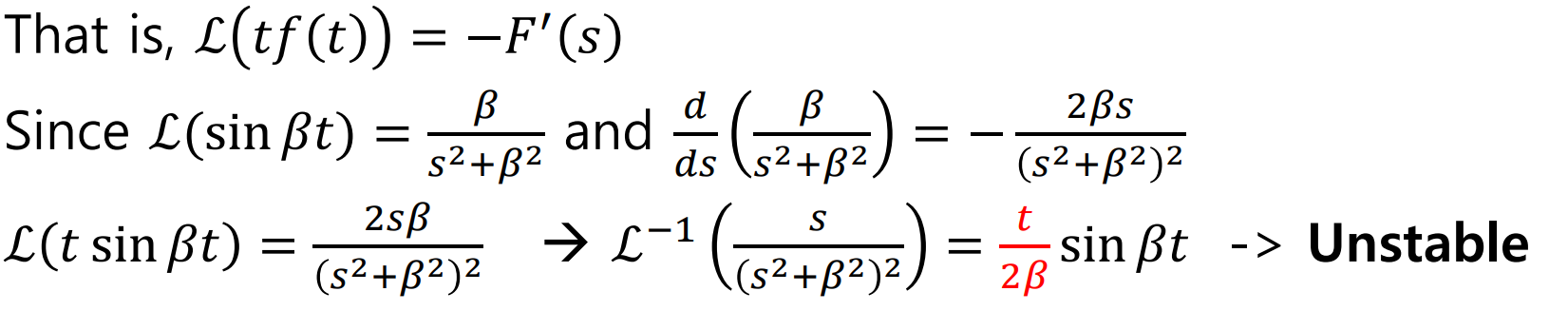
즉, 위의 System Output signal은 Unstable하다고 할 수 있다.
◎ Routh-Hurwitz Criterion
Routh-Huriwitz Criterion은
Closed Loop System의 Pole이 LHP에있는지, RHP에있는지 혹은 imaginary 축 위에 존재하는지
판단하게해주는 하나의 도구로, Pole의 실제 위치까진 알 수는 없지만
어느 영역에 위차하였는지 판단할 수 있게함으로서 시스템이 안정한 상태인지 구분지을 수 있게된다.
이에대한 자세한 내용은 다음과 같다.
만일 Closed Loop System의 분모가 0이라면,
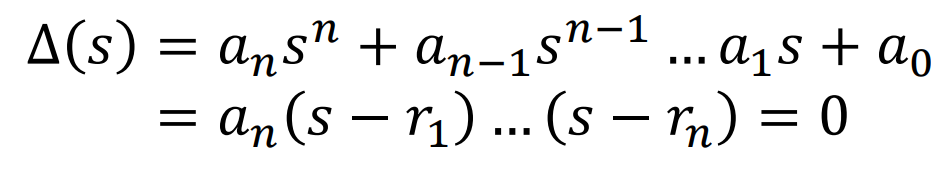
에서,
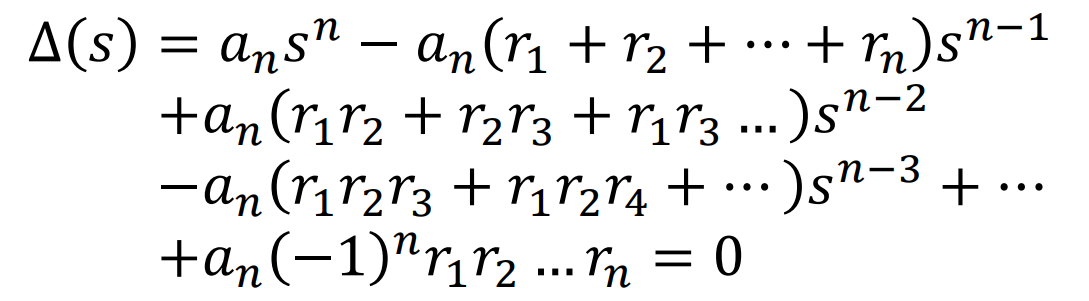
로 정리된다.
여기서, 모든 Pole의 위치가 LHS라면,
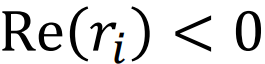
위와같은 관계가 성립된다.
그리고 이것은 아래의 내용과 필요충분 조건이된다.

즉, 위의 내용이 Routh Hurwitz Criterion의 조건이 되는데,
일단 여기서는 응 그렇구나 정도 해두고 결론만 알아보도록하자
○ Routh Hurwitz Criterion
아래와 같은 Closed Loop System의 Transfer Function이 있다고 하자.
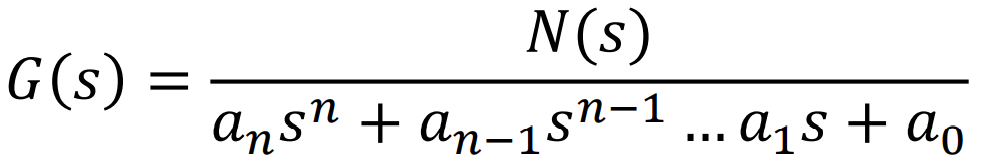
여기서, 우선 아래와같이 Table을 만들어 보자

여기서, S^(n)번째 열과 S^(n-1)번째 열의 수를 이용해 S^(n-2)번째 열을 써주면
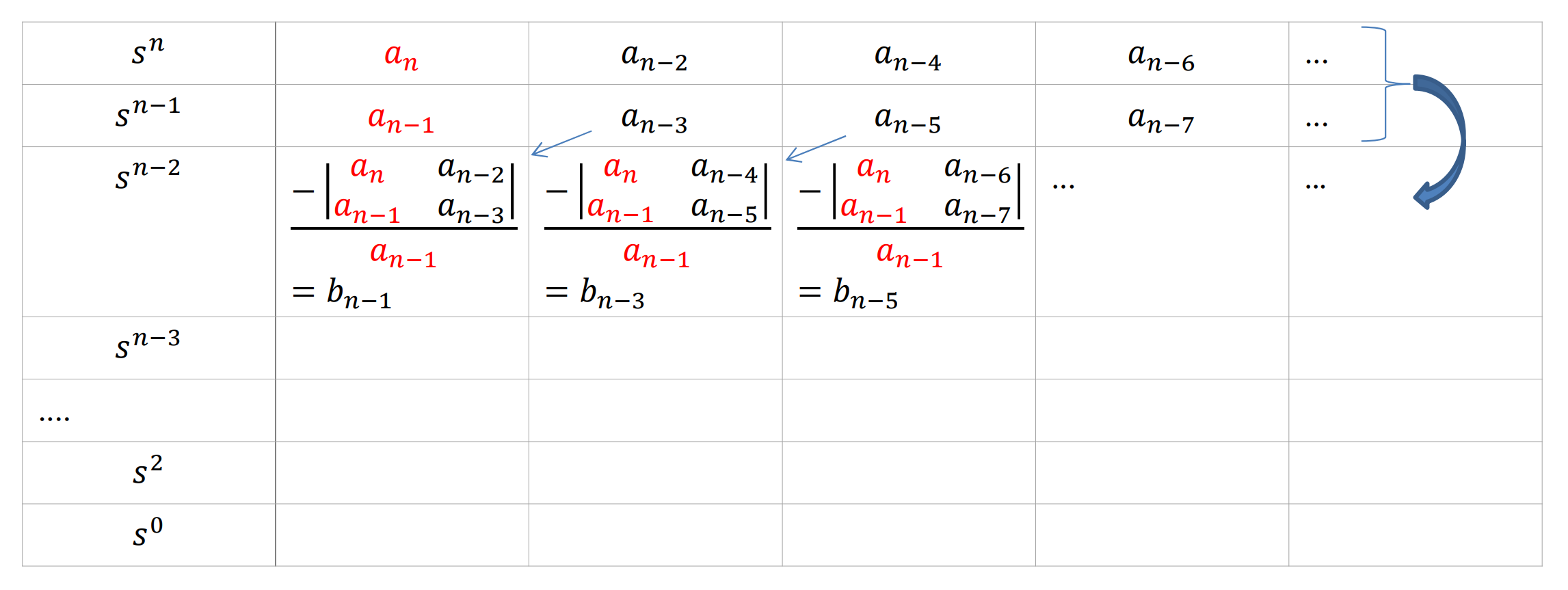
위와같은 방식으로 S^(n-3), S^(n-4)....S^2, S 번째 열까지 테이블을 완성시켜주면 된다.

위의 테이블에서,
아래처럼 1열의 Coefficient를 보면 되는데,

시스템이 안정하기 위해서는, 첫번째열 수의 부호변화가 없어야 하며, (필요충분조건)
부호변화의 횟수만큼 System Pole이 오른쪽에 위치하는 것이라 판단할 수 있다.
여기까지알고 넘겨도 되는 것이면 참 행복하겠지만,
이런 Routh-Hurwitz Criterion에도 특수한 Case가 존재한다.
다음섹션에서 이를 살펴보도록 하자
◎ Routh-Hurwitz Criterion: Special cases ★
Routh-Hurwitz Criterion에서 Table의 각 수는 Determinant를 직전 열의 수로 나눈 수이다.
...그리고 수학에서 무언가를 나눌때 항상 따라오는 문제는
'분모가 0이될 때 어떻게 처리해야 하는가?'에 관한 것이다.

Routh-Hurwitz Criterion을 아래 4가지로 나누어서 해석해보도록 하자.
1. First Column에 0이 없을때
2. First Column이 0이고, 그 행에서 나머지 열은 0이 아닐때,
3. First Column이 0인데, 그 행에서 나머지 열들이 모두 0일때. (Even Polynomial)
4. 3번 케이스와 같으나 (Even Polynomial), imaginary Axis위에 Repeated Pole이 존재할때.
○ 1. First Column에 0이 없을때
특수한 경우가 아니기에,
그저 First Column의 Sign Change의 횟수만 세주고, 이에따라 LHS여부를 판단해주면 된다.
Example)

이에따라 Table을 그려보면,
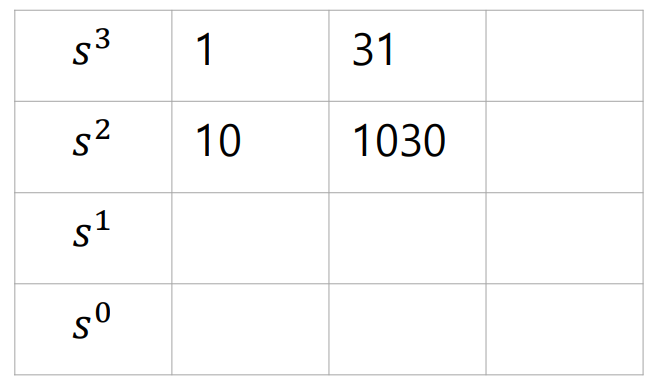
테이블에서, Pole의 Actual한 Position을 판단하는 것이아니라, 영역을 판단, 즉, Sign Change여부만 따지는 것이므로,
특정 행에 Constant를 곱하거나 나누어도 결과엔 영향이가지 않는다.
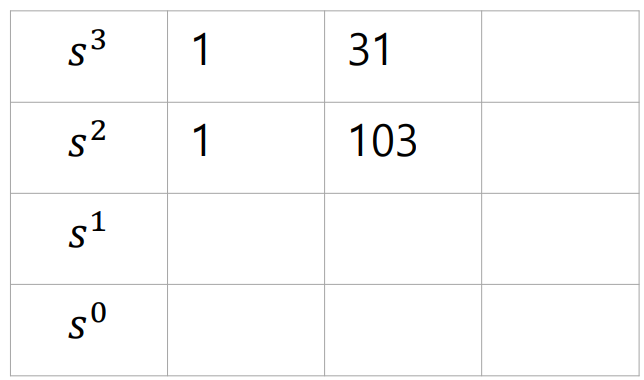

위의예시에서, 2번의 Sign Change가 있었다. 즉,
2개의 Pole이 RHP에 존재한다고 해석할 수 있다.
○ 2. First Column이 0이고, 그 행에서 나머지 열은 0이 아닐때,
이런경우, 책에서는 두가지 해결법을 다룬다.
- 첫번째 해결법. 기호를 도입하여 해결한다.
0대신 아주 작은 수를 의미하는 ε를 이용해서 표기하는데, 이에대한 내용은 아래와 같다.
example)
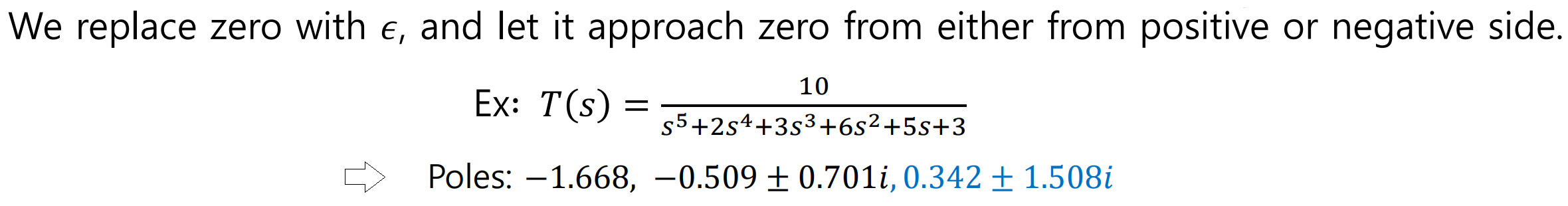
위의 시스템 식에서, 2개의 Pole이 RHP인 것을 알 수 있다.
Routh Table에서도 그러한지 살펴보자

여기서, ε의 부호를 따져보자.

확인결과, ε가 양수, 음수일때 보두 Sign Change가 두번일어나므로,
RHP에 두개의 Pole이 존재한다. 즉, 결과와 일치하는 것을 확인할 수 있다.
- 두번째 해결법, Coefficient 를 Reverse해준다.
무슨말이냐하면....
아래와같은 과정을 살펴보자,
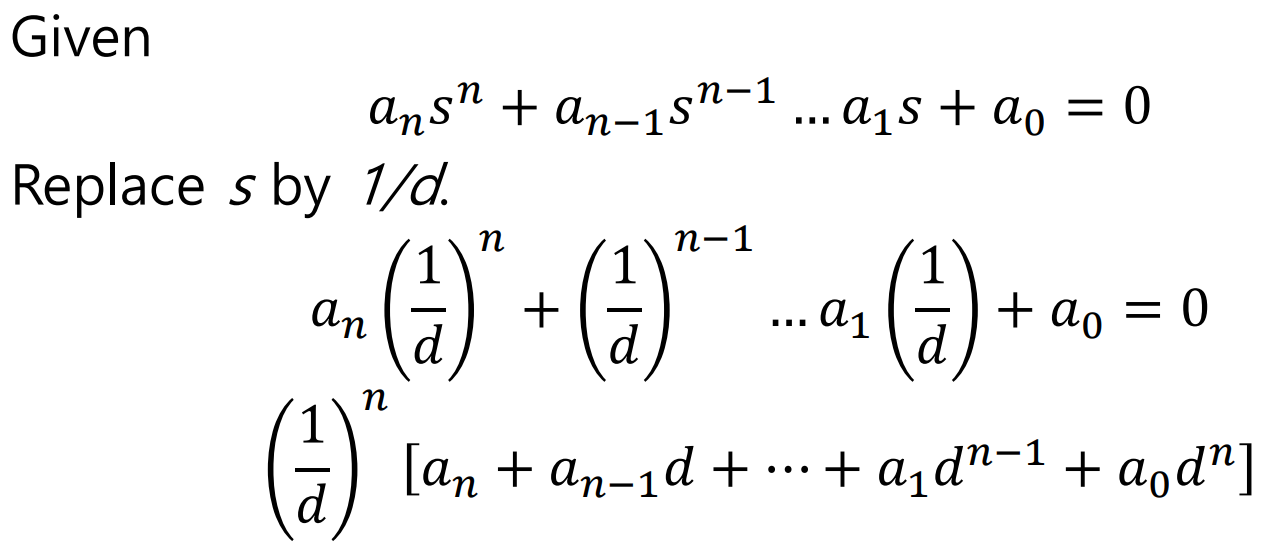
위처럼 s를 1/d로 바꿔준다고 해서 Sign Change의 변화가 있는것은 아니기 때문에,
결과는 똑같이 해석가능하다.
example)
첫번째 방법에서 쓴 TF와 동일한 TF를 가져와서 보면,
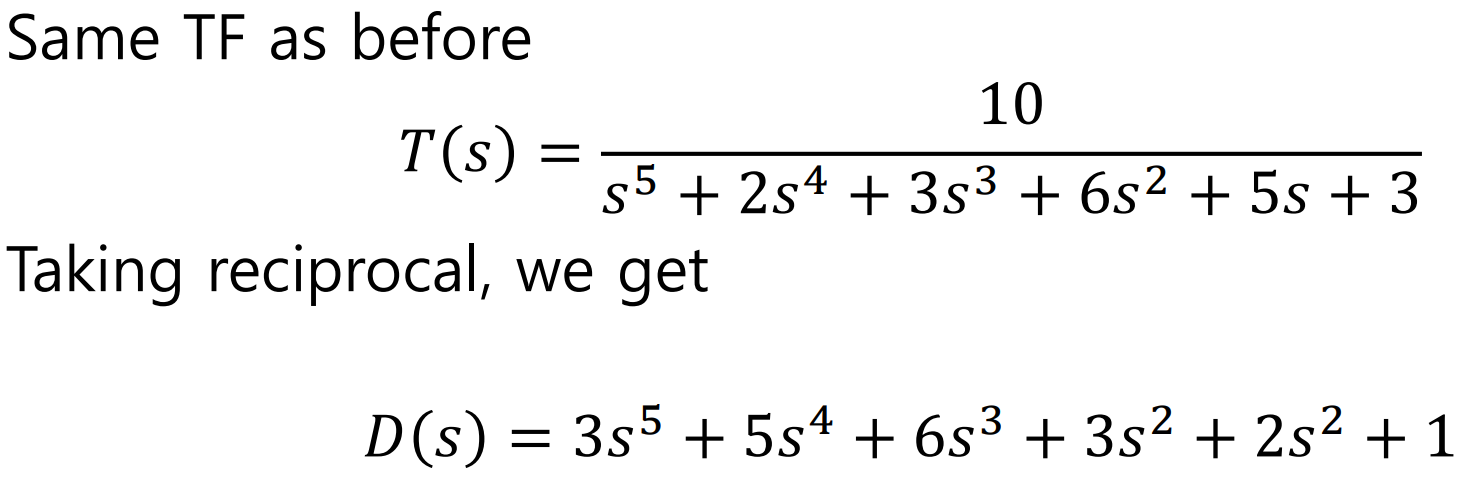
Coefficient를 Reverse해준 D(s)의 Routh Table을 그려보자.
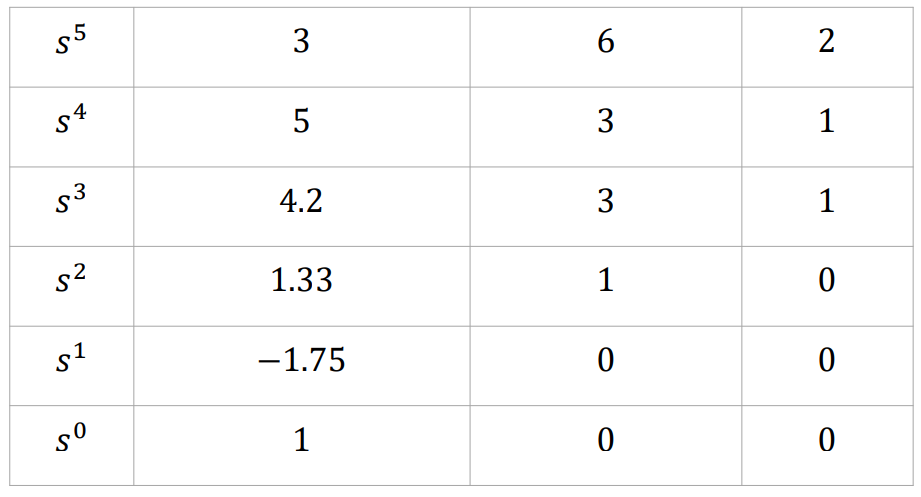
2개의 RHP Pole. 즉, 결과는 같다
○ 3. First Column이 0인데, 그 행에서 나머지 열들이 모두 0일때.
이 말인 즉, 해당 row가 모두 0이라는 말과 같으며,
곧, 원래의 Origin Polynomial식이 "Even Polynomial Factor"를 포함하고 있다는 말과 필요충분조건이된다.
(그래야 하나의 row가 모두 0이되기 때문이다)
여기서
"Even Polynomial Factor"의 뜻은, 지수가 모두 짝수인 Polynomial Equation을 의미하는데,
예를 들어
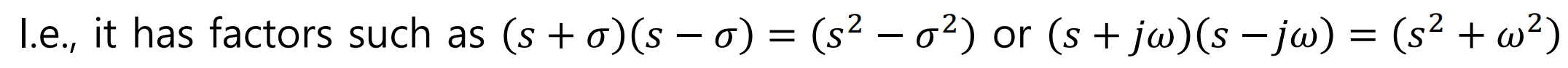
이런식을 말한다.....-> 즉, Symmetrix Root Pair, Symmetric Pole Pair를 가진다.
이런 Routh Table이 그려지는 경우에, 이를 해결하려면
Auxiliary Polynomial(보조방정식)을 Zero Entry Row대신 넣어줘야 하는데,
이때 Auxiliary Polynomial의 차수는,
Symmetric Root Pairs의 개수와 같다.(예를 들어 위에서 s^2+w^2의 Symmetric Root pair의 개수는 2개이다)
정확히 무슨말인지 아래 예시를 통해 보도록 하자.

이를 보면 알 수 있듯, S^4, S^5 Entry를 이용해 만든 S^3 Entry는 모든 Coefficient가 0이다.
여기서, Auxiliary Polynomial의 Coefficient는 S^4의 차수와 같고,
Polynomial을 이용해 아래의 과정을 거쳐 S^3에 넣어주면,
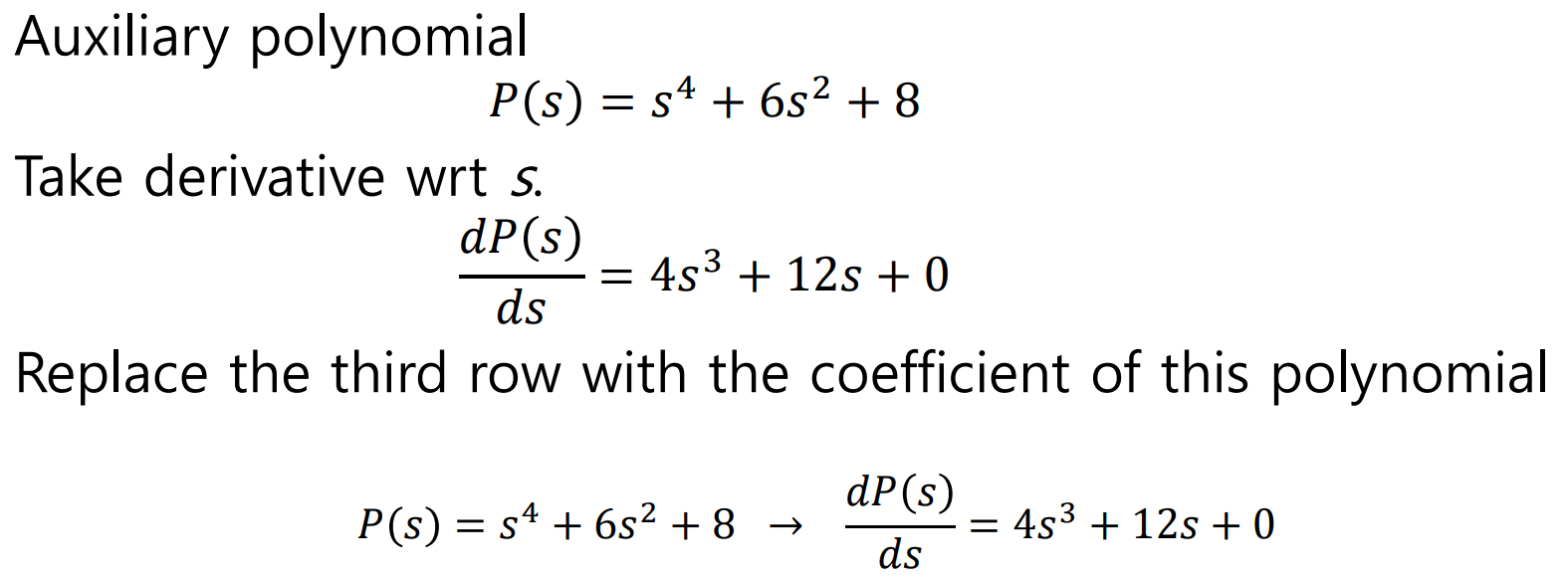
즉,

이제 이를 이용해 쭉 Routh Table을 정리해보면
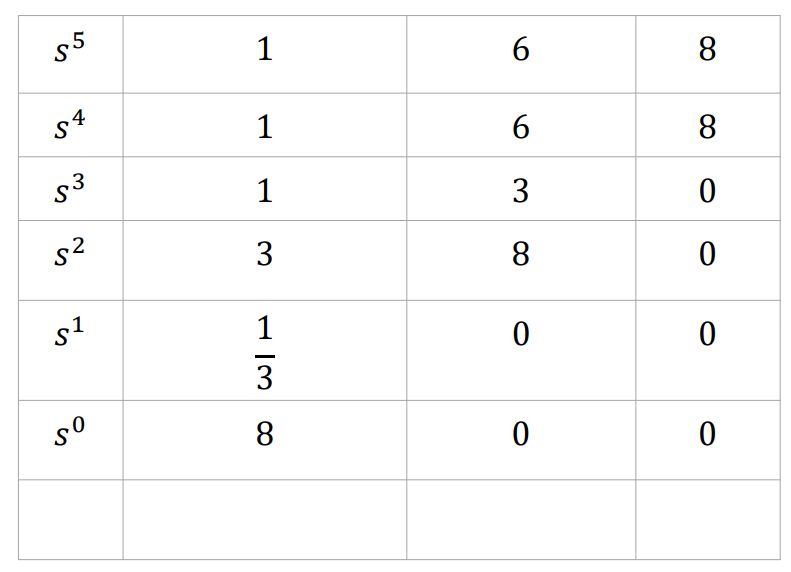
새롭게 만들어진 Routh Table은 0 Entry는 존재하지않으며,
Sign Change또한 없다. 즉, RHP에는 Pole이 존재하지 않는 시스템이다.
* RHP에 존재하지 않는 시스템이라고 해서 안정한 시스템이라고 단정지을 수 없다.
이점을 간과하지 말자.
○Even Polynomial Factors
여기서 활용된 Even Polynomial Factors에대해 좀더 자세히 살펴보도록 하자.
Even Polynomials의 Pole은, 잠깐 생각해보면 알겠지만 Origin에 대해 Symmetric한 쌍(Pair)을 갖는다.
제곱의 형태로 근을 취하기 때문이다.
케이스를 굳이 나눠보면,
아래와같이

Real Axis위에서 Symmetric한 경우, Imaginary Axis위에서 Symmetric한 경우,
그리고 축이아닌곳에 놓인경우 3가지경우로 나뉜다.
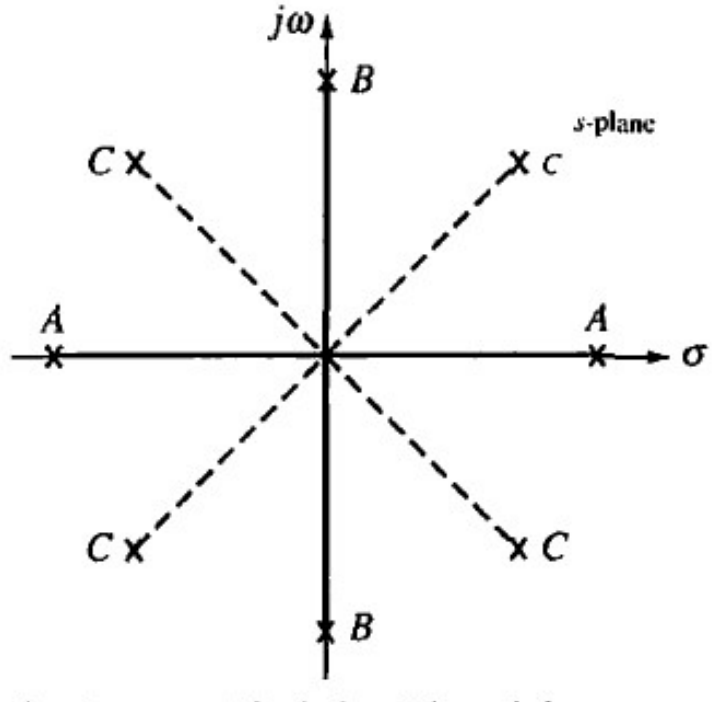
그리고, Symmetric한 Pole을 가지기 때문에,
RHP에 Pole이 놓여있지 않을 조건은 오직 한가지 경우,
두개의 Pole이 모두 imaginary Axis위에 놓인경우만 이에 해당하게 된다.
아래의 예시를 살펴보자.
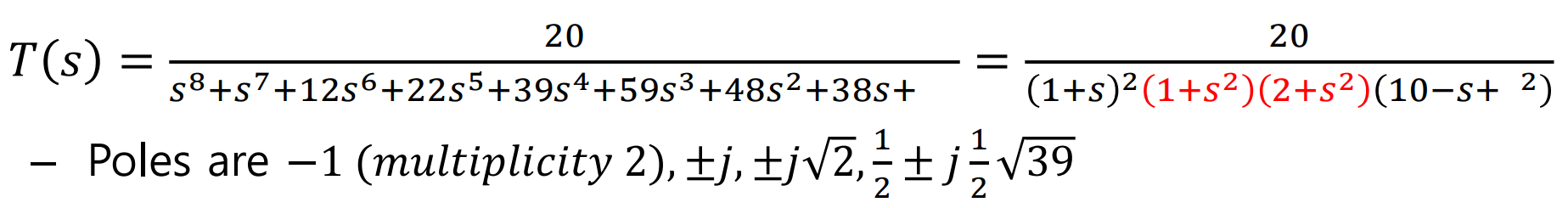
위에서 Even Polynomial은 (1+s^2)(2+s^2)이다.
Routh Table에 이를 넣어보면
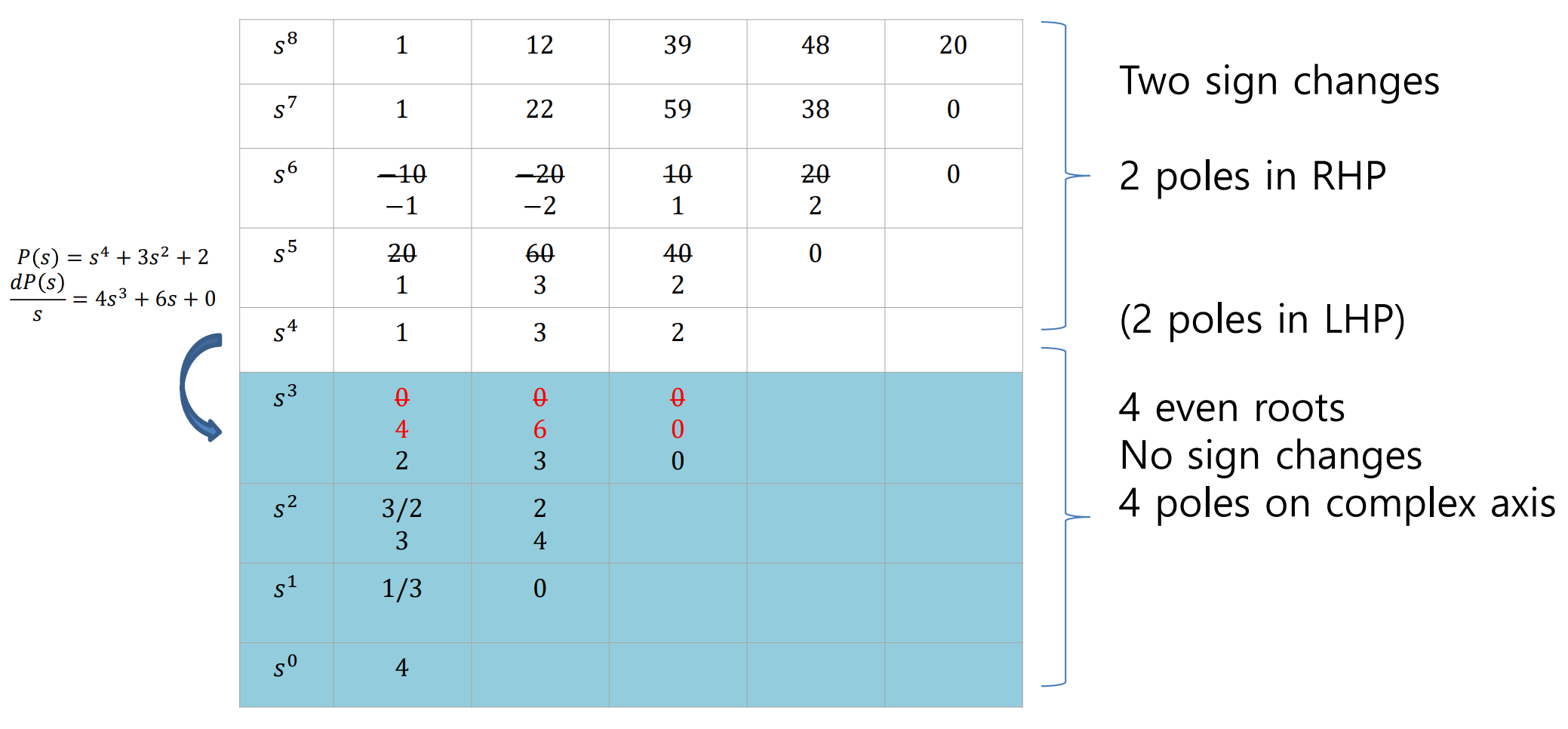
Even Polynomial 의 차수가 S^4이기 때문에,
S^3에 해당하는 Entry는 모두 0이라는 걸 알 수 있다.
이에 Auxiliary Polynomial을 미분한 계수를 S^3 Entry에 넣고 계산을 이어가면 되는데,
위의 그림에서 알 수 있듯, Auxiliary Polynomial식 아래로 sign Change가 없기때문에,
4개의 Pole(4개의 Even Polynomial의 Pole)모두 RHS에 존재하지 않으며, 각각 2쌍씩 Symmetric하다.
즉, 결과적으로 Even Polynomial의 4개의 Pole은 모두 imaginary Axis위에 놓여있음을 알 수 있다.
한번더 위 내용을 정리해보면 다음과 같다.
- Routh Table에서 Even Polynomial은 Zero Rows위에 나타난다.
- Even Polynomial에 해당하는 Row 부터 Routh Table의 끝 Row까지는
Even Polynomial Factor에 대한 Routh Table이라고 생각할 수 있는데,
이것의 Sign Change횟수는 RHP Pole의 개수와 같고, Symmetric한 LHP의 개수와도 같다.
만일 Sign Change가 없다면 imaginary Axis위에 Symmetric Pole이 존재한다고 생각할 수 있다.(Complex Root)

○ 4. 3번 케이스와 같으나 (Even Polynomial), imaginary Axis위에 Repeated Pole이 존재할때.
마지막 Case다.
Even Polynomial Factor의 Solution을 구할때, Sign Change가 없다면 모든 Pole은
Symmetric하게 Imaginary Axis위에 놓인다고 했었다.
만약 Imaginary Axis위에 놓인 Pole이 동일하게 겹쳐있다면 그때의 System의 거동은 어떻게될까?
이는
RHP에 존재하지 않는다고 해서 반드시 시스템이 Stable하다고 할 수 있을까?-> NO
에 대한 이유를 알 수 있게되는 질문이기도 하다.
아래와같은 예시를 보도록 하자.
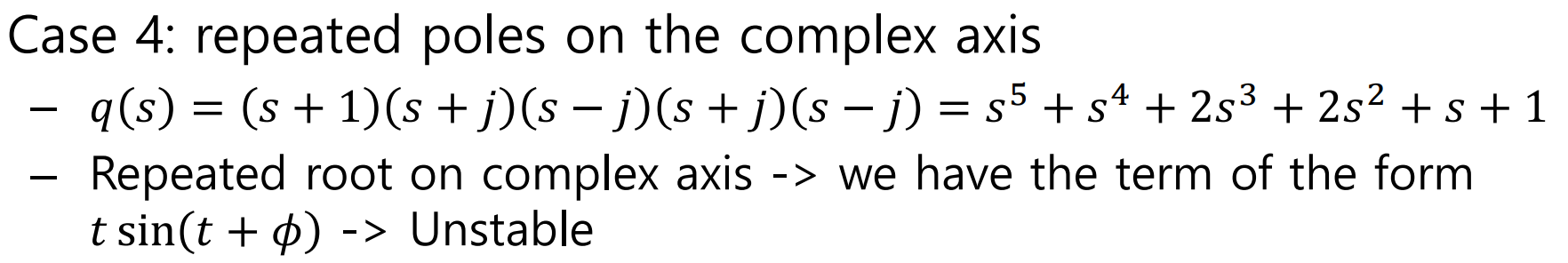
'Repeated'되어있는 Pole은 S domain에서 (S+a^2)^2또는 ^4 ..^6 등의 모습이 되는데,
이것을 Laplace Transformation하여 Time Domain에서 살펴보면, (S+a^2)일때와달리,
Envelope가 발산하는 것을 알 수 있다.
즉, 아래와같은 모양이 된다.
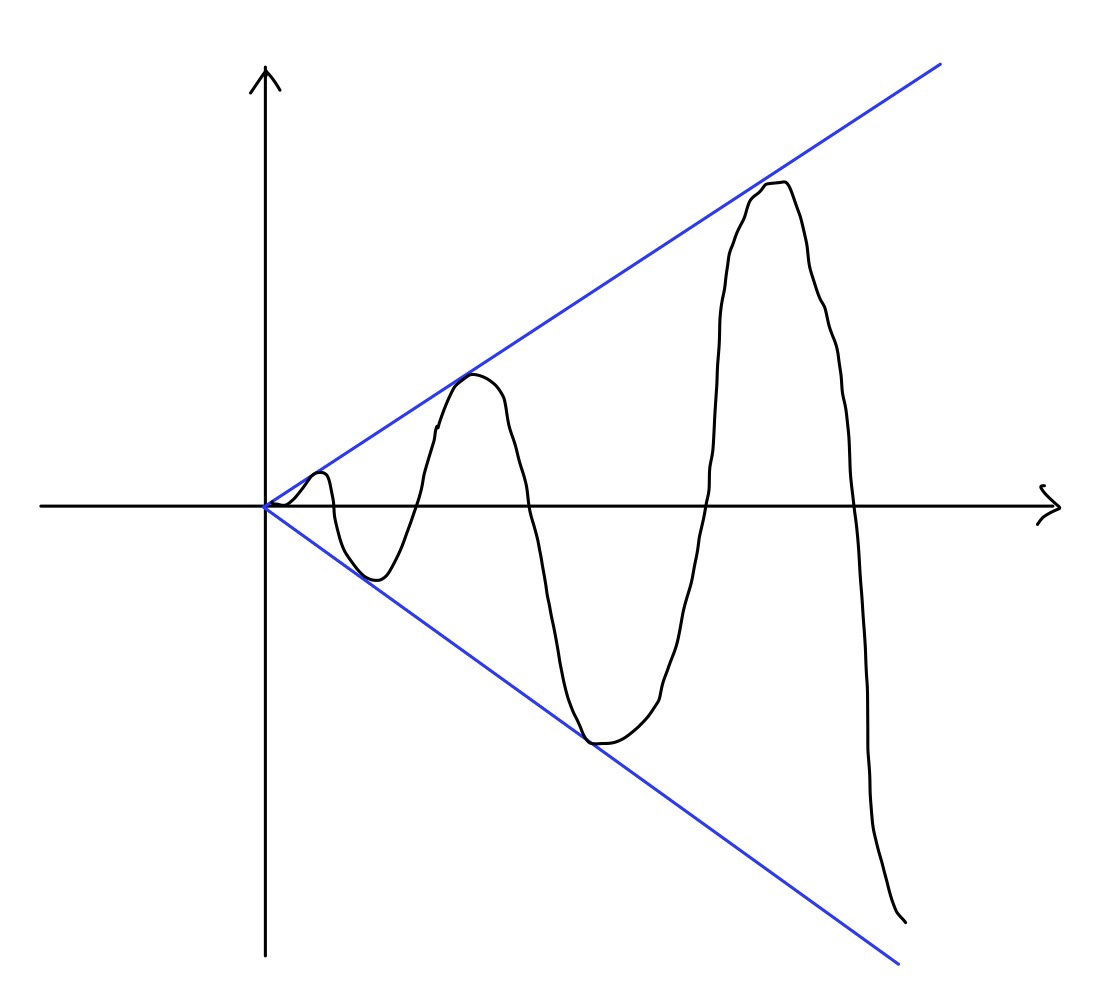
* 단, 여기서 헷갈리지 말아야 할 것은, Even Polynomial 아래가 모두 sign Change가 없다고 해서,
그것이 imaginary Axis위에 Pole이 놓인다는 것을 의미할지 몰라도 Repeated Pole임을 의미하진 않는다는 것이다.
이에대해서 책에서는 자세한 언급을 하지만,
수업에서는 결론정도만 다루었기에, 여기서도 이정도 정리만 하고 Case 4는 더 살펴보지 않겠다.
○Routh Table의 한계
Routh Table은 어디까지나 Pole이 존재하고있는 영역을 판단하기위한 하나의 '도구'로서,
실제 Pole을 구하지 못하기에 실제 시스템의 거동에대해서는 그저 안정한지 정도만 판단할 수 있을뿐,
그 이상의 정보를 얻지못한다는 한계가 있다.
또, Routh Table의 치명적인 한계가 또한가지 있는데, 바로 'marginally Stable'에 대한 판단이다.
Case4처럼, Routh Table에서 Even Polynomial아래의 Sign Change가 없다고 하더라도,
이것이 Repeated되어있는지, 각자 따로 존재하는지 Table상으로는 바로 알 수가 없다.
이말인 즉, imaginary Axis위에서 No Repeated 하여 'Marginally Stable'한건지,
아니면 Repeated되어 Envelope가 발산하는 'Unstable'싱태인지 Routh Table만으로는 판단이 불가능 하나는 말이된다.
*사실 Routh Table은 과거 컴퓨터가 없었을때 제어공학자들이 쓰던 기법으로서,
컴퓨터가 고도로 발달한 현대에 와서는 함수몇번 넣고 돌리면 컴퓨터가 알아서 파라미터에 따른 Pole을 빠르고 정확하게 구해주는데 Routh Table을 굳이 쓸 이유는 없긴하다.
(그러네... 공부왜했ㅈ..)
◎ Relative Stability
지금까지 다룬 Stability는 'Absolute Stability', 즉, 주어진 Closed Loop System이 Stable한가 아닌가에대한 판단으로,
Pole이 LHP에 놓여있는가?. imaginary Axis위에 있다면, 'Marginally Stable'한가 아니면 'Unstable'한가?
에 대한 내용이다.
여기서 다뤄볼 것은
상대적 안정성, 'Relative Stability'로, Characteristic Equation의 각 Root간 상대적인 Damping에 대한 것을 의미한다
-> 또는 , 얼마나 imaginary axis로부터 Pole이 멀리 떨어져 있는가?에 관한 내용이다.
말은 복잡한데, 그냥 Pole의 Real part가 왼쪽에있냐 오른쪽에 있냐에 관한 내용이다.
당연히 왼쪽에 있을수록(imaginary Axis에 멀어질 수록) 더 안정하고,
오른쪽에 있을수록(imaginary Axis에 가까워질 수록) 더 불안정하다.

여기서, 시스템이 안정해지려면, imaginary Axis가 더 오른쪽에 위치하도록 시스템을 조절하면 된다.

예시를 통해 자세히 살펴보자
ex) Axis Shift

보고 응 그렇구나 하면 된다.
위의 q(s)에서 Axis Shif를 적용하면
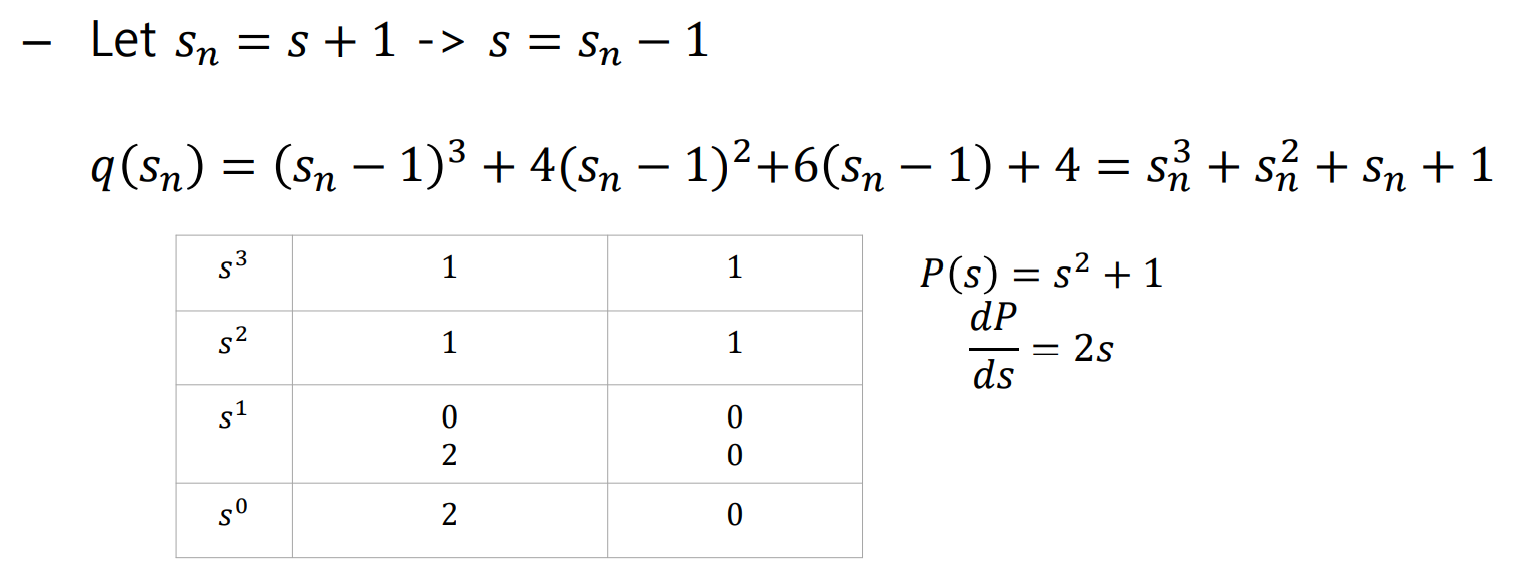
◎ Stability in state space
예전 포스팅에서 State Space 에 대해서 자세히 다뤄둔 적이 있었다.(state Space Variables )
이번 포스팅에서 주구장창 다뤘던 Stability를 이런 State Space Equation에 적용하면 어떻게 해석할 수 있을까?
*여기서도 결론만 알고 넘어가자
아래와같은 State Space Equation을 가진 System이 있다고 가정할때,
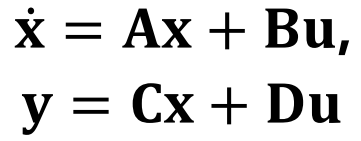
이것의 Transfer Function은
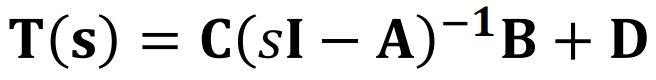
이었다. (state Space Variables 포스팅 참고)
즉, 여기서 C,B,D는 Coefficient이므로,
Characteristri Equation은
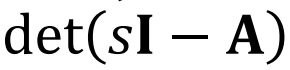
이되므로,
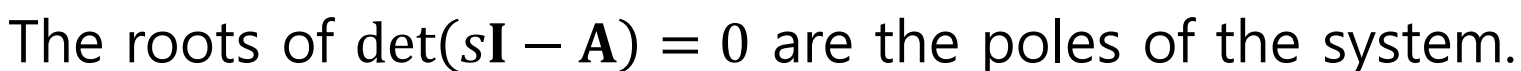
이다.
-> 여기서 쪼끔더 고급지게 이를 표현하면,
System Matrix인 A의 Eigenvalues가 곧 System의 Pole이 된다고 표현할 수 있다.
예시는 아래와 같다.
example)
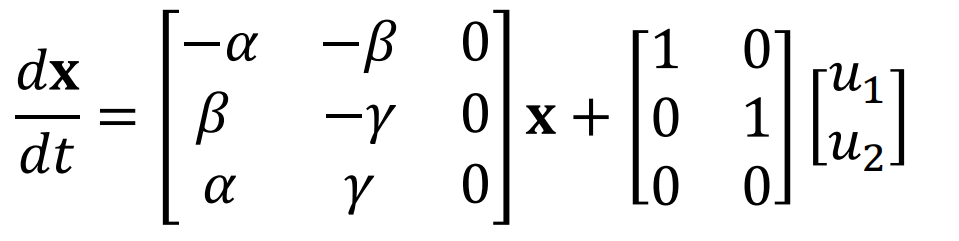
위와같은 State Space Equation에서, System matrix부분을 이용해
특성방정식을 뽑아내면
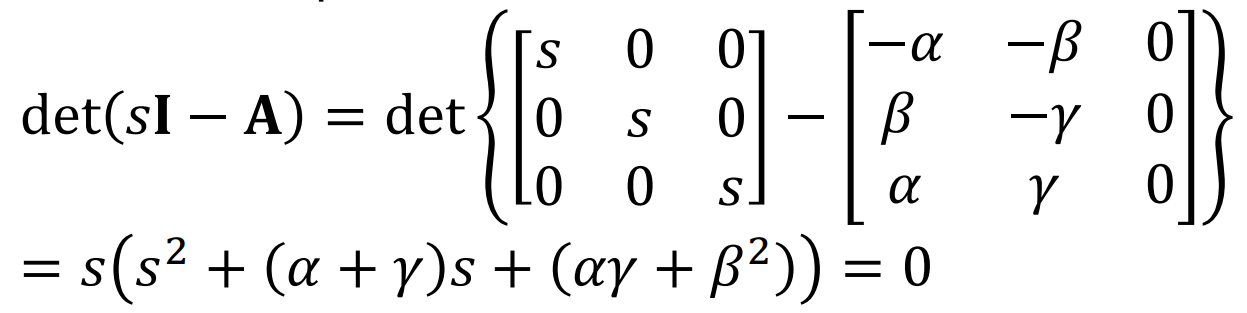
여기서,
맨앞에 곱해진 integrator S는 origin Pole로, 시스템이 Stable한지 Unstable한지에 대해 영향을 미치지 못하므로,

이 식을 위에서 주구장창 했던것 처럼 Routh Table에 넣고 시스템의 안정도를 판단해주면 된다.
이번 포스팅은 여기까지 마치도록 하겠다.
이상 System의 Stability에관한 내용이었다.
* 자세한 Exmaple들은 추후에 따로 정리할 예정
'Control > 자동제어' 카테고리의 다른 글
| The Root Locus(2) (0) | 2021.12.03 |
|---|---|
| The Root Locus(1) (0) | 2021.12.03 |
| The Performance of Feedback Control Systems (2) (0) | 2021.11.13 |
| The Performance of Feedback Control Systems (1) (0) | 2021.11.12 |
| State Space Variables(2) (0) | 2021.10.17 |




