정리노트
The Root Locus(2) 본문
이번 포스팅에서는 Root Locus를 어떻게 그려야하는지에대해
자세히 다뤄보고자 한다.
앞선 포스팅에서 말했듯, 단순히 한점의 Pole을 가지고 이야기 하는 것이아닌,
Pole이 놓이는 연속적인 점들에대한 해석을 다루기 때문에, 알고 넘어가야하는 것들이 다소 많은편이다.
◆ 목차: Precedure of the Root Locus + Refining Sketch ★
○ Step 1 : Write the Characteristic Equation
○ Step 2: Real Axis 위에 놓인 Pole 판단
○ Step 3: Loci가 따라가는 점근선(Asymptote) : to infinity Zero
○ Step 4 : Locus가 imaginary Axis위를 지나는지 판단 (by Routh–Hurwitz criterion)
○ Step 5: Real Axis에서, Break away Point와 Break In Point 구분
○ Step 6: Root Locue(Branch)의 출발 각도
○ Step 7: Complete Sketch
Precedure of the Root Locus + Refining Sketch
Root Locus를 그리는 절차에 대해 다루기전에, 먼저 알아두어야할 내용에대해 정리해보며 시작해보자.
- Root Locus는 Pole의 Locus를 말한다(?)...(..책의 표현인데...Locus는 번역하면 '장소,위치'라는 뜻이라고 한다..)
- 이전 포스팅에서 살펴본 System에서는 K의 값 하나에 대응되는 Pole이 두개였는데,
이렇게 K 하나의 변화당 여러개로 나누어진 Pole의 경로를 'Branch'라고 하고, 이는 P(s)의 Pole의 개수와 같다.
- Root Loci(Loci는 Locus의 복수... 그냥 Locus로 해석하면 될듯하다)는 Real Axis에대해 Symmetric하다.
이제 본격적으로 Procedure에 대해 살펴보자.
○ Step 1 : Write the Characteristic Equation
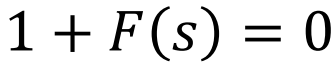
여기서 F(s)가 가지고있는 System Parameter에대해 정리해주면


즉,


위와같은 식으로 정리된다.
여기서, K가 0에서부터 무한대로 갈때 각각 식이 어떻게 변하는지 살펴보면..
먼저 K =0에 가까워질때,
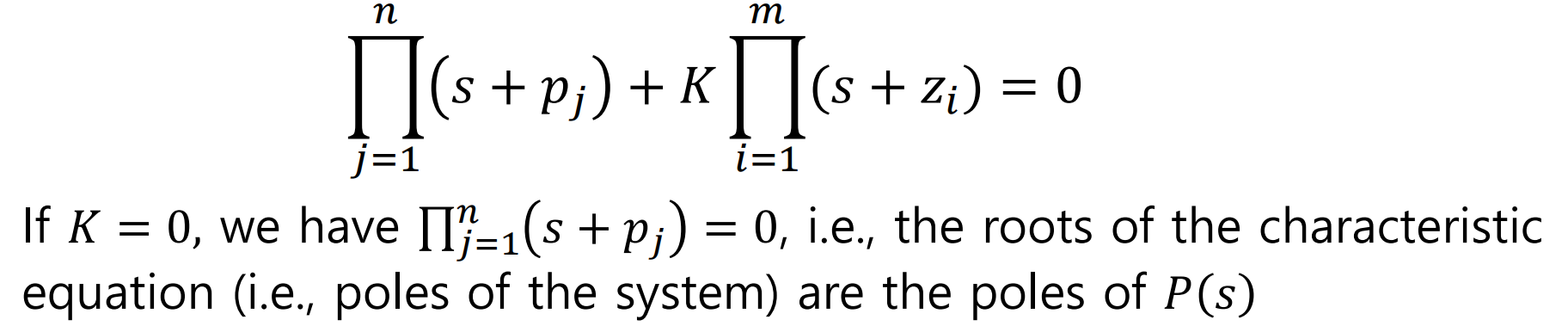
System의 Pole은 P(s)의 Pole과 가까워진다
반대로, K = 무한대 에 가까워지면,
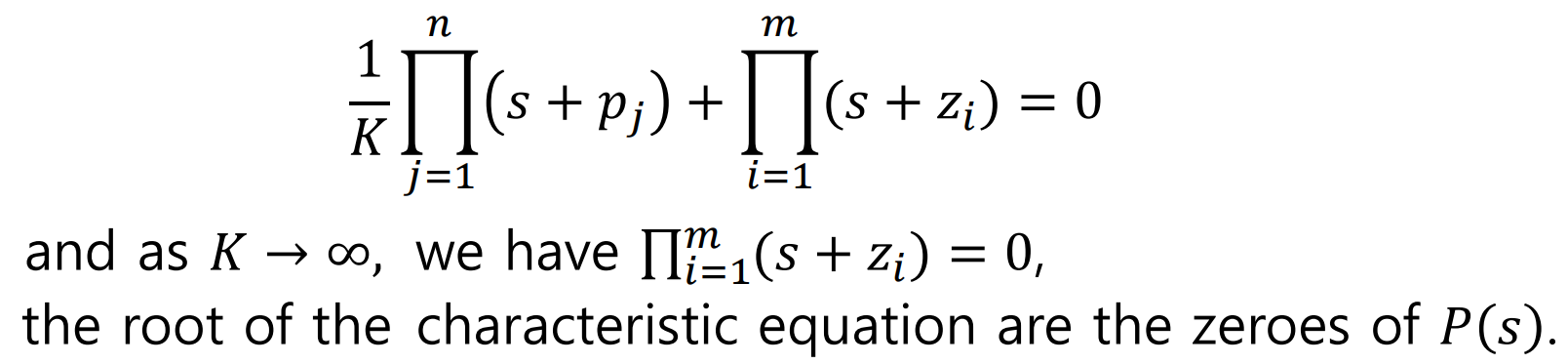
System의 Pole은 P(s)의 Zero과 가까워진다
조금 Rough하게 위에서의 결론을 이야기하면,
K가 증가함에 따라 Root Locus는 P(s)의 Pole에서 Zero 방향으로 이동한다고 할 수 있다.

* 조심해야할 부분은, 앞서도 언급했지만, P(s)는 전체 Closed FeedBack System의 Characteristice Equation이 아니라는점이다. 헷갈리지 않도록 하자.
여기서 한가지 더 짚고 넘어가야할 것이 있다.
바로 Pole의 개수와 Zero개수이다.
Pole의 개수를 n, Zero의 개수를 m이라고 하자. n>m이라고 가정할 때,
(강의에서 n<m인경우는 다루지 않으며, 실제 다뤄야할 시스템 대부분도 n>m이라고 한다.
그렇기때문에 n<m인 케이스는 따로 다루지 않겠다.)

분모의 차수가 분자의 차수보다 크므로, s가 무한대로 감에 따라 P(s)는 0에수렴한다.
P(∞) = 0이라는것의 의미는 곧 System의 'Zero'와 그 의미가 같다.
즉... "s = ∞에 위치에 System의 zero가 존재한다" 라고 해석이 가능하며,
이 무한대의 지점에 존재하는 Zero를 infinity Zero라 하고, 그 개수는 n-m개가 된다.
-> zero의개수 + infinity Zero의 개수 = Pole의 개수 = branch의 개수
○ Step 2: Real Axis 위에 놓인 Pole 판단.
위에서 다룬 예시중에, K의 범위에 따라서 S-plane상 Pole이 놓일 수 있는 위치를 구분지었었던 예시가 있었다.
Step2에서 다뤄볼 내용도 이와 비슷한데,
S-Plane상에 P(s)의 Pole, Zero가 주어졌을 때, Real line을 지나는 Pole은 어디에 위치해야 하는가? 에 관한 내용이다.
앞서서, Closed Loop Feedback System의 특성방정식이 0이되기 위해서,
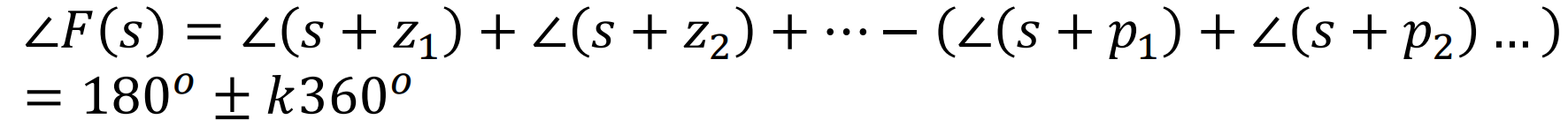
Zero의 Phasor각 합에서 Pole의 Phasor각 합을 뺀 값이 180(1+2k)도이어야 한다고 했었다.
이 조건을 여기에서도 이용하게 되는데,
결론부터 이야기하면,
Root Locus의 Real Axis 값보다 오른쪽에 Pole+zero의 개수가 홀수개인 곳에Root Locus가 위치하게되며,
짝수개인 곳에는 존재할 수가 없다

왜 그럴까?

위의 그림을 보고 생각해보자.
먼저, Real Axis 상의 Root Locus값과 그 왼쪽에 있는 P(s)의 Pole과 Zero가 아루는 각도는 모두 0이다.
그래서 위의 조건에 고려사항에서 배제해도 상관없다.우리가 봐야할 부분은 바로 오른쪽에 있는 부분들이다.
만약 그 오른쪽에 짝수개의 Pole, Zero 가 있다면 Root Locus를 그리는 조건식
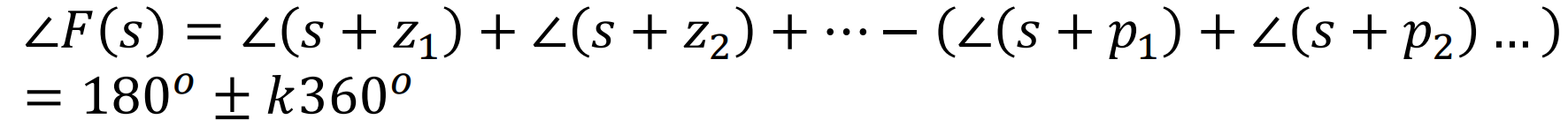
이 성립할 수 없다. 왜냐고 묻는다면.........직접해보면 알아요(0도 ,360도, 720도 이런식으로 Phasor각들이 잡히기때문)
오른쪽에 홀수개의 Pole과 Zero가 존재해야만 Root Locus 조건식을 만족하여F(s) = -1 , 180도가 된다.
예시를 통해 이를 적용해보도록 하자.

즉,

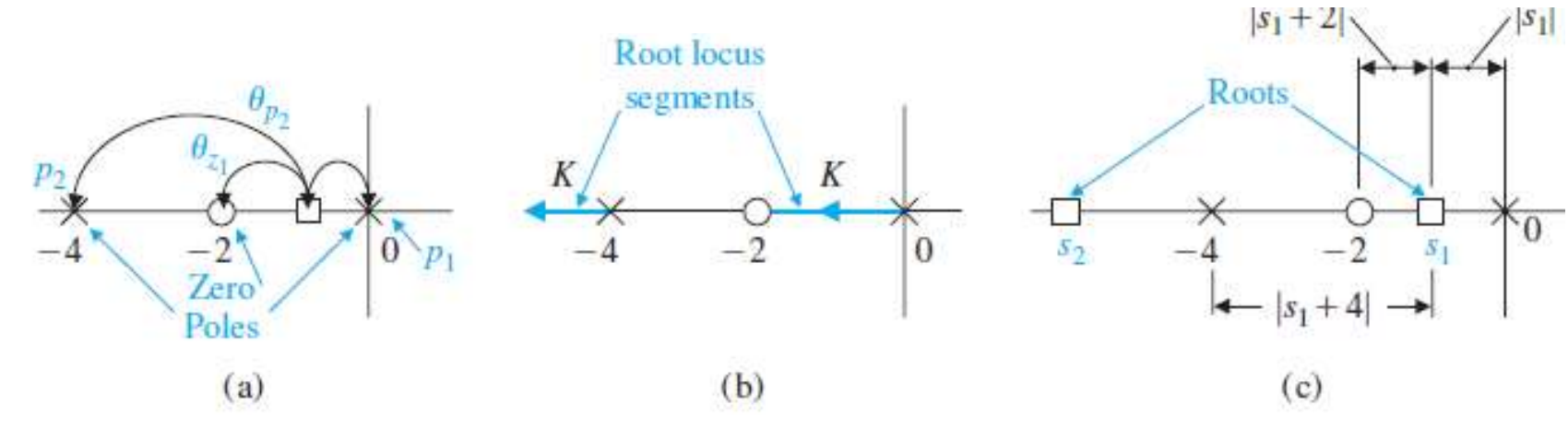
P(s)의 모두 실수인 Pole과 Zero를 S-Plane상에 위치시키고, Step2를 적용시켜서
Real Axis상에 Root Locus가 어느곳에 위치해야 하는지 판단하고,
Step1을 이용해 Pole -> Zero로 Branches의 방향을 정하여 Root Locus를 그린다.
그리고, K의 값을 원하는 S에 따라서 정함으로서, System을 디자인 할 수 있게된다.
○ Step 3: K가 zero에서 infinity로 증가함에 따라 Loci가 따라가는 점근선(Asymptote)
조금전 Step1에서, Pole의 개수에서 Zero의 개수를 뺀 만큼
infinity Zero가 존재한다고 했었다.
그리고 System은 pole에서 Zero로 이동하는데, 만약 Pole의 개수가 Zero의 개수보다 많다면,
필연적으로 Loci는 무한한 지점에 있는 Zero를 따라가게 된다.
아래의 예시를 보자.
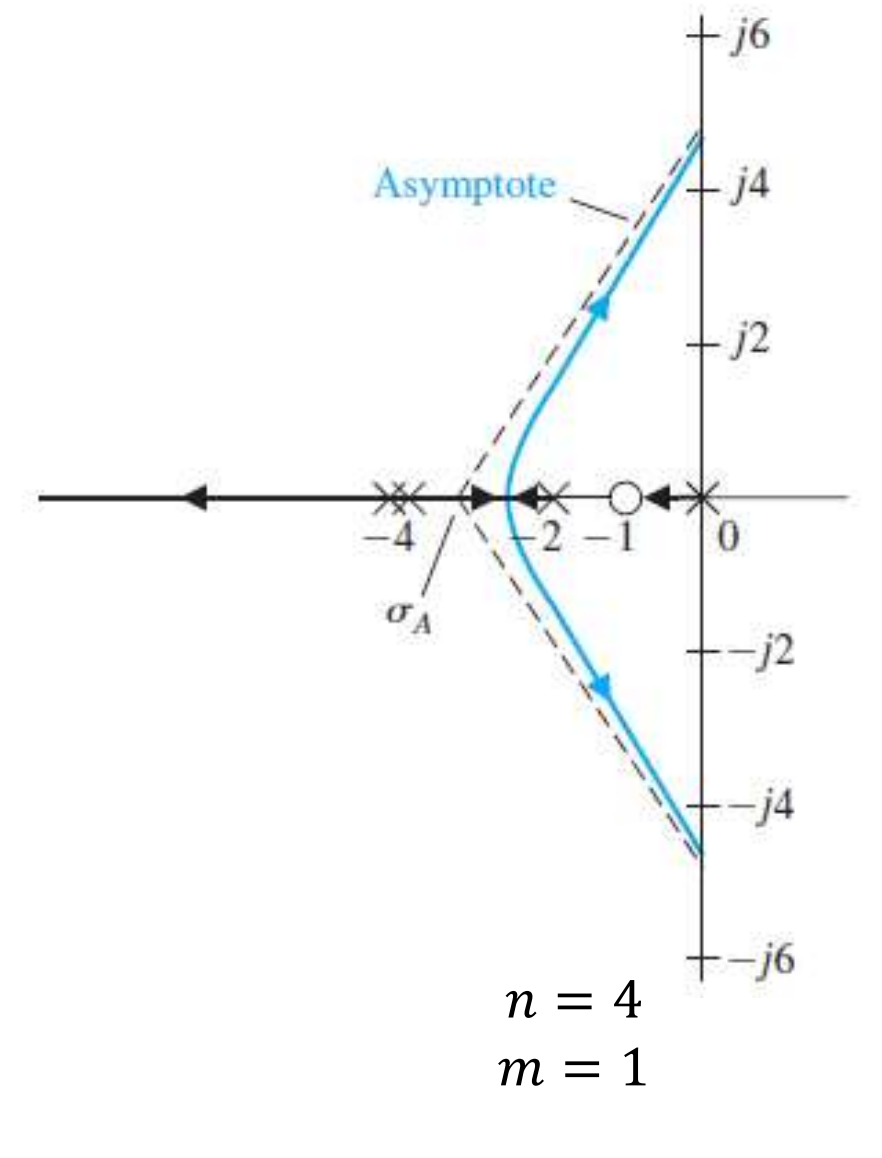
이렇게 K가 무한대로 증가함에 따라 Loci가 따라가게 되는 Asymptote(점근선)는
Real Axis에 centered 되어있고, 이때 Real Axis와 이루는 각도는 아래와 같다.
무슨말인지 아래의 식을통해 자세히 알아보자.
먼저 Centered Point가 어디인지 판단해보면 아래와 같다.
n,m을

라고 할때, Asymptote Centroid는 아래와 같다.
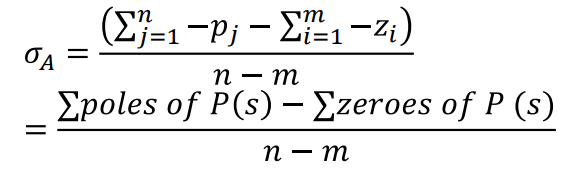
P(s)의 Pole의 위치에서 Zero의 위치를 뺀 값을, Pole의개수, Zero의 개수만큼 나눈 값을
Centroid point (Asymptote의 출발점)로 잡았다.
그리고, 이때 Asymptote가 Real Axis와 이루는 각도는 아래와 같다.
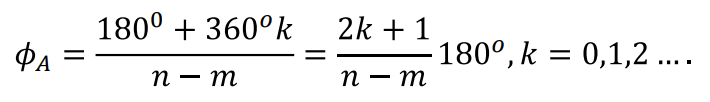
....갑자기 결론부터 나오니 뜬구름 잡는 소리 처럼 보일 수 있는데
이 두가지에대한 증명은 아래내용과 같다
먼저 Asymptote의 Angle에대한 증명부터 살펴보자.
- Asymptote의 각도공식 증명
위에서 Pole의 개수> Zero의 개수라고 하였고,
infinite Zero의 개수는 pole의 개수에서 not infinite Zero의 개수, 즉, n-m개 라고 하였다.
Asymptote(점근선)는 무한히 가깝게 접근하는 특정한 선을 말하는 것으로,
여기서는 'infinite Zero를 향해 나아가는 Root Locus가 점점 가까워 지는 선'을 말한다.
즉, 이를 다시말하면,
Root Locus에서 Asymptote, 점근선의 개수는 infinite Zero의 개수와 같으므로,
pole의 개수 - zero의 개수 와 같다.
먼저, s가 무한히 커진다면 (Infinity Zero에 가까워진다면, 그리고 K가 무한히 커진다면, 과 같은말)
P(s)의 Pole과 Zero가
Closed Loop Feedback System의 Pole과 Zero에 끼치는 영향이 거의 없어진다고 봐도 된다.

전체 시스템의 Characteristic Equation = 0이어야 하고,
이에 따라 P(s)의 Phasor는 180+(2k+1)*360이어야 한다고 하였다.
P(s)는

와 같고, 이에대한 Phasor표현은

여기서, 첫번째 Zero Term의 Phasor와, 두번째 Pole Term의 Phasor는,
infinity zero를 향해 뻗어나가는 Asymptote가 Real axis와 이루는 각도와 그 값이 같다. 즉
아래와 같이 정리된다.


- Asymptote Centroid 증명
Asymptote의
Asymptote의 중심에 대한 증명은... 여러 Approximation을 통해 증면된다..
결론만 알고 넘어가도 상관은 없긴 하겠다만, 일단 한번 다뤄보도록 하자.
우선, System Characterestic Equation에서 s(또는 k)가 무한대로 갈 때
Pole, Zero의 영향이 정말 아예없다고 가정하여,
아래와같이 정말 Rough한 Approximation을 해보자.
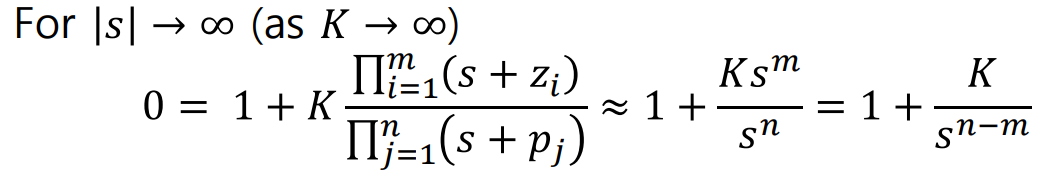
이 식의 의미는 아래와 같아진다.

즉, S=0에서 Asymptote의 Centroid가 생성되는데, 이값이 Origin값과 같다.
너무 Rough하게 Approximation하였기 때문에, Pole과 Zero가 시스템상 존재하지 않는다고 가정했을때의 RootLocus Centroid가 된다.

.. 너무 Rough하게 Approximation한 나머지
Pole, Zero상관없이 Centroid가 S=0일때로 형성됐다.
이 Rough한 Approximation을 아래와같이
한개의 항을 더 살리는 식으로 바꿔보자.
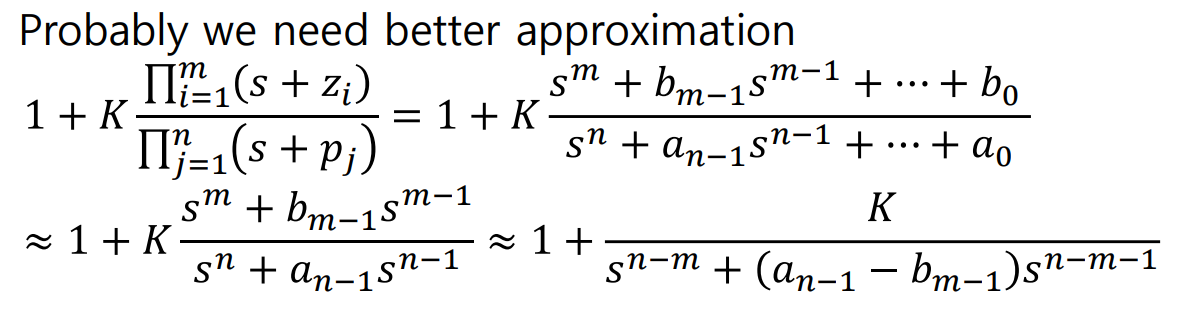
Appriximation에서 S^(m-n-1)항까지 살려주는 것이다.
이때, 최고차항 m-n에서 하나 떨어져있는 다항식의 Coefficient의 특징이 사용되는데,
아래와 같은 특성을 만족하게 된다

즉, 위의 Approximation은

로 바꿔서 표현이되는데,
아까 식에서 평행이동 한 만큼 Asymptote가 형성되므로,

에서 Asymptote가 시작되고, 이점이 Centroid가 된다.

그렇다면 저 Centroid를 어떻게 구할 수 있을까?
이것도 Approximation을 통해 구해지는데, 그 과정은 아래와같다.
위에서
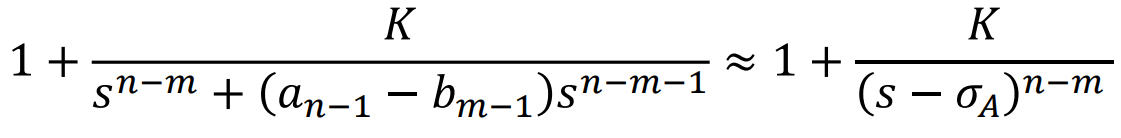
라고 하였다.
여기서 위와 똑같이 다항식의 Approximation을 적용하면

이므로,

즉,
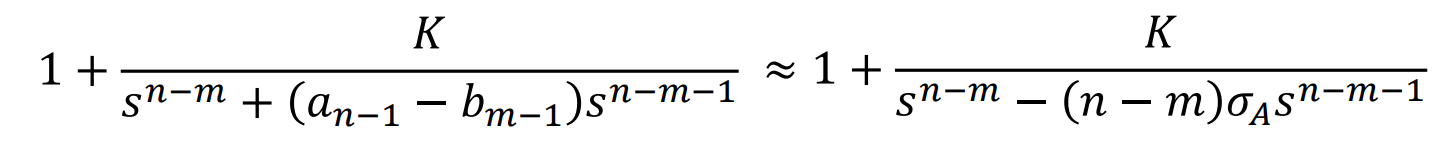
이 되므로,

이고,
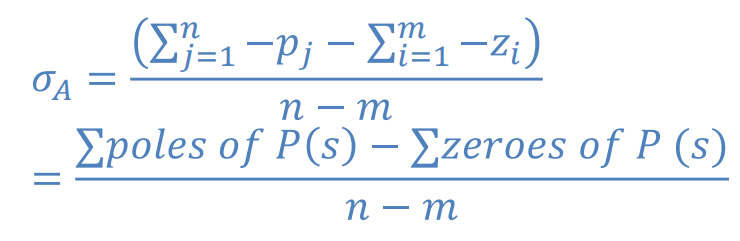
이라는 결론이 나온다.
○ Step 1,2,3 적용 Example
Example 1)
Step 1,2,3에서 다룬 내용을 아래의 예시에 적용해보도록 하자.
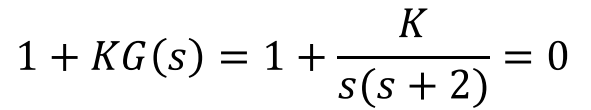
2개의 Pole, 0개의 Zero로 이루어진 이 Characteristic Equation은 아래와같이 정리할 수 있다.

여기서 Asymptote의 Center Point와 Angle을 구해보면
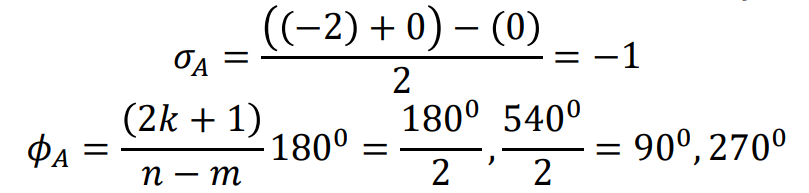
이를 Graphical하게 표현하면
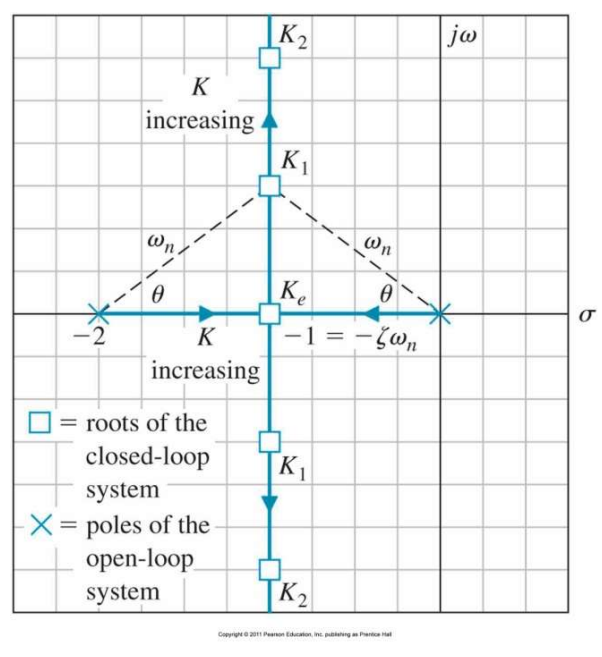
s=-2 ~ s=0 사이에 Loci가 존재하며, K의 범위에 따라 초반에는 Real Line위에 두개의 Loci가 존재했다가,
S = 1에서부터 두개의 Loci가 S = -1 수직선 위 아래방향으로 이동하게된다.
Example 2)
그 다음 예시는 조금더 복잡한 예시를 들어보도록 하자.
아래와 같은 System Characteristic Equation이 있을때
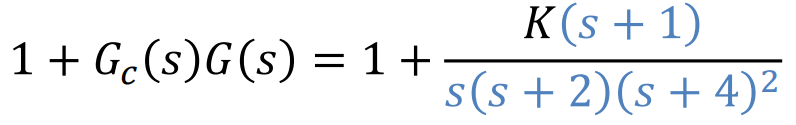
4개의 Pole과 1개의 Zero, 3개의 infinite Zero가 존재하며,
Pole중 S = -4위치에서 Repeated Pole이 존재한다.
P(s)에대해서 Graphical하게 표현하면

Asymptote의 Centroid와 Angle을 구해보면
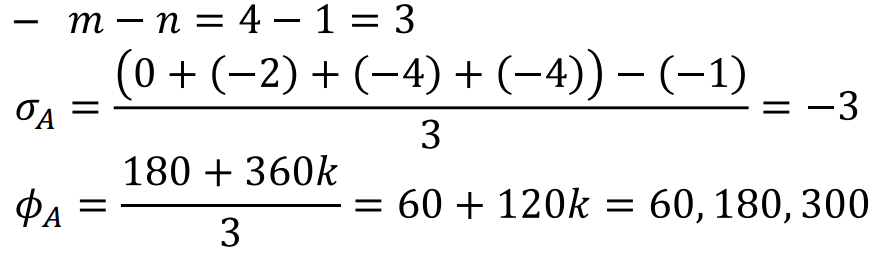
즉, 3개의 Asymptote가 존재하며, (infinite Zero의 개수와 같다)
하나는(180도) Real Axis위에,
나머지 두개는 Real Axis에서 60도 차이로 위아래로 뻗어나가는 Asymptote가 그려진다.
(Centroid는 -3으로 모두 같다)
여기서, 앞서 살펴봤던 내용을 생각해보도록 하자.
우선, K값에 따라서 정해지는 Pole의 개수는 4개이므로, Branch는 4개이다.
각각의 Loci가 어떻게 이동하는지 Graphical하게 살펴보면

Loci의 Real Axis 값보다 오른쪽에 항상 홀수개의 P(s)의 Pole + Zero 개수가 존재해야 한다고 하였다, 즉,
Locus가 존재할 수 있는 위치는
- 0 ~ -1
- -4 ~ -2
- -4 ~ -∞
이며,
Branch는 아래와같다.

이 System Pole의 거동을 다시 Locus의 Asymptote로 넘어와서 생각을 해보자.
-4부터 무한대까지 가는 Pole의 경우, (Centroid) s = -3부터 시작하여
180도각도로 뻗어나가는 Asymptote를 따라 무한히 이동하여 P(s)의 infinite zero를 향해 나아간다.
0부터 -1사이 놓인 Pole의 Asymptote는 존재하지 않고, 그 위치에 머문다.
나머지 두개의 Loci는 어떻게될까?
Asymptote중, 180도각도의 Asymptote를 제외한 나머지 두개의 Asymptote,
60도와 300도의 각도를 가진 Asymptote를 따라 남은 두개의 P(s) infinite Zero를 향해 나아간다고 해석할 수 있다.

○ Step 4 : Routh–Hurwitz criterion을 이용하여 Locus가 imaginary Axis위를 지나는지 판단
이 말인즉, LHS에서 벗어나는 Locus가 존재하는가? 를 판단하라는 이야기이며,
System이 Unstable하게되는 System Parameter K를 찾으라는 말과 같다.
만일 imaginary Axis위를 지나는 Locus가 그려진다면,
jw Axis위에 Conjugate Pole이 존재하는 그림이 되고, 즉, Routh Array에서 0이되는 Row를
찾는 과정과 같게된다. (이에대한 자세한 내용은 이전 Routh Table 포스팅에서 다루었다.)
예시를 통해 자세히 살펴보도록 하자.
Example)

이 시스템의 Transfer Function은 다음과 같다.
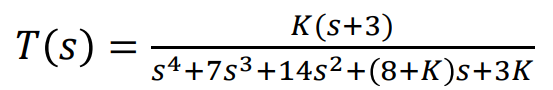
이 TF의 Routh Table을 다음과같이 그려보면

우리가 구하고자 하는 것은, K값의 범위가 0에서부터 시작해서 무한히 변함에 따라 Loci의 변화를 보려는 것이며,
이를통해 System이 언제 불안정한지 판단하려고 하는 것, 즉, Loci가 LHS를 벗어나는 지점을 찾으려고 하는 것이다.
Routh table으로 이를 구하려면,
imaginary Axis위에 Root Locus가 놓여있을때, 즉,
Row의 모든 Elements가 0인 Zero Row일때.. -> TF에 Even Polynomial Factor가 있을때
를 이용해서 이를 구할 수 있게된다.
All Zero Rows라는 것의 의미는 Even Polynomial Factor를 가지고 있는것,
즉, origin에 symmetric한 두개의 Imaginary Axis이 존재한다는 것과 같다.
(여기서 Symmetric한 이유는, 아마도 Angle Condition때문일 것이다)
(사실,
imaginary Axis위에 Pole이 존재한다
<=>
Root Locus가, LHP를 벗어나며, imary Axis위에 있는 두개의 Pole이 존재한다
이 두가지가 필요충분 조건인지에 대한 의문점이 들긴하지만,
일단 수업에서 크게 다루지 않은 부분이기도하고.. 우선 결론만 알고 넘어가도록 함...)
즉, All Zero Row를 만들기위해 s^1 Row의 First Column을 살펴보면

0보다 큰 K를 선택하고,
s^2번째 Row의 s에대한 Polynomial에서 근을 구하면,

S도메인에서의 Crossing Point를 찾을 수 있다.
○ Step 5: Real Axis에서, Break away Point와 Break In Point 구분
K에 따라 이동하는 System의 Pole의 거동, 즉 Branch는
P(s)의 Pole에서 출발하여 Zero로 이동한다고 하였다.
여러개의 Branch가 이동하는 과정에서, 한점으로 모인후 다시 이동하는 지점이 생기는데,
이때의 K값은
System Characteristic Equation이 Repeated Pole을 가지게끔하는 값이라고 생각할 수 있다.
이렇게 Branch가 중근으로 모여들었다가 다시 뻗어나가는 지점을 Break out, Break in Point라고 하는데,
Pole에서 출발해서 모여들었다가 뻗어나가는 지점을 Break Out,
Pole에서 뻗어나갔던 Branch가 다시 모여드는 지점을 Break in이라고 한다.
그리고 Break in Point에서 Branch는 각자 Zero를 향해서 다시 뻗어나간다.
앞서 봤던 Real Axis위에 놓여있을때 오른쪽에 Pole과 Zero의 개수는 홀수개가 있어야 한다는 점도 잊지말자.
..... 말로는 정말 외계어처럼 느껴지는데..
그림을 통해서 자세히 알아보도록 하자.
우선, 가장 간단한 예시로
아래의 그림처럼 System에서 2개의Pole만 있는 경우를 생각해보자.

Pole만 두개있으므로, n-m = 2, 즉 Asymptote는 2개이며, 2개의 Branch 가 infinite Zero를 향해 뻗어나간다.
그리고 이때 두 Asymptote의 Centroid는 ( (-4-2) - 0 ) / 2 = -3이며, 각도는 (180+360n)/2 = 90, 270도 이다.
(윗부분에서 다룬내용이다)
System Parameter K가 증가함에 따라 Root Locus는 P(s)의 Pole에서 출발하여 Zero로 이동한다고 하였다.
즉, 두개의 Branch의 첫 출발점은, P(s)의 두개의 Pole s=-4,-2이며,
s= -3에서 System Characteristic Equation은 중근을 갖게되어 두 Branch가 서로 만난다.
그리고 이 만나는 지점(s = -3)을 바로 'Break Away Point'라고 한다.
이런 예는 어떨까?
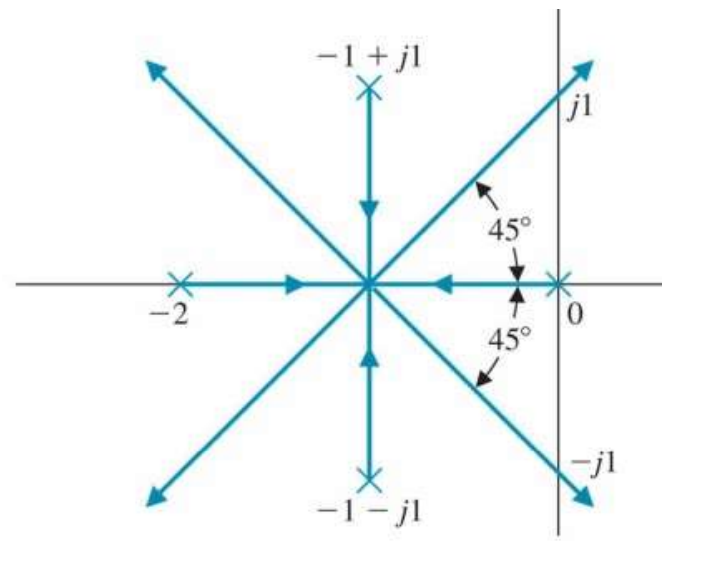
뭔가 더 복잡해보이지만,
쫄거 없다. P(s)가 4개의 Pole, 0개의 Zero일때의 예시로서,
4개의 Asymptote를 가지고,
Asymptote의 Centroid는
s = ( (-2 -0 + (-1-j) +(-1+j) ) - 0 )/4 = -3
각도는 (180+360*k)/(4-0) = 45도, 135도, 225도, 315도 이다.
Branch 4개의 Zero에서 출발했다가 S = -3에서 4개의 infinity Zero로 뻗어나가며,
System Characteristic Equation은 S = -3에서 4개의 중근을 갖게된다.
위의 두 예시에서의 Break out Point는 모두, Asymptote의 Centroid와 같은지점이었다.
그렇다면, Break out Point는 Asymptote의 Centroid와 같은 지점에서 출발할까?
->아니다.
Break in, Break out 포인트는 Asymptote의 Centroid와 다르다.
이 예시에서 두개가 우연히 같았던 것이다
두개념을 혼동하지 않도록 주의하자.
지금부터 살펴볼 예시를 통해,
Break Out과 Break in Point의 위치를 정하는 방법에대해 알아보도록 하자.
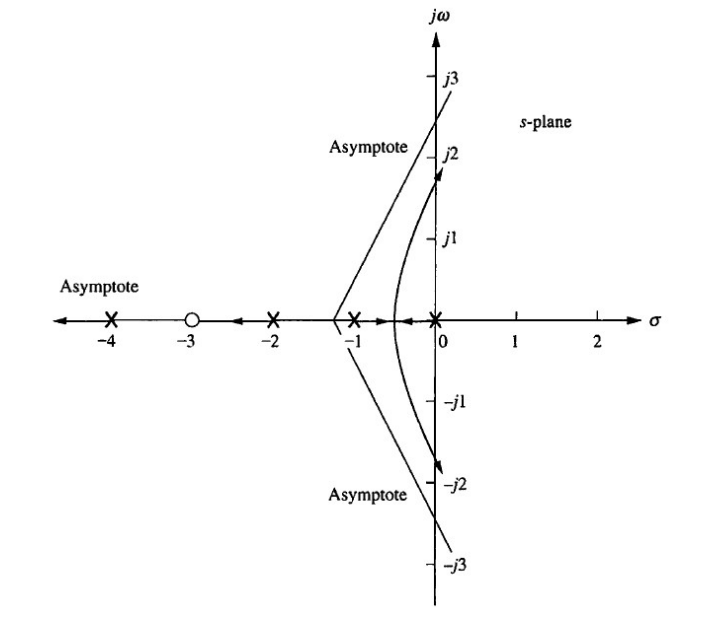
만약 아래와같은 Root Locus가 있다고 할때

Break in, Break out을 어떻게 판단해야 할까?
우선, 그림을 봤을때,
2개의 Pole, 2개의 finite Zero가 존재하므로,
infinite Zero는 존재하지 않고, Asymptote역시 존재하지 않는다.
그리고 2개의 Branch가 2개의 Pole에서 출발해 2개의 Zero를 향해 이동하는데,
Pole과 Pole사이 한 지점에서 Break out,
Zero와 Zero사이 한 지점에서 Break in Point가 존재한다.
-> 앞서봤던 예시와 다르게 여기서는 Asymptote가 존재하지 않으므로 Centroid도 존재하지 않는다.
어떻게 Break in, Break out 지점을 판단할까?
결론부터 이야기하면 아래와 같다.

*아래의 그래프는 Branch가 Real Axis위에 있을때를 따진것이고,
Branch가 Real Axis 위에 없다고해서 K값이 증가하지 않는것은 아니다. -> Zero로 향함에 따라 K는 계속 증가하고 있다.
그리고 여기서, 아래의 K값의 그래프를 보면 알겠지만,
K의 기울기 변화가 0이 되는 지점, 즉,
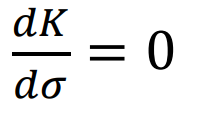
이 되는 지점이 바로 Break out, Break in Point가 된다.
이에 대한 증명은 아래와 같다. (증명은 항상 그랬듯... 보고 응 그렇구나 하면된다)
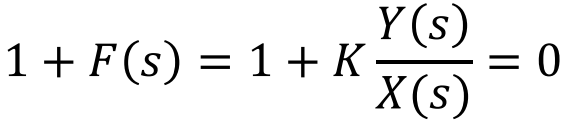
여기서 Characteristic Equation은
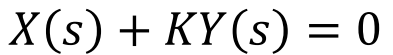
여기서, K가 Break out, Break in Point가 될 때라고 가정하고
아주 미세하게 K를 아래와 같이 옮기면,
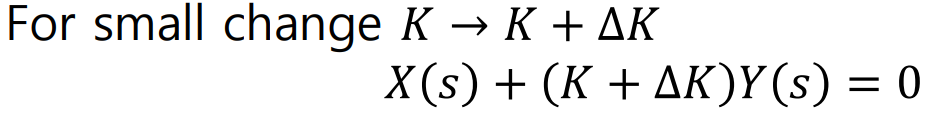
이것을 원래의 Characteristic Equation으로 나누면
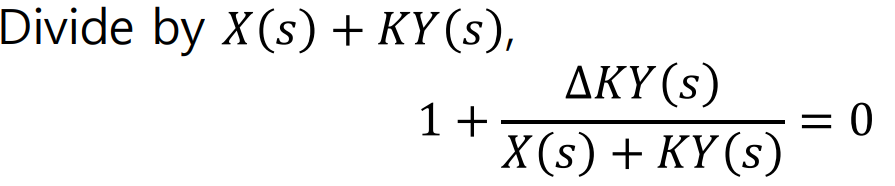
여기서, 재밌는 부분은, 위의 식의 분모인 X(s) + K*Y(s)는 원래의 System의 Characteristic Equation으로,
이때 Break in 또는 Out Point로서 Repeated Pole임을 가정하면,
아래와같이 쓸 수 있다.
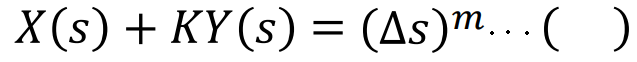

즉, 아래의 관계가 성립되므로,

Break in, out의 point를 정할 수 있게된다.
아래 예시를 통해 알아보자
Example1)
좀전에 그림으로 봤던 예시이다
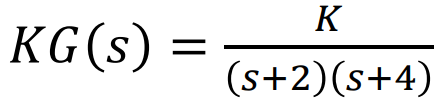
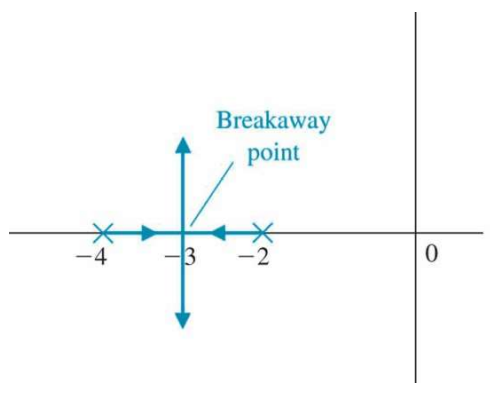
여기서 Characteristic Equation은

이고, K에 대한 식으로 바꿔주면

이를 실수 σ 에 대해 미분해주면

이므로, Break Away Point는 s = -3이 된다.
조금더 복잡한 아래 예시를 보도록 하자.
example2)

일 때, 위의 과정을 그대로 거쳐보자.
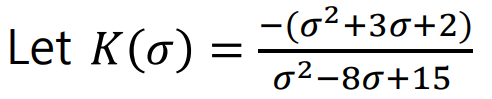
에서,

여기서 구한 각 값이 Break Out, Break in Point가 되며, 이를 그림으로 표현하면
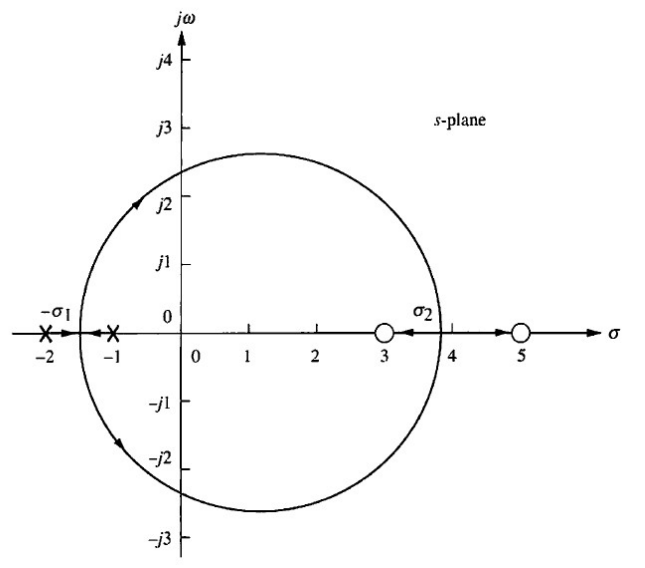
마지막으로 조금더 복잡한 예시를 살펴보고 Step 5를 마무리해보자.
Example3)
이번 예시에서는 Break Point뿐 아니라
Asymptote까지 한번 살펴보도록 해보자.

위와같은 Closed Loop Feedback System이 있다고 할때,
Characteristic Equation은

Pole의 개수 3개, finite Zero의 개수가 1개, 즉,
Asymptote개수는 2개이며, 각도와 Centroid는

이제 Break Point를 살펴보자.
Characteristic Equation에서 K에 대한 식으로 표현하면

이를 미분해보면
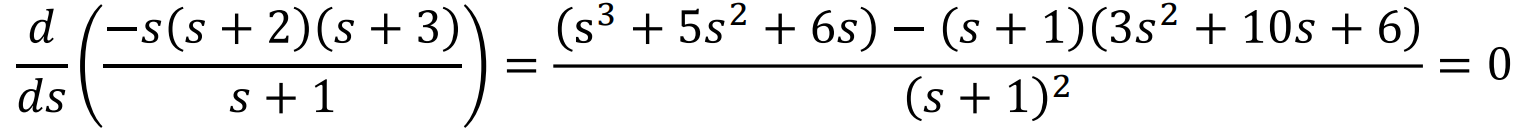
분자만 살펴보면

에서,
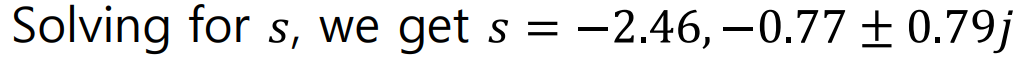
이다.
이 예제에서, Pole과 Zero가 모두 Real Axis Line위에 놓여있으므로,
break Point역시 실수축 위에 놓이므로, 위의 계산결과에서 나온 Complex number는 무시해도 된다.
즉, Break Point는 s= -2.46이 되며, Pole로부터 출발하므로 Break Out Point가 된다.
이를 Graphical하게 표현하면
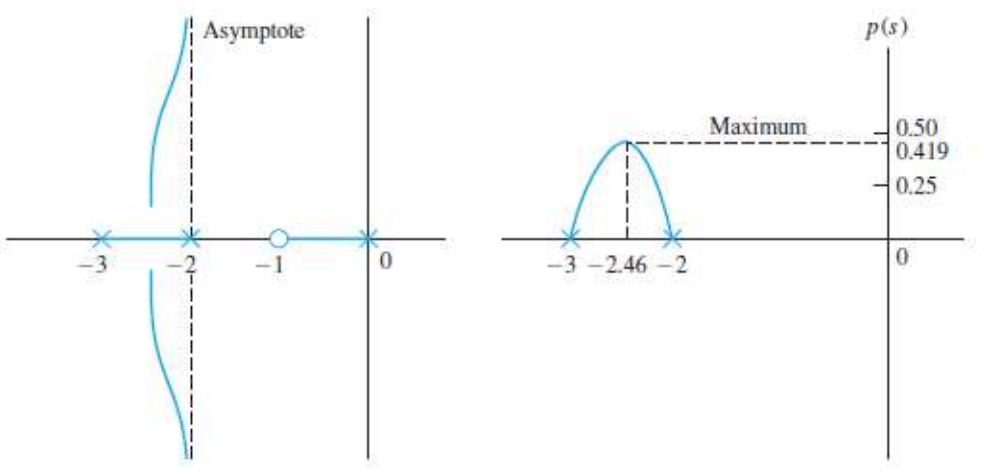
○ Step 6: Root Locue(Branch)의 출발 각도
앞선 예제들에서는, Pole과 Zero가 모두 Real Axis line위에 놓인 경우만 봤기 때문에,
Root Locus의 출발 각도는 항상 Real Axis Line과 일치하는 0도였다.
만일 Pole과 Zero가 Real Axis위에 놓여있지 않다면 어떻게 해석해야 할까?
먼저 출발지점부터 생각해보자.
여기서도 변함없이 Root Locus는 K값의 변화에 따라 Pole에서부터 출발하여 Zero로 뻗어나가기 때문에
마찬가지로 Pole이 출발지점이 되고, Finite Zero, 또는 infinite Zero를 향해 Pole이 이동한다.
Angle Condition을 만족한채로 말이다.
위쪽에서 따졌던 Phasor 180도 조건을 잊지말자.
여기서, 이 Angle Condition을 이용해서,
Pole에서 출발한 시점에서의 Root Locus의 각도를 구할 수 있는데,
해당 Pole에서의 출발지점과 해당 Pole의 위치가 크게 차이나지 않기 때문이다.
무슨말이냐 하면,
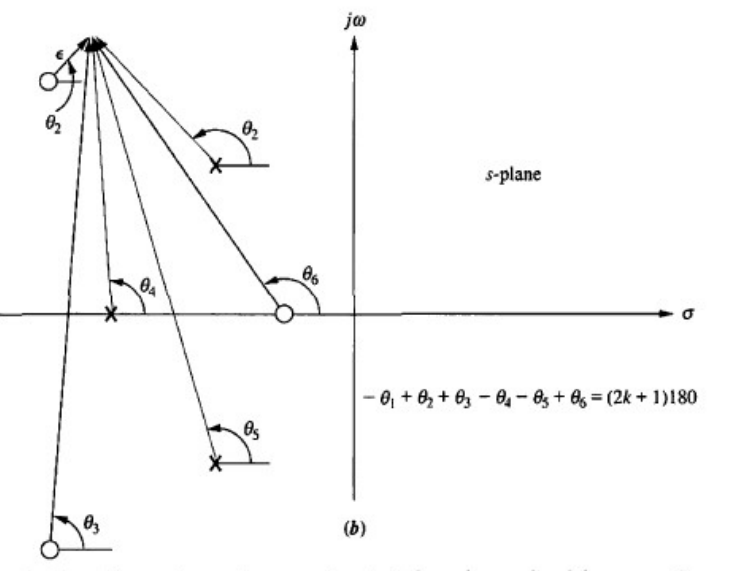
아래 그림을 살펴보자.

만일 우리가 구하고자 하는 Root Locus가 P1에서의 Root Locus라고 하고,
이때의 출발각을 Theta1이라고 해보자.
여기서, P1을 떠나 막 출발한 지점을 ε라고 하면
원래는 ε과 각 Pole이 이루는 각도로 Angle Condition(180도 Phasor조건)을 따져줘야 하지만,
막 출발한 상태에서(출발각을 구하는 상태에서)는,
ε과 P가 큰차이가 없다고 볼 수 있기 때문에 아래처럼 각 Pole의 위치로만 Angle Condition을 적용해도
이를 Approximation관점에서 해석할 수 있게된다.

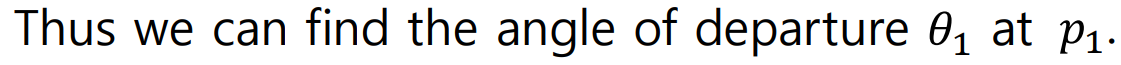
다른 Pole에서의 출발각을 구할때도 위와 마찬가지로 구해주면 된다.
Step 6도 간단한 예시로 이를 이해해보도록 하자.
Example)
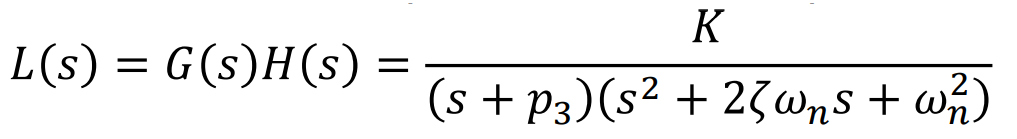
여기서 3개의 Pole이 있는데 하나는 s = -p3 이고 나머지 두개는
Underdamping상황이라고 했을때 두개의 Complex Root (Pole)이라고 해보자.
이를 그림으로 표현해보면
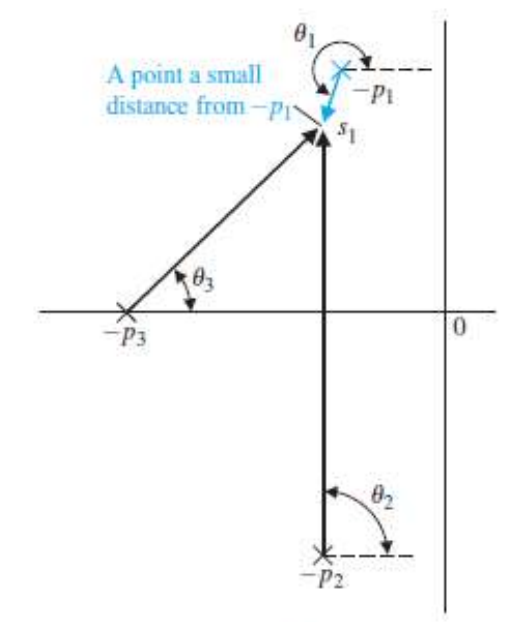
이 시스템은 Pole의 개수는 3개이고, Zero는 없기 때문에,
3개의 infinite Zero를 향해 Root Locus는 이동하고, Asymptote는 3개이다.
여기서, 각 Pole의 출발각을 구하려면, 아래처럼 간단하게 구할 수 있다.
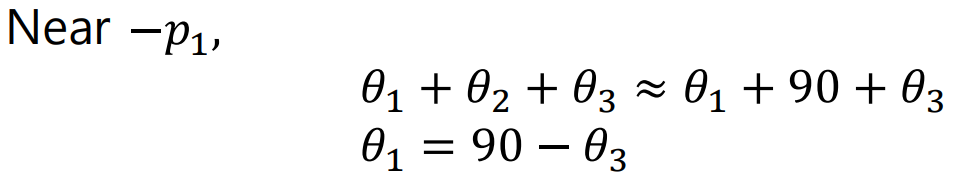
○ Step 7: Complete Sketch
Root Locus를 그리기위한 인피니티 스톤이 드디어 다 모였다....
지금까지의 6가지의 Step을 죽 살펴보면
○ Step 1 : Write the Characteristic Equation
○ Step 2: Real Axis 위에 놓인 Pole 판단
○ Step 3: Loci가 따라가는 점근선(Asymptote) : to infinity Zero
○ Step 4 : Locus가 imaginary Axis위를 지나는지 판단 (by Routh–Hurwitz criterion)
○ Step 5: Real Axis에서, Break away Point와 Break In Point 구분
○ Step 6: Root Locue(Branch)의 출발 각도
이 6가지 과정을 모두 참조해서 Root Locus를 (대강)그려주면 된다.

Step1~6에대한 예시로 이번 포스팅을 마무리해보겠다.
한번 쭉 따라가보는걸 추천한다..(글쓰는데 너무 오래걸려서...추후에 시간있으면 정리해놓도록 하겠다..)
위에서 다 다룬것들이라 크게 어렵진 않을거다(아마)




여기서, 우리가 찾고자하는 시스템이 존재한다고 하면, 어떻게 Parameter를 찾을까?
앞선 포스팅에서 System의 Performance에대한 index, Tp, Ts, P.O등을 다루면서
S-Plane상에 이것들이 어떻게 표현되는지 살펴보았다.
여기서 마찬가지로 적용해주고, 앞선 과정을통해 그린 Root Locus와 교점을 찾아주면 된다.
아래의 예시를 통해 이를 이해해보자.

....내용이 많기도하고 어렵기도 해서 유난히 힘들었던 포스팅이었다.
다음 포스팅에서는
조금더 심화된 Root Locus내용을 다뤄보도록 하겠다.
'Control > 자동제어' 카테고리의 다른 글
| Frequency Response Method - polar plot (0) | 2021.12.28 |
|---|---|
| The Root Locus(1) (0) | 2021.12.03 |
| The Stability of Linear Feedback System (0) | 2021.11.23 |
| The Performance of Feedback Control Systems (2) (0) | 2021.11.13 |
| The Performance of Feedback Control Systems (1) (0) | 2021.11.12 |




