정리노트
Deep Deterministic Policy Gradient (DDPG) 본문
Deep Deterministic Policy Gradient는
- DQN: https://arxiv.org/abs/1312.5602
- Deterministic Policy Gradient https://proceedings.mlr.press/v32/silver14.html
두가지를 합친 알고리즘입니다.
DDPG는 기존 DQN이 풀지못했던
"연속적인 Action Space에 대한 Policy 최적화"를
Deterministic Policy Gradient 도입하여 효과적으로 해결하였으며,
2016 ICLR (International Conference on Learning Representations)에
"continuous control with deep reinforcement learning"
https://arxiv.org/pdf/1509.02971
라는 이름의 논문으로 처음 발표되었습니다.
1. Continuous 한 Action Space에서 DQN의 한계?
DQN 알고리즘은
어떤 State input에 대해서 어떤 행동 a를 취했을때,
해당 state, action 쌍의 가치가 얼마나 되는지를 추산하는 Q 네트워크를 학습시켜서
state가 들어왔을때 가능한 모든 action pair중 가장 큰 q값을 가지는 행동을 greedy하게 선택합니다.
문제는,
Q Network가 취할 수 있는 Action은 출력 Node개수로 정의되므로
이것을 Continuous하게 설정할 수가 없다는 점입니다.
(Action Space자체가 선형적 관계로 되어 Regression문제로 바꿀 수 있는 특이한 케이스 제외)
DDPG는 그렇기 때문에 Actor Critic 포맷을 사용하며
별도의 Policy Network (Actor)를 통해
Continuous한 Action Space에서도 잘 동작하도록 설계하였습니다.
2. Deterministic Policy (Actor) in DDPG
DDPG의 큰 특징중 하나는
이 Policy Network가 바로 Deterministic하다는 점입니다.
반대개념으로는 Stochastic Policy를 들 수 있는데,
Stochastic하게 접근하지 않고, Deterministic하게 접근하는 방식에 여러가지 이점이 있기 때문입니다.
어떤 환경 E에 대해서, State, Action 쌍에 대한 가치함수값은

위와같이 정의될 수 있습니다.
여기서 Next State에 대한것은 '환경'이 결정해주는것 까지는 문제가 없는데,
뒤에 gamma*E[Q(s`,a`)]의 텀은
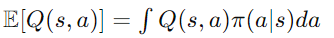
위 식처럼 policy에의해 결정된
action probability에 대한 각각의 q값을 적분해야만 계산이 가능한데 (action space가 continuous하기때문에)
이는 계산적으로 매우 복잡하고 비효율적이게 됩니다.
만약 해당 State에 대해서 Action을 토해내는
Policy Network (Actor)의 출력값을 Deterministic하게 결정하게 되면위같은 문제를 쉽게 해결할 수 있는데,
만약 Policy Network를 μ라고 하면,

기대값을 구하기위해 복잡한 연산을 하는게 아니라, 현재의 Policy Network가 선택한 action을 그대로 deterministic하게 선택해서 Q를 추산하면됩니다.
이렇게 할 경우에는 현재 Policy의 Action에대한 Probability를 고려하지 않아도 되고,
오직 '환경'에대한 영향만을 고려하여 Q(s,a)를 추산할 수 있기때문에, 계산복잡도도 훨씬 낮아지고,
무엇보다
'Q 값을 학습할 시에 Off-Policy 방식으로 학습이 가능'해진다는 장점도 생기게 됩니다. (오직 환경만이 영향을 미치므로)
2. How to get Gradients of Deterministic Policy?
위에서 정리한 내용을 아래 Policy Gradient의 목적함수에 대입해서 생각해봅시다.
Action Space가 Continuous할때,
Stochastic Policy에 대해서 목적함수 J(θ)는
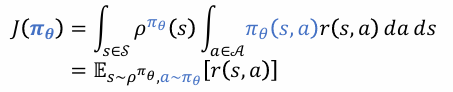
모든 Action Space에 대한 기대 보상의 합에 평균을 구해야하지만,
위에서 정리한대로 Deterministic Policy를 사용할 경우,
한방에 Q(지금 식의 notation에서는 r)를 추산하여 J(θ)를 쉽게 계산할 수 있게됩니다.

이를 Maximiazaition하기 위한 Gradient를 계산해야하는데,
식을 한번 정리해보면

이때, Policy μ는 θ에 대한 편미분과
Q(s,a)역시 행동 a에 대한 편미분은
둘다 계산하기 쉬워서, 간단하게 위 Gradient를 계산할 수 있습니다
+ 실제 구현시 Trck

Pytorch에서.... Gradient를 계산할때 θ에 대한 μ 편미분, 행동 a에 대한 Q(s,a) 편미분을 따로따로 계산할 필요없이 그냥

따로따로 구할필요없이 그냥 Q를 θ에대해 편미분 해주면 됩니다..
3. Ornstein - Uhlenbeck Process
Deterministic Policy를 선택했을때는
Q를 오직 '환경에서 얻어낸 정보'만을 가지고 추산할 수 있게 됨으로서,
Off-Policy 방식으로 Policy를 업데이트 하는 것이 가능하다고 정리하였습니다.
다만,이러한 Deterministic한 방식의 가장 큰 문제점은
바로 'Exploration'이 어렵다는 점입니다.
DDPG에서는 이를 보완하기위해 Ornstein-Uhlenbeck Process를 통해 행동정책을 결정합니다.
(다만,이것의 효용성에 대해서는 완전히 검증된것이 아니라고 합니다. 그래서 여기서는 간단하게 정리만 하고 넘기겠습니다)
DDPG에서 행동결정시 Exploration을 하기 위해 random variable ε 를 추가하게 되는데,
(ε = 0이면 Exlptation만 하는것)

이 ε 을 결정할때, 그저 어떤 uniform distribution을 가진 Random Variable을 추가해서 행동을 결정하는것은..
Controller성능에 부하를 매우 많이 주는것으로 알려져있어서,
DDPG에서는
random 확률변수를 선택하는것이 아니라, 어떤 '시간적으로 연관된 확률변수를 생성'하도록 합니다.
그리고 이것을 바로 Ornstein - Uhlenbeck Process라고 합니다.
-------
정리
DDPG는 Actor Critic포맷을 쓰는 Off-Policy 계열의 알고리즘으로....
- Critic Loss :

- Actor Loss의 Gradient :

- 그리고 이때, 행동정책은

을 사용하며 ε 는 Ornstein-Uhlenbeck Process를 따르도록 합니다.
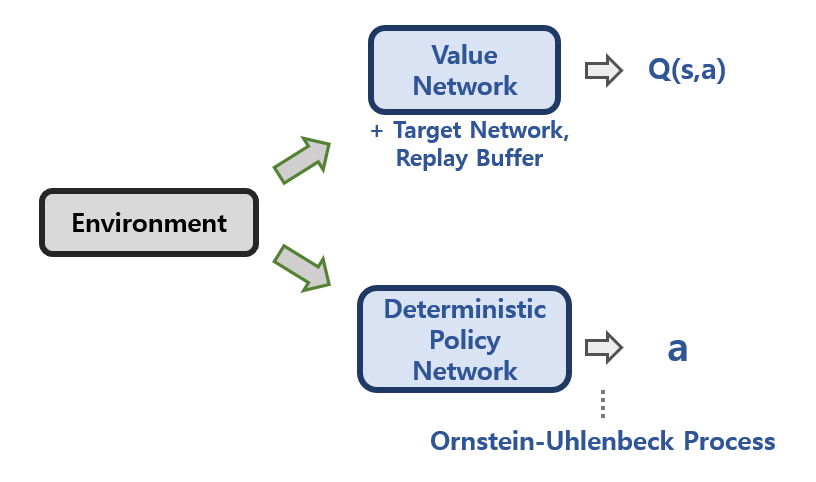
- 그리고 기존 DQN에 활용되던 기법인 Replay Buffer과 별도의 Target Network를 추가하여 학습합니다.
'AI > Reinforcement Learning' 카테고리의 다른 글
| Trajectory 최적화 관점에서 바라본 Policy Gradient (0) | 2024.05.20 |
|---|---|
| 단단한 강화학습 Chapter13_ 정책 경사도 방법(Policy Gradient Methods) (1) | 2023.05.16 |
| 단단한 강화학습 Chapter 9-11_함수근사(Function Approximation) (0) | 2023.05.08 |
| 단단한 강화학습 Chapter6_시간차 학습(Temporal-Difference Learning) (1) | 2023.04.21 |
| 단단한 강화학습 Chapter5_몬테 카를로 방법 (Monte Carlo Methods) (0) | 2023.04.11 |




