정리노트
단단한 강화학습 Chapter 9-11_함수근사(Function Approximation) 본문
단단한 강화학습 Chapter 9-11_함수근사(Function Approximation)
Krex_Kim 2023. 5. 8. 17:01이제 책의 1부에서는 Tabular 형식의 알고리즘을 다루었습니다.
이는 상태(State)와 행동(Action)에 대한 정의가 이산적인 표 형태라는 것을 의미합니다.
당연하게도 이러한 Tabular 형식은 한계가 있습니다.
가장 치명적인 단점은 행동 공간이나 상태 공간의 크기가 매우 크거나 무한한 경우(Contious한 Value일 경우),
학습이 불가능해진다는 점입니다.
2부에서 다루는 알고리즘은 이러한 문제를 함수 근사(Function Approximation)를 통해 해결하게 됩니다.
조금 더 구체적으로 말하면, GPI(Generalized Policy Iteration)에서 다루는 Value Function과 Policy에 대해 각각 함수 근사를 적용함으로써 연속적인 상황에서도 문제없이 가치와 행동을 결정할 수 있게 됩니다.
(최근에는 이러한 근사법 중 상당 부분이 딥 러닝(Deep Learning)을 통해 해결되어 많은 성능 개선이 이루어졌습니다.)
물론 함수근사 방식도 수렴성에 대한 보장을 잃는다는(그동안 수렴성에대한 수학적 정리는 따로 포스팅하지 않았지만) 단점이 있지만, 현실적인 문제에서 실제로 적용했을때 매우 좋은 성능을 보이고 있습니다.
이번 포스팅에서는 책의 2부에서 다루는 함수 근사 내용 중, Value Function의 근사에 대한 내용을 살펴보려고 합니다. 정책(Policy)의 경우, 정책 경사(Policy Gradient)라는 이름으로 Chapter 13에서 다루고 있습니다.
책의 2부가.. 조금 Classical한 내용이 너무 방대하게 기술된 것으로 느껴져서,
현재 개인적으로 듣고 있는 강의 내용 중 해당하는 내용들만 추려서 정리하려고 합니다.
◆목차
◎ 가치함수 근사 (Value Function Approximation)
◎ 예측목적(VE) (The Prediction Objective (VE))
◎ 확률론적 경사도와 준경사도 방법 (Stochastic Gradient and Semi-Gradient Methods)
◎ 선형방법 (Linear Methods)
◎ 비선형 함수근사 (Nonlinear Function Approximation: Artificial Neural Network)
◎ 최소제곱 TD (Least-Squares TD)
◎ 가치함수 근사 (Value Function Approximation)
책 2부 내용의 핵심은 바로 근사(Approximation)입니다.
이전 포스팅까지 다룬 내용이 Tabular한 형식으로 컴퓨터 메모리에 각 State와 Action에 해당하는 가치 값을 일일이 업데이트 해주는 방식이었다면,
함수근사에서는 어떠한 형태의 근사를 사용하더라도 이러한 State와 Action에 대한 Value함수를 추산하는 함수근사를 적용하여 상태와 행동공간이 연속적인(Continous) 무한한 경우에도 학습이 진행될 수 있도록 합니다.
가치함수 근사의 종류는 아래와같습니다
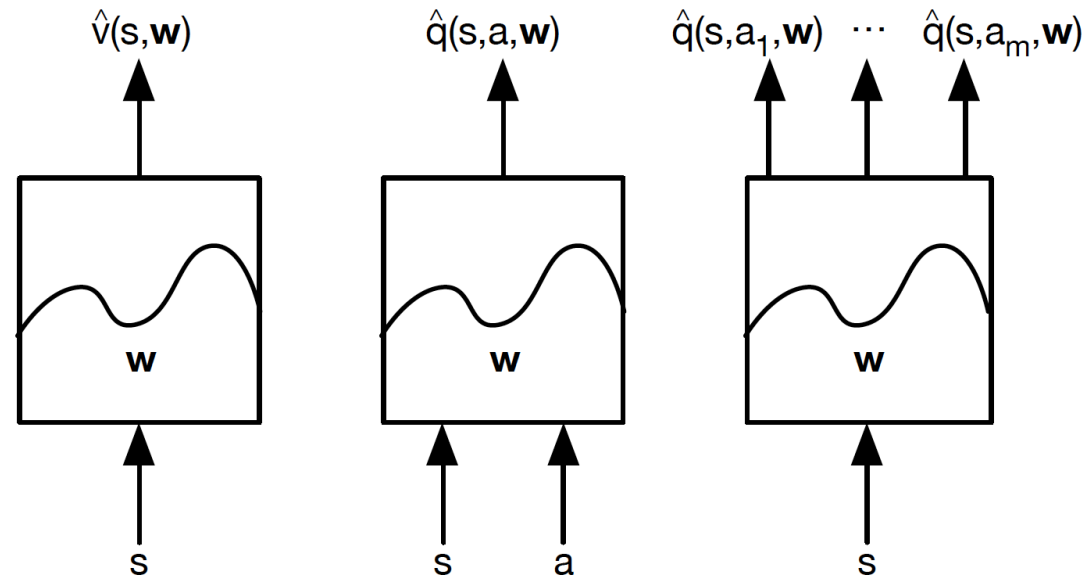
이러한 함수근사는 다양한 지도학습 기법과 푸리에기저를 통해서 진행될 수 있고, 책에도 잘 소개되어있지만,
근래에는 잘 쓰이지 않는 Classical한 방법이라 판단이들어서 스킵하고,
Deep Neural Network를 통해 가치값을 추산하는 방법을 중심으로 포스팅을 진행해보도록 하겠습니다.
◎ 예측목적(VE) (The Prediction Objective (VE))
가치함수를 추산할때, 으레 지도학습이 그렇듯 Loss 값을 줄이는 방향으로 Gradient Descent를 진행합니다.
이때 Loss값에 해당하는 부분을 아래와 같이 MSE를 통해 표현합니다.

책에따라서는 VE대신 J라는 Notation을 사용하기도 합니다.
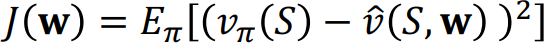
◎ 확률론적 경사도와 준경사도 방법 (Stochastic Gradient and Semi-Gradient Methods)
딥러닝을 한번이라도 다뤄본 사람이라면 익숙하게 접할수 있는 개념인 Gradient Descent,
그중 Stochastic Gradient Descent(SGD)는 샘플 한개에 대해 Update를 진행하는 알고리즘으로서,
만약 Feature Vector n개와 Layer 한개에 대한 가치값 추산이라고할때, Loss가 위에서 정의한 MSE 값이라면,
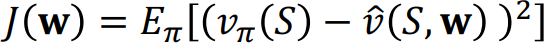


Gradient "Descent"과정이므로 가중치의 이동방향은 - 가 됩니다.
즉, Weight의 Update식은
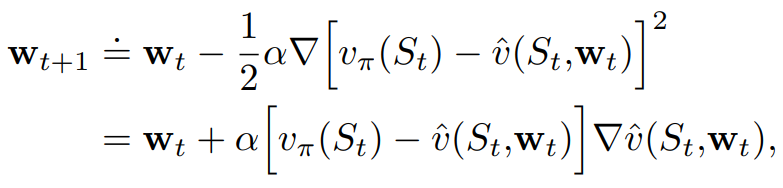
위 식을 보면, 결국 Vπ(St)라는 True Labeling값을 학습하는
v̂(St , wt)네트워크에 대한 학습이 됩니다.
여기서, 한가지 짚고 넘어가야할 점은, Vπ(St)를 바로 알 수 는 없으므로, 이 또한 추산하고있는 값이라는 점입니다.
즉, Vπ(St)를 실제 Real True값이라고 하고 이 값이 추산되고있는 중간 값 무언가를 Ut라고 하면

이때 Ut를 정할때, 방식에 따라 아래와 같이 생각해볼 수 있습니다.
Monte Carlo를 통해 추산한다고 하면,
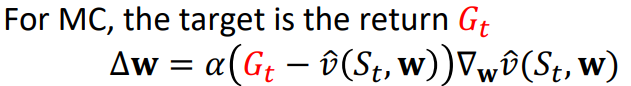
TD(0)방식이라면,
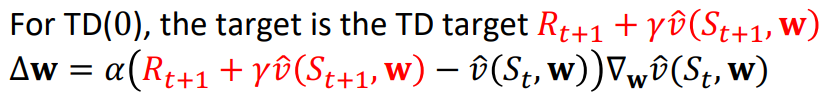
TD(λ)방식이라면,

만약 State Value 가 아닌, Action Value Function일경우에도 마찬가지로 적용할 수 있는데,
이때는 J(w)가 아래와같이 정리되며,

ΔW값을

로 쓸 수 있으며,
이 qπ(S,A)를 무엇으로 추산하는지에 따라

위와같이 정리할 수 있습니다.
(그리고,이때 Q에 대한 TD는 SARSA라고 불립니다)
+
일반적으로, 가치함수를 추산할때,
부트스트랩(bootstrapping) 방식을 사용할 경우 편향(bias)이 있는 추정이라고 생각할 수 있습니다.
만약 Ut를 추산할때, 이러한 편향이 없는 추정을 진행한다면, Wt가 Local Minimum으로 수렴한다는 것이 보장됩니다.
그러나 편향이 있는 추정을 한다면, 즉, Bootstrapping 방식이 사용된 Gradient Descent라면, 진정한 의미의 Gradient Descent라고 하기가 힘들어지는데, 이유는 Ut값 자체가 실제값과는 다른 편향된 값을 띄게 될 것이기 때문입니다.
그러나, Linear Approximation이 적용된 경우에 대해서는
Bootstrapping이 적용된 방법 역시 안정적인 수렴성을 보장받을 수있고, Global Minimum에 수렴하게 됩니다.
조금더 정리해보자면,
Bootstrapping이 적용되지 않은, 즉, 편향되지않은 Return Gt에 따라 Ut를 추산할 경우,
실제 Vπ와 같지만 Noise가 심하게되고, 이에 따라 Local Minimum에 수렴합니다.


그러나 Bootstrapping이 적용된, 즉, 편향된 Rt+1 + γv̂(St+1,w)에 따라 Ut를 추산할 경우,
실제 Vπ와는 조금 차이가 생기지만 Noise에 강하게 되고 (TD가 Noise에 강한것 처럼) 만약
Linear Appriximation이 적용된 Bootstsrapping에 한해서는 Global Minimum에 '이론적으로' 수렴이 보장됩니다.
(증명은 책에 있으나 따로 다루지는 않겠습니다)


여기서 이론적이라고 굳이 표현한 이유는,DQN같은 알고리즘은 Linear Approximation이 아닌, Deep Neural Network를 쌓은 Non-Linear Approximation이 적용된 TD계열의 Q-Learning인데, 그럼에도 불구하고 현실적인 문제에서 잘 학습이 진행됩니다..실제 현실에서는 꼭 그렇지 않을 수도 있기 때문에 '이론적'이라고 표현했습니다.
◎ 선형방법 (Linear Methods)
Value Function에대한 Linear Approximation은,
다음과같이 표현해볼 수 있습니다.
State를 표현하는 Feature Vector n개에 대해서
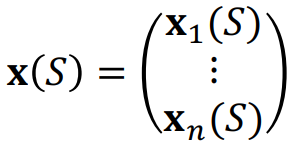
이에대한 Value Function 선형 근사는

즉, 위의 가치함수의 Weight Update식

은
만약 선형근사된 가치함수라면,
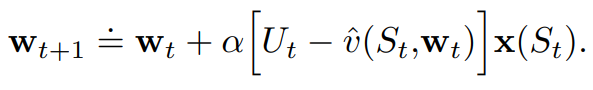
로 표현이 가능해집니다. (w*x(s)에서 w에대한 Partial Derivative는 x(s))
◎ 비선형 함수근사 (Nonlinear Function Approximation: Artificial Neural Network)
가치함수를 추산하는데 선형근사가 아닌, 비선형 근사를 이용할 수도 있습니다.
비선형 함수 근사를 이용한 강화학습에서 인공신경망 (Artificial Neural Network)이 중요한 역할을 합니다. 선형 근사 방법과 달리, 인공신경망은 복잡한 패턴이나 상호작용을 포착하는 데 뛰어난 성능을 발휘할 수 있습니다.
인공신경망은 여러 계층으로 구성되어 있으며, 각 계층은 선형 변환과 비선형 활성화 함수로 구성됩니다. 이러한 구조 덕분에 인공신경망은 다양한 형태의 복잡한 함수를 근사할 수 있습니다.

또한 인공신경망은 다양한 데이터 유형에 적용할 수 있습니다. 예를 들어, 이미지와 같은 고차원 데이터를 다룰 때는 Convolutional Neural Network (CNN)을 사용할 수 있습니다. CNN은 이미지의 지역적 패턴을 학습하는 데 효과적인 Convolutional Kernel을 활용하여 가치함수를 추정합니다.

◎ 최소제곱 TD (Least-Squares TD)
Least Square Prediction (LSP)방법은 하나의 Sample이 아니라 여러 Sample을 통해 가치하는 근사하는 Batch Method방법의 일종으로, 데이터셋 D의 모든 상태-가치 쌍에 대한 실제 가치 V와 근사 가치 v̂ 사이의 제곱 오차의 합을 최소화하는 것을 목표로 합니다.

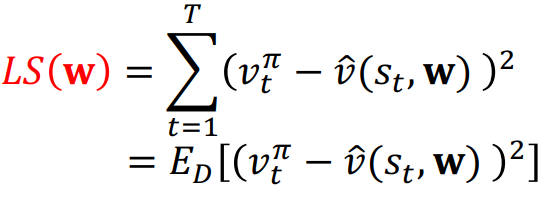
여기서 E_D는 데이터셋 D에 대한 기댓값을 의미하며,
v̂는 가중치 w와 상태에 대한 Feature Vector를 곱한 값입니다.

Least Square Method의 장점 중 하나는 데이터가 데이터셋 D 내에서 재활용될 수 있다는 점입니다. LSP는 전체 데이터셋 D에 대한 오차를 최소화하는 것이 목표이므로, 이미 사용한 상태-가치 쌍을 여러 번 사용해도 문제가 없습니다. 이를 통해 학습 과정에서 데이터의 효율성이 높아집니다. 이렇게 데이터의 재활용이 가능한 점은 강화학습에서의 가치 함수 근사에 있어 Least Square Method를 유용하게 만드는 요소 중 하나입니다.
(책에서, 선형 근사를 사용하는 LSP의 경우 셔먼-모리슨 공식을 적용하여 계산을 더 쉽고 효율적으로 할 수 있음을 보이는데, 이부분은 생략하도록 하겠습니다.)
+ 참고
Precition 알고리즘의 Convergence



'AI > Reinforcement Learning' 카테고리의 다른 글
| Trajectory 최적화 관점에서 바라본 Policy Gradient (0) | 2024.05.20 |
|---|---|
| 단단한 강화학습 Chapter13_ 정책 경사도 방법(Policy Gradient Methods) (1) | 2023.05.16 |
| 단단한 강화학습 Chapter6_시간차 학습(Temporal-Difference Learning) (1) | 2023.04.21 |
| 단단한 강화학습 Chapter5_몬테 카를로 방법 (Monte Carlo Methods) (0) | 2023.04.11 |
| 단단한 강화학습 Chapter4_동적 프로그래밍 (Dynamic Programming) (1) | 2022.11.02 |




