정리노트
Trajectory 최적화 관점에서 바라본 Policy Gradient 본문
https://roboharco12.tistory.com/62
단단한 강화학습 Chapter13_ 정책 경사도 방법(Policy Gradient Methods)
지금까지 포스팅에서 다뤘던 내용은, Value Based 방식으로, 가치함수를 통해 Policy를 결정하는 것들이었습니다.이번 챕터내용은 가치함수 없이도 행동을 선택할 수 있는 파라미터 기반의 정책(정
roboharco12.tistory.com
에서 정의했던것 처럼,
Policy Gradient의 목적함수는 Episodic Task상황에서
아래와 같이
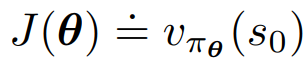
initial state로 정의 합니다.
Policy Gradient는 이 J(θ)를 Maximize하는것이 목표이며,
이것을 그냥 심플하게 말로 풀어쓰면 임의의 Initial State S0에서 향후 받게될 Reward를 Maximization하는 것과 같습니다.
보통 이 V를 추산하기위해서

☞ 어떤 State의 분포가 시간 t가 계속 흐르면 어떤 stationary distribution를 따르게 된다'는 가정과

☞ Gt 가치값을 Q, 또는 Advantage function을 이용해 추산할때 Bellman Equation을 이용한다는 가정
두가지 가정을 전제하였었는데,
여기서는 이 두가정을 잠시 생각하지 않고,
아래
Policy Gradient 목적함수의 Gradient 수식을
'Trajectory관점에서' 어떻게 바라볼 수 있는지 정리해보겠습니다.

결국 Policy Gradient에서의 학습 목적은
향후 Return값의 합을 높게 만들어줄 수 있는 Trajectory를 찾는 것입니다.


Trajectory를 τ로 표현할때

일때,
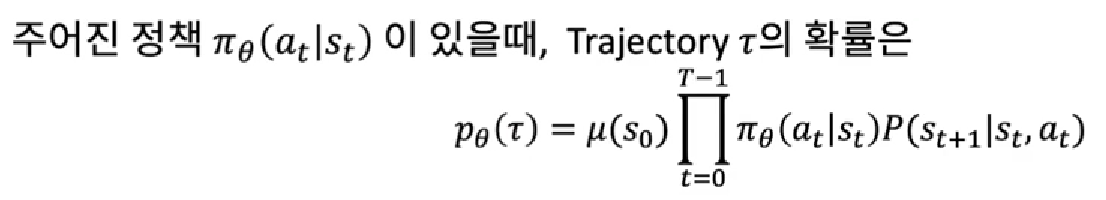
이 되고, log를 활용하여 정리해보면
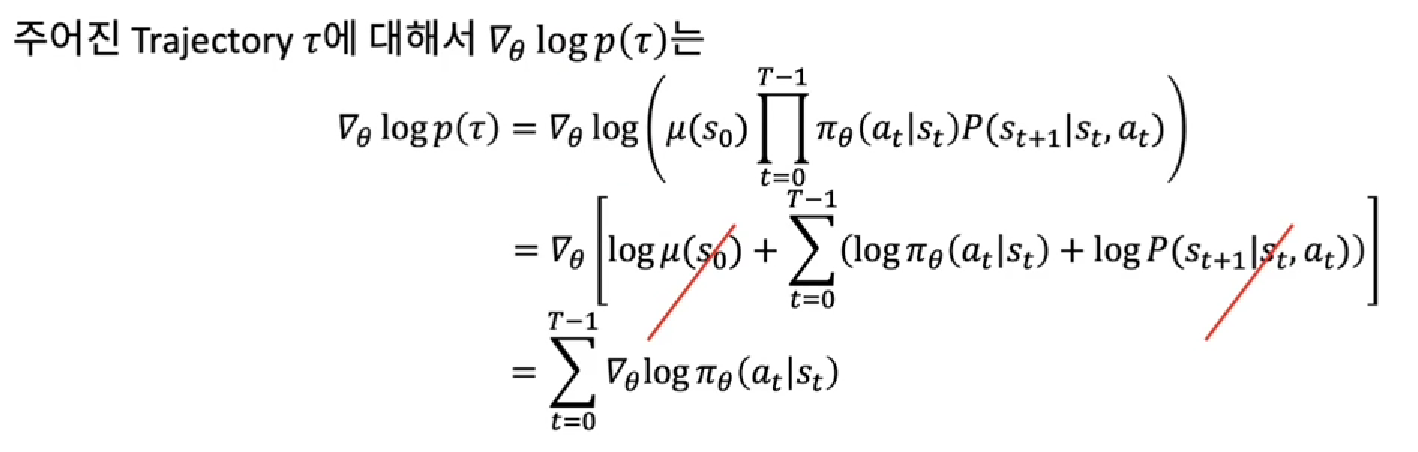
즉,
∇ log(P(θ))는 Σ∇log(𝝿(a|s))이고,
이는
'어떤 policy를 따를때, 해당 Trajectory가 나올 확률'
로 해석됩니다.
즉,
아래의 최대화 하고 싶은 J의 Gradient식으로 돌아왔을때

이를 다시 아래처럼 정리하였을때

위 빨간색이 의미하는 것이 바로
'어떤 policy를 따를때, 해당 Trajectory가 나올 확률'
가 됩니다.
R(τ)는 해당 Trajectory를 따랐을때 받는 Return의 합, 즉, Value값이고..
즉,
이사실을 근거하여 아래 Policy Gradient의 목적함수의 gradient를 다시 해석해보면

'AI > Reinforcement Learning' 카테고리의 다른 글
| Deep Deterministic Policy Gradient (DDPG) (0) | 2024.05.20 |
|---|---|
| 단단한 강화학습 Chapter13_ 정책 경사도 방법(Policy Gradient Methods) (1) | 2023.05.16 |
| 단단한 강화학습 Chapter 9-11_함수근사(Function Approximation) (0) | 2023.05.08 |
| 단단한 강화학습 Chapter6_시간차 학습(Temporal-Difference Learning) (1) | 2023.04.21 |
| 단단한 강화학습 Chapter5_몬테 카를로 방법 (Monte Carlo Methods) (0) | 2023.04.11 |




