정리노트
단단한 강화학습 Chapter13_ 정책 경사도 방법(Policy Gradient Methods) 본문
단단한 강화학습 Chapter13_ 정책 경사도 방법(Policy Gradient Methods)
Krex_Kim 2023. 5. 16. 23:34지금까지 포스팅에서 다뤘던 내용은, Value Based 방식으로, 가치함수를 통해 Policy를 결정하는 것들이었습니다.
이번 챕터내용은 가치함수 없이도 행동을 선택할 수 있는 파라미터 기반의 정책(정책에대한 근사)을 학습하는 방법에 대해 다뤄보겠습니다.
앞서 가치함수 근사에서는 w라는 Notation으로 실제 Value값과 일치하게 근사하도록 J(w)에 대한 Gradient Descent를 수행했다면,
이번 Policy Gradient에서는 Policy에대한 목적함수 J(θ)를 최대화하는 Gradient Ascent를 수행합니다.


Value Function와 Policy에 대해 동시에 학습하는 것을 Actor-Critic이라고 합니다.

이번 포스팅에서는 Actor Critic 모델로 넘어가기전, Policy Gradient에 대한 개념을 우선 중점적으로 다뤄보도록 하겠습니다.
◆목차
◎ 정책 근사 및 정책 근사의 장점 (Policy Approximation and its Advantages)
◎ 정책 경사도 정리 (The Policy Gradient Theorem)
◎ REINFORCE: 몬테카를로 정책 경사도 (REINFORCE: Monte Carlo Policy Gradient)
◎ 기준값이 있는 REINFORCE (REINFORCE with Baseline)
◎ 간단한 Baseline Trick: 리턴 표준화
◎ 행동자-비평자 방법 (Actor–Critic Methods)
◎ 연속적인 문제에 대한 정책 경사도 (Policy Gradient for Continuing Problems)
◎ 정책 근사 및 정책 근사의 장점 (Policy Approximation and its Advantages)
일반적인 Value Based 강화학습의 단점은,
행동공간의 크기 |A|가 커지면, 학습이 매우 힘들어지며, 연속적인 행동공간의 경우 학습이 난감하고, 또한
Policy를 정할때 대부분의 경우에서 Deterministic하게 (Not Probabilistic) 선택할 수 밖에 없다는 단점이 있습니다.
Policy를 가치가아닌, 데이터로부터 직접 학습하게 될 경우 이러한 단점을 효과적으로 극복할 수 있습니다.

이러한 Policy Gradient는 Policy를 아래와같이 Probabilistic하게 파라미터화 할 수 있는데, 이때
π(a|s, θ)가 θ에 대해 미분이 가능해야하며, s와 a는 유한한 값이어야 합니다.

여기서 h는 선호도 (preference)를 의미하며,

이러한 종류의 정책 파라미터화 방법을 행동 선호도에서의 소프트맥스 (Soft-max in action preference)라고 합니다.
◎ 정책 경사도 정리 (The Policy Gradient Theorem)
Policy Gradient는 상황에 맞는 목적함수가 존재하는데, 보통 Episodic Task에는 아래와 같은 목적함수를 가집니다.

Episodic Task의 경우 목적함수를 Start Value인 s0에 대한 가치함수로 정의합니다.
즉, 이를 maximize하는 θ에 대해 Gradient Update를 수행하기위해 아래와 같이 유도해 볼 수 있습니다.

모든 state에 대해서 미분은 위와같고,
이제 J(θ)를 구하기 위해 s0에 대해 이를 대입해주면

결과 부분만 추려서 보면 아래와 같습니다.

◎ REINFORCE: 몬테카를로 정책 경사도 (REINFORCE: Monte Carlo Policy Gradient)

위의 결과부분을 조금더 구체화시켜본다면

이 되며, 이는 곧

이 됩니다.
결론만 보면

이 됩니다.
즉, 목적함수 J(θ)에 대해 Maximize하는 아래의 Gradient Ascent

를 수행하기 위해서는 Qπ(s,a)를 추산해야하는데,
이때 Monte Carlo 방식으로 추산한 알고리즘을 REINFORCE 알고리즘이라고 합니다.



◎ 기준값이 있는 REINFORCE (REINFORCE with Baseline)
REINFORCE 알고리즘은 한마디로, "MC 방식의 Policy Gradient"라고 할 수 있습니다.
그런데 이런 MC 기법들의 고질적인 문제는 바로 Variance가 높아 Outlier에 취약하다는 점이었습니다.

그리고 Q Value를 MC로 추산하는 REINFORCE 역시 이러한 분산문제에서 자유롭지 못합니다.
이를 해결하기 위해 나온 개념이 바로 Baseline입니다.

Qπ(s,a)에 Baseline이되는 어떠한 함수 b(s)를 빼주는 형태인데,
이때 b(s) Function은 행동 a에 대해 독립적인 함수라면 무엇이든 가능합니다.
이유는 아래와 같습니다.

즉, 행동 a와 독립이라면 뺄셈이 되는 부분에 해당하는 값이 결국 0이기 때문입니다.

기준값을 선택하는 자연스러운 방법중 하나는 상태가치의 추정값 v̂(s,w)을 기준값으로 선택하는 것입니다.
(다음 섹션에 다루겠지만, v̂(s,w)를 Bootstrapping방식으로 추산한다면, Actor Critic 모델이 됩니다)
이를 Advantage Function A(s,a)라고도 하는데,

이에 대해 Pseudo Code는 아래와같이 표현됩니다.


◎ 간단한 Baseline Trick: 리턴 표준화
Policy Gradient에서 Q를 추산할때, 적절한 Baseline을 찾을 수 있다면, 꼭 시도해보는 것이 좋습니다.
리턴 표준화는 그중 가장 대표적이면서도 잘되는 Trick으로, 내용은 아래와같습니다.

라고 했을때,

리턴의 평균과 표준편차를 이용하여 Gt를 아래와같이 추산하는 알고리즘입니다.


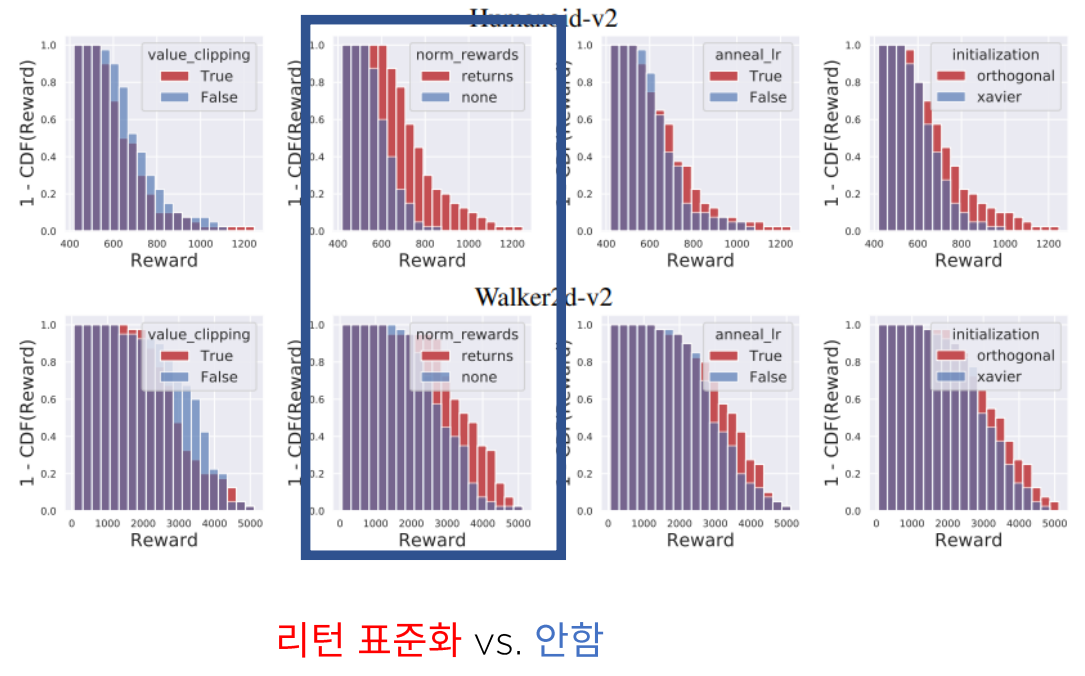
리턴 표준화는 생각보다 엄청 잘되는 Trick이라고 합니다.
<PPO로 잘 알려진 Proximal Policy Gradient>
https://arxiv.org/abs/1707.06347
Proximal Policy Optimization Algorithms
We propose a new family of policy gradient methods for reinforcement learning, which alternate between sampling data through interaction with the environment, and optimizing a "surrogate" objective function using stochastic gradient ascent. Whereas standar
arxiv.org
아래 ICLR 2019에 발표된 PPO에 대한 Case Study논문을 보면,
이러한 리턴표준화가 생각보다 중요하다는 것을 알 수 있습니다.
https://arxiv.org/abs/2005.12729
Implementation Matters in Deep Policy Gradients: A Case Study on PPO and TRPO
We study the roots of algorithmic progress in deep policy gradient algorithms through a case study on two popular algorithms: Proximal Policy Optimization (PPO) and Trust Region Policy Optimization (TRPO). Specifically, we investigate the consequences of "
arxiv.org
◎ 행동자-비평자 방법 (Actor–Critic Methods)
강화학습에서 매우 중요한 알고리즘 중 하나인 Actor-Critic 모델은 정책(Actor, 행동자)이 선택한 행동의 결과에 대해 피드백을 제공하는 방식으로 작동하는 알고리즘을 말합니다. 이 모델에서는 Actor가 행동을 결정하고, Critic은 그 행동의 결과로부터 학습을 통해 피드백을 제공합니다.
Actor-Critic 방법론은 반환값을 추정하기 위해 가치 함수 V값 (또는 Q-값) Bootstrapping하여 학습합니다.
(바닐라 버전은 V만 Boostrap인것으로 알고있습니다) Critic은 이러한 추정치를 통해 Actor의 행동 선택을 지도합니다.
이러한 Actor Critic 모델의 작동방식은 아래 그림과같은 비유로 설명될 수 있습니다.

REINFORCE에서 Policy Network를 학습할시, Q값을 Monte Carlo 방식을 통해 업데이트 했고,
이역시 Policy Network와 Q Value Function을 'Learning'하는 방식이지만, 책에서는 완전한 Critic 모델은 아니라고 설명합니다.
이해하기로는, 만약 baseline V(s)가 Bootstrapping이 아닌, MC처럼 Episode가 끝나야 추산할 수 있는 경우,
Advantage Function인 Q(s,a)-V(s)에서 한 Episode동안 V(s) baseline값은 고정이므로
이는 가치 추정값이 갱신되는동안 base line V(s)가 오직 '기준'값으로만 사용되기 때문에, 제대로 Critic 모델의 역할을 수행할 수 없다고 합니다.
한편, Q Value역시 Bootstrapping을 적용하여 추산하는것이 Monte Carlo 방식을 통해 추산할때 발생하는
분산 문제점을 해결할 수 있습니다.
아래는 One-Step Actor Critic 방식을 나타내는 식입니다.


정리하면,
Policy를 학습하기위해 Q(s,a)를 추산할때, MC 방식으로 추산하면 너무 분산이 커지니까, 이때 Baseline을 적용하는데
보통 이 Baseline은 V(s)를 사용하고,
이때 Q(s,a)와 V(s) 둘다 Bootstrapping방식을 주로 사용하며 이를 Actor Critic알고리즘이라고 합니다
◎ 연속적인 문제에 대한 정책 경사도 (Policy Gradient for Continuing Problems)
Continuing Task의 경우 목적함수 J(θ)를 조금 다르게 정의해주어야 합니다.
에피소드의 경계가 없으므로, 시간단계별 Reward 또는 가치함수값의 평균을 이용해 목적함수를 정의하는데,
평균 Value값인 경우,

평균 혹은 Time Step 마다의 평균 Reward 값인경우

그리고 이때 μ는 πθ(s)에 대한 Marcov chain의 Stationary Distribution으로

로 정의됩니다.

'AI > Reinforcement Learning' 카테고리의 다른 글
| Deep Deterministic Policy Gradient (DDPG) (0) | 2024.05.20 |
|---|---|
| Trajectory 최적화 관점에서 바라본 Policy Gradient (0) | 2024.05.20 |
| 단단한 강화학습 Chapter 9-11_함수근사(Function Approximation) (0) | 2023.05.08 |
| 단단한 강화학습 Chapter6_시간차 학습(Temporal-Difference Learning) (1) | 2023.04.21 |
| 단단한 강화학습 Chapter5_몬테 카를로 방법 (Monte Carlo Methods) (0) | 2023.04.11 |




