정리노트
단단한 강화학습 Chapter3_(2) _유한 마르코프 결정 과정(Finite Markov DecisionProcesses) 본문
단단한 강화학습 Chapter3_(2) _유한 마르코프 결정 과정(Finite Markov DecisionProcesses)
Krex_Kim 2022. 10. 9. 16:09지난번에 이어서 계속 포스팅 해보도록 하겠습니다.
◆목차
◎ 정책과 가치함수 (Policies and Value Functions)
◎ 최적 정책과 최적 가치 함수 (Optimal Policies and Optimal Value Functions)
◎ 정책과 가치함수 (Policies and Value Functions)
정책(Policy)과 Value function(가치함수)는 거의 모든 강화학습 알고리즘에 적용되는 개념입니다.
Value function(가치함수)이란, "Agent가 현재 주어진 State에 있을때, 혹은 어떤 Action을 취할때 이것이 얼마나 좋은가"의 정량적 수치를 추정하는 함수를 말하며,
여기서 "얼마나 좋은가?"를 자세히 말하면 "Expected Sum of Future Reward"를 의미하게 됩니다.
* 이전 DRL_Introduction 포스팅에서 'Expected', 'Sum', 'Future', 'Reward' 의미단위로 이를 자세히 풀어서 정리했습니다.
https://roboharco12.tistory.com/49
DRL_Introduction_(1) Marcov Decision Process_1
아래 영상은 곽동현 연구원님의 1시간 25분짜리 DRL 소개 영상인데요, Deep Reinforcement Learning에 대한 기본 틀을 잡고 시작하기 딱 좋은 영상이라 생각이들어서, 영상내용을 쭉 정리해보는 포스팅을
roboharco12.tistory.com
Agent가 미래에 받을 것으로 기대할 수 있는 보상(Expected Sum of Future Reward)은
현재 어떤 행동을 취할것인가에 달려있으므로,
Value Function은 행동을 어떻게 결정할지 정하는 Policy(정책)에 의해서 정의된다고 할 수 있습니다.
Policy(정책) π의 공식적인 의미는
State로부터 가능한 각각 행동에대한 선택 확률의 대응관계를 의미합니다.
예를들어, 에이전트가 시각 t에 Policy π를 따른 다면,
π를 아래와같이 확률로서 정의할 수 있습니다.

앞서 DRL_introduction포스팅에서 Value(가치)는
상태가치 (State Value)와 행동가치 (Action Value)두가지가 있다고 하였습니다.
Discounting Factor까지 고려하면,
각 Value를 아래와같이 간단하게 정리할 수 있습니다.
- State Value function for policy π

- Action Value function for policy π

Vπ와 qπ를 각각 정책 π에 대한 상태가치함수, 행동가치함수 라고 부릅니다.
강화학습에서
가치함수 Vπ와 qπ는 경험으로부터 추정하게 됩니다.
※ 참고
이 가치함수 추정 방식에 대해서 크게 두가지 관점으로 분류하여 정리할 수 있는데
바로 'Planning'관점과 'Learning'관점입니다.
Planning에서 기본이 되는 것이 바로 Dynamic Programming(DP)이며,
Learning에서 기본이 되는 개념은 Monte Carlo method(MC)입니다.
Dynamic Programming의 경우 모델에서 Model에서 특정행동을 했을때
어떤 결과가 도출될지 환경모델을 이미 알고있는 상태에서 진행하는 Model Based 추정 방식이며,
Monte Carlo방식의 경우, 특정 행동에 대한 결과가 불확실한 상황에서 진행하는 Model Free 추정방식을 의미합니다.
추후 이 두가지 방법이 합쳐져서 Temporal Difference Learning (TD Learning)이 됩니다
책에서 DP와 MC에 대해서 간단하게 정리만하고 넘어가고있어서 이부분에대해서 조금 더 언급해보고 넘어갔습니다.
Episode가 진행될때
Agent가 정책 π를 따르고,
여러번의 Episode에 대해서 모든 State와 Action들에 대한 각각의 평균 이득값으로 가치를 추정하는 방식을
Monte Carlo Method 라고 합니다.
이와 달리 Dynamic Programming에서는 평균이 아니라, 이미 환경모델에대해 정의된 p 함수를 이용하여 가치를 추정합니다. 그리고 이때 사용되는 가치추정 방정식이 바로 Bellman Equation입니다.

강화학습과 Dynamic Programming 전반에서 이용되는 Value Function은 위와같이
Recursive한 관계식으로 표현가능하다는 특성이 있습니다.
이를 아래 보강다이어그램을 통해서 조금더 자세히 살펴보도록 하겠습니다.

상태 s 가 두개의 다음 상태 s`와 맞닿아있고,
이때 Policy π를 통해 선택가능한 Action이 3가지가 있다고 하면,
각 Action이 선택될 확률은 π(a|s)에 의해 정의됩니다.
그리고 이때 각 Action을 취했을때 두가지의 s`중 어디로 가고, 어떤 reward를 받게될 지는 p(s`, r | s, a)에 의해 정의됩니다.
그 다음 상태 s`의 State Value인 Vπ(s`)를 알고,
환경모델을 통해 p(s`, r | s, a)에 대한 정보를 알고 있을 때 (Model Based),
현재 상태 s의 State Value를 추정하기위한 위의 Bellman Equation을 계산할 수 있게됩니다.
※ 상태와 행동의 가치에대한 보강 다이어그램을 비교하면 아래와 같습니다

◎ 최적 정책과 최적 가치 함수 (Optimal Policies and Optimal Value Functions)
앞서 강화학습 문제를 푼다는 것은 "Sum of Future Reward"를 최대한 많이 얻는 정책을 찾는 것을 의미한다고 정리하였고,
이에대한 기댓값인 Value를 어떻게 계산하는지 State Value와 Action Value 두가지 Value에 대해서 나눠서 정리해보았습니다.
이번 섹션은 이렇게 구한 Value를 가지고 가장 Optimal한 Policy를 어떻게 정의할것인가에 대한 내용을 다루고 있습니다.
책의 내용을 통해 이를 정의해보면,
º Value Function은 부분적으로 Policy들의 순위를 정한다.
º 모든 State에 대한 Value(Expected Sum of Rewards)가 정책 π1 에 비해서 π2가 더 크거나 같다면,
정책 π2가 π1보다 더 좋은 것으로 정의된다.
º 다시말해, 모든 s∈S 에대해 Vπ1(s)≥Vπ2(s)일 때만 π1(s)≥π2(s)라는 것이다.
º 다른 모든 정책보다 더 좋거나 아니면 같은 수준인 정책은 항상 하나이상 존재하고,
이를 최적정책 (Optimal Policy)라고한다.
º 두개 이상의 최적 정책이 있을 수 있으나, 모든 최적 정책을 π*(s)로 표기하고,
모든 π*(s)는 동일한 State Value Function와 Action Value Function을 갖는다.
º 이때 Optimal Policy가 갖는
State Value Function을 최적 상태 가치 함수 (Optimal State Value Function)이라하고,
Action Value Function을 최적 행동 가치 함수 (Optimal Action Value Function)이라 한다.
각각은 아래와같이 정의된다.

추가로, State - Action 쌍에대해 행동 a를 했을때 얻게되는 이득의 기대값이 q이고,
기대값을 Recursive하게 표현한다면
Optimal Action Value Function을 아래와같이 쓸 수도있다.
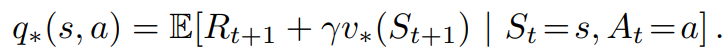
V*가 어떤 Policy에 대한 Value Function이고, 이것이 Bellman Equation을 따르게 된다면
Bellman Equation 고유의 특성인 Self Consistency(자기일관성)을 따라야 합니다.
하지만 Value Function이 Optimal Value Function 이기 때문에,
이러한 Self-Consistency 조건은 특정 Policy와는 상관없는
아래와같은 특별한 형태로 표현될 수 있습니다.
(V(s) = max_πV(s,a)이나,
이말은 곧 a가 Maximum한 Value를 찾는 행동으로 고정되므로...)

즉, 이를 q*(s,a)에서, v*(s`)에 대입해주면,
최적 Q Bellman Equation을 도출할 수 있습니다.

이것을 벨만 최적 방정식 (Bellman Optimality Equation)이라고 부릅니다.
+
대비되는 개념인 벨만 기대 방정식 (Bellman Expectation Equation)은
q*(s,a) = E [ Rt+1 + γ *Σ_a' π(a'|s') Q(s', a') ]로,
벨만 최적 방정식 처럼 γ * max_a` Q*(s`,a`) 즉, 최대Q가 되는 값만을 Update하는 것이아니라
모든 행동에 대한 Q값 Σ_a' π(a'|s') Q(s', a')을 통해 평균값을 Update하는 것을 의미합니다.
식을 보면, 책에서
State, Action Value Function에서
각각 두가지 형태의 최적 벨만 방정식을 각각 제시한 것을 알 수 있는데,
환경모델에 대한 모든 정보를 알고있어서
어떤 Probability로 State가 변하고 어떤 Reward를 받을지 알 수 있을때,
Model Based 한 관점에서 가치를 추정하는 "Planning" 형태와,
환경모델에 대한 정보 없이 지금까지 들어온 모든 정보를 이용해 기대값으로 가치를 추정하는 "Learning"형태의
벨만방정식을 제시한 것을 알 수 있습니다.
V*와 q* 각각에 대한 보강다이어그램은 아래와 같습니다.
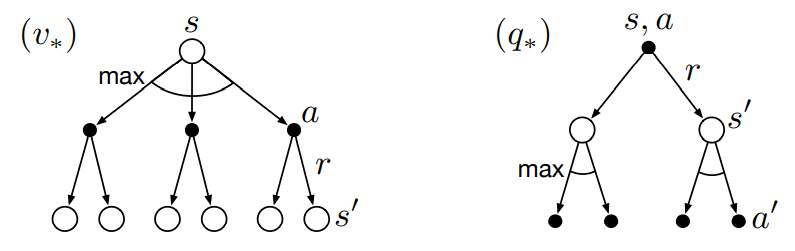
유한 MDP에 대해서, V*를 위한 최적 벨만 방정식은
Policy와는 별개로 유일한 해를 갖습니다.
그리고 최적 벨만 방정식은 각 상태마다 하나의 방정식으로 구성되어있습니다.
즉, n개의 상태가 있으면 n개의 미지수에 대한 n개의 방정식이 존재하는 것입니다.
원칙적으로는 환경모델에대한 정보에 해당하는 p를 알면,
비선형 방정식을 푸는 다양한 방법중 하나를 이용해서 V*를 구하기 위한 방정식을 풀 수 있습니다.
(요약때 정리하겠지만, 이건 거의 불가능하기 때문에 '원칙적으로는'이라는 표현이 사용되었습니다)
일단 (State Value Function) V*를 구하면, 쉽게 최적행동을 정의할 수 있습니다.
각 State에서 단일단계 탐색(One Step Ahead Search)이후 가장 좋은 것처럼 보이는(더 큰 State Value를 가지는) State로 가게끔 행동을 선택하는 것이 최적 행동이 됩니다.
'One Step Ahead Search'이후에 가장 좋은 행동을 선택하는것을 다른말로하면
'Greedy'한 Policy라고 할 수 있습니다.
이러한 Greedy Policy는 미래를 내다보지 않고, 당장 현재에 가장 좋은 것만을 선택하는 것인데,
Bellman Equation에서는 이런식의 Greedy한 Policy를 취하는 것이 장기적인 측면에서도 최적의 결과를 가져오게 됩니다.
이는 V*에 미래에 일어날 수 있는 모든 행동의 보상 결과가 이미 반영되어있기 때문입니다.
(마르코프 특성이랑 연관있는것같은데 확실하진 않습니다!)
(Action Value Function)Q*가 최적 행동을 선택하도록 만드는 것은 이보다도 훨씬 더 쉽습니다.
Q*만 있으면 에이전트는 One Step Ahead Search 조차도 할 필요가 없이,
모든 상태에서 q*(s,a)를 최대로 만드는 행동을 간단하게 찾을 수 있습니다.
단순히 상태가 아니라 상태-행동쌍의 함수에대한 보상의 기대값을 표현하는 수고를 통해 최적 행동가치함수 (Q*)는
어떤 상태로부터 파생되는 State, 그 State의 Value, 즉, 환경모델에대한 어떤 정보도 알 필요없이 최적 선택을 할 수 있도록 해줍니다.
※ 참고
최적 벨만 방정식을 이렇게 해석적으로 푸는 것은
최적 정책을 찾기위한 하나의 방법이고,
따라서 결국 강화학습 문제를 푸는 것입니다.
하지만 이렇게해서 의미있는 해를 찾게되는 일은 거의 일어나지 않습니다.
이렇게해서 해를 찾는 것은 아래 3가지의 가정을 하고 있기 때문입니다
º 환경모델(환경의 동역학)을 정확히 알고 있다.
º 해의 계산을 완료하기 위한 충분한 계산능력이 확보되어있다.
º 마르코프 성질을 가정한다.
보통 첫번째와 두번째가정을 한번에 만족하기가 정말 어려운데요,
환경의 동역학을 정확히 알 수 있다고 하더라도, State의 경우의 가지수가 조금만 복잡해져도
전체 탐색을 해야하는 계산량이 어마어마하게 늘어나기 때문입니다.
많은 종류의 의사결정 방법은
결국 '근사적으로' 최적 벨만 방정식을 푸는 방법이라고 생각할 수 있습니다.
※최적성과 근사는, 결국 위에서 했던 논의와 같아서 생략.
3장은 유독 연습문제가 많아서,
다음 포스팅에 연습문제에대해 한번더 포스팅하고 요약하도록 하겠습니다.
'AI > Reinforcement Learning' 카테고리의 다른 글
| 단단한 강화학습 Chapter5_몬테 카를로 방법 (Monte Carlo Methods) (0) | 2023.04.11 |
|---|---|
| 단단한 강화학습 Chapter4_동적 프로그래밍 (Dynamic Programming) (1) | 2022.11.02 |
| 단단한 강화학습 Chapter3_(1) _유한 마르코프 결정 과정(Finite Markov DecisionProcesses) (1) | 2022.10.03 |
| 단단한 강화학습 Chapter2_(2) _다중선택(Multi-armed Bandits) (0) | 2022.10.02 |
| 단단한 강화학습 Chapter2_(1) _다중선택(Multi-armed Bandits) (0) | 2022.10.01 |




