정리노트
단단한 강화학습 Chapter2_(2) _다중선택(Multi-armed Bandits) 본문
단단한 강화학습 Chapter2_(2) _다중선택(Multi-armed Bandits)
Krex_Kim 2022. 10. 2. 17:39지난 포스팅에 이어서 쭉 진행해보도록 하겠습니다.
◆목차
◎ 긍정적 초깃값 (Optimistic Initial Values)
◎ 신뢰 상한 행동선택 (Upper-Confidence-Bound Action Selection) (UCB)
◎ 경사도 다중선택 알고리즘 (Gradient Bandit Algorithms)
◎ 연관탐색 (Associative Search (Contextual Bandits))
◎ Chapter_2 Summary
◎ 긍정적 초깃값 (Optimistic Initial Values)
이전 포스팅에서 살펴본 모든 방법 (Stationary, Nonstationary상황에서 표본평균법, 고정된 시간 간격 방법)들은
초기 행동 가치 값(Initial Action Value Estimates)에 어느정도 편중되어(Biased)있습니다.
표본평균 방법에서는 일단 모든 방법이 최소한 한번이라도 선택되고 나면 이 Bias는 사라지지만,
고정된 α 값을 이용하는 방법에서는 편차가 줄어들긴 하지만 계속 지속됩니다.
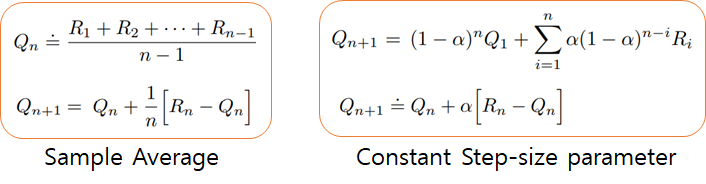
여기에서의 Bias는 학습에 꼭 나쁜쪽으로 영향을 미치는게 아니라 반대로 도움이 되기도 합니다.
이번 섹션에서 다루는 긍정적 초깃값(Optimistic Initial Value)처럼 오히려 학습의 한 테크닉처럼 활용될 수도 있습니다.
앞선 포스팅에서 다뤘던 10중 선택 테스트에서,
https://roboharco12.tistory.com/54
단단한 강화학습 Chapter2_(1) _다중선택(Multi-armed Bandits)
강화학습과 다른 학습과의 가장 큰 차이점은 강화학습은 "정답(Label), 올바른 행동"을 학습할때 '지침(Instruction)'이 아니라, '평가(Evaluation)'하는 정보를 사용하여 학습한다는 것입니다. 지침적인(I
roboharco12.tistory.com
만약 행동가치의 초기값이
모두 0이 아니라 모두 5로 ([0,0,0,0,0,0,0,0,0,0] → [5,5,5,5,5,5,5,5,5,5]) 설정한다고 가정해봅시다.
문제에서, Reward는
"시간단계 t에서 행동 a = At를 선택할때, 실제 Reward값 Rt는 평균이 q*(At), 분산이 1인 정규분포에 따라 선택"
"각각의 문제상황에 대해, q*(a)가 평균이 0이고 분산이 1인 정규분포에 따라 선택."
두가지 조건에 의해서 정의내려졌습니다.
즉, 행동가치의 초기값을 모두 5로설정하면,
a = 1~10중, 어떠한 선택을 하더라도 5보다 큰 Reward를 얻을 확률이 매우 적고,
(아주 아주 높은 확률로 Rt < Qt)
결국 초반엔 어떤 행동을 선택하더라도 Agent가 '실망(Regret)'해서 다른 행동을 선택하게 됩니다.
이러한 방식을 통해 탐험(Explore)을 촉진하는 방법을 "긍정적 초기값 (Optimistic Initial Value)"라고 합니다.
"긍정적 초기값 (Optimistic Initial Value)"으로 초기 가치값을 설정하게 되면,
Action Value값이 수렴하기전에 더 많은 행동을 시도하게 되므로,
행동 선택이 Greedy하더라도 꽤 많은 양의 탐험을 수행하게 됩니다.

위 그림은 10중 선택 테스트 문제에서,
긍정적 초기값(Optimistic Initial Value)으로 행동가치를 설정한 것과,
반대로 현실적 초기값(Realistic Initial Value)으로 행동가치를 설정한 것의 성능차이를 나타내는 그래프입니다.
초기에는 긍정적 방법이 더 많이 탐험하기 때문에 성능이 좋지못하지만, 시간에 따라 탐험이 줄어들기에 궁극적으로 더 좋은 성능을 보여줍니다.
이런 "긍정적 초기값 Optimistic Initial Value" 기법은
정상(Stationary)문제에는 꽤 효과적일 수 있는 간단한 방법이나,
시간에 따라 Reward의 분포가 달라지는 비정상(Nonstationary)문제에서는 적합하지 않습니다.
왜냐하면, 초반에만 일시적으로 탐험을 시도할 뿐이고, 이후 초기값에대한 영향이 줄어들 수록
본질적으로 이전 방법과 다를 것이 없기 때문입니다.
Reward 보상분포가 나중에 달라져서 새로운 탐험이 필요하더라도, 이러한 긍정적 초기값 방법이
새로운 탐험을 촉발하지는 않습니다.
◎ 신뢰 상한 행동선택 (Upper-Confidence-Bound Action Selection) (UCB)
앞선 포스팅에서 정리한 ε-Greedy 방법은,
1-ε의 확률로
Argmax(Q(At))가 되는 행동(탐욕적) At를 취하고,
ε의 확률로
그 외 나머지 행동(비탐욕적)에대해 랜덤으로 행동을 취하는 방법입니다.
여기서 지금까지의 방법대로라면 ,
비탐욕적 행동을 고를때, 모두 동등한 확률로 차별없이 비탐욕적 행동들 가운데 한가지를 고르게 됩니다.
이렇게 하지않고
"나머지 비 탐욕적 행동 가운데 행동가치의 추정값이 얼마나 최대치에 가까운지, 추정의 불확실성은 어느정도 되는지 고려하여 실제로 최적행동이 될 잠재력에 따라서 비탐욕적 행동중 하나를 선택하는 것"
이 더 좋습니다.
이를 신회 상한(Upper-Confidence-Bound, UCB)행동선택이라고 합니다.
이렇게 하기위한 식은 아래와 같습니다.

Nt(a)는 t 시각 이전에 행동 a가 선택된 횟수를 나타냅니다.
아래의 일반적인 greedy한 Action Selection 방법과 비교해보면,

c√ln(t)/Nt(a)
텀이 추가된 것을 확인할 수 있는데, 이를 정리해보면
º c는 상한의 신뢰 수준을 결정함
º Nt(a), 즉, 해당 행동의 표본 개수가 증가함에 따라서 추정의 불확실성이 낮아지는 것으로 생각할 수 있음.
º a 가 아닌 다른 행동이 선택될 때마다 분자에 있는 시간 t는 증가하지만 Nt(a)는 증가하지 않음. 불확실성의 증가.
º 자연 로그를 사용했다는 것은 증가량이 시간에 따라 감소하나, 상한없이 계속 증가함
-> 결국, 모든 행동이 선택되지만 더 작은 가치 추정값을 갖는 행동이나 이미 자주 선택된 행동은 시간에 따라 선택되는 빈도수가 작아질 것임.
10중 선택 테스트에서 UCB를 적용하면 아래와같은 결과를 얻을 수 있습니다.
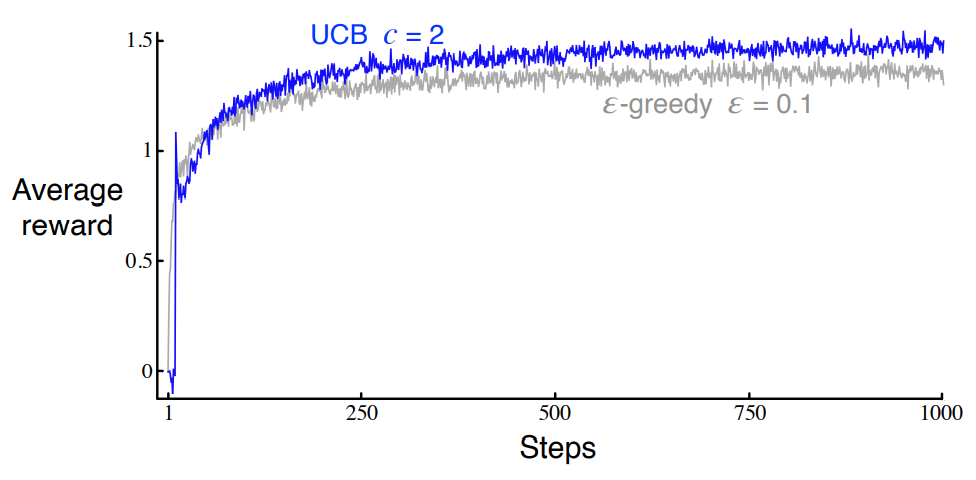
다만 이방법 역시 단점이 존재하는데,
일반적인 강화학습 문제로 확장하여 적용하는데 있어서는 입실론 탐욕적 방법 보다 더 어렵다는 것입니다.
UCB 방법은
일반적인 강화학습 문제인 'Nonstationary'문제,
큰 상태공간(State Space)를 다루는데(이건 아마도 동역학 시스템에서의 이야기인듯합니다.)에는
적용하기 어려운 방법이라고 합니다.
◎ 경사도 다중선택 알고리즘 (Gradient Bandit Algorithms , Softmax Action Selection)
Chapter2에서 지금까지 다룬 내용은,
행동의 가치(Value)를 추정하고 그 추정값을 이용하여 행동을 선택하는 방법들에 관한 것들입니다.
행동을 결정할때 이러한 접근법만 가능한 것은 아닌데요,
경사도 다중선택 알고리즘은
가치(Value)가 아니라 선호도(Preference)에 의한 행동선택을 학습하는 알고리즘입니다.
선호도(Preference)가 클 수록 해당 행동을 더 자주 선택하지만, 선호도와 보상은 다른 개념입니다.
제가 정리하기로는,
가치에의한 행동 결정 방법은 절대적 수치에 따른것이라면,
선호도에 의한 행동 결정 방법은 Softmax 함수를 이용한 상대적 수치에 따라 행동을 결정하는 것이라고 정리했습니다.
Softmax 함수의 형태는 아래와 같고,

여기서 각 행동의 선호도로 정의 되는 Ht(a)는 아래와같이 갱신됩니다.

º 𝝿(a)는 시간단계 t에 Action a가 선택될 확률을 의미함.
º 처음에는 모든 행동의 선호도가 같음. ex ) H1(a=1~10) = 0
º Rt는 시간단계 t에서 행동 At를 선택한 후 받게되는 Reward, R¯t항목은 시각 t 까지의 모든 보상에 대한 평균
º α는 Step Size Parameter
At를 선택한후 받게되는 보상 Rt가
지금까지의 모든 보상에대한 평균 값 R¯t 보다 크게되면, 미래에 At를 선택할 확률은 증가하게 되고,
반대로 작다면 그 확률은 감소하게 될 것입니다.
경사도 다중선택 알고리즘(The Bandit Gradient Algorithm)은 사실
경사도 증가(Gradient Ascent)에대한 Stochastic Approximation과 같은데요,
※ 인공지능에서는 보통 Gradient Descent가 익숙해서 저도 조금 헷갈렸는데, Gradient Descent 는 아래로 Convex한 형태의 함수, Gradient Ascent는 위로 Convex한 형태의 함수에서 수렴값을 찾을때 쓰는 것으로 저는 이해했습니다.
수식을통해 이를 간단하게 정리해보겠습니다.
선호도Ht(a)에 따라 보상의 기대값을 최대화 하고 싶을때,
Ht(a)값을 경사도 증가법에따라 Update한다면 아래와 같이 수식을 쓸 수 있습니다.

그리고 이때 보상의 기대값은

지금까지의 다중선택 문제에서 q*(a)를 정확히 알 수는 없고 추정할 수만 있었습니다만,
본질적으로 기댓값이라는 것에있어서 같게됩니다.

이에대한 증명은 책에있는데 일단 여기서는 Skip하도록 하겠습니다.
◎ 연관탐색 (Associative Search (Contextual Bandits))
앞선 포스팅에서, Chapter2에서는
"강화학습의 평가적인 측면을 단순한 비연합구조(Nonassociative)에서 살펴본다"고 정의 했었습니다.
비연합 구조에서의 학습은,
"학습이 이루어 지는 상황이 State-> Action ->Reward 한번에 대한 것을 다룰때"이므로,
하나의 가장 좋은 행동을 찾으려고 합니다.
즉, 서로다른 행동을 서로다른 상황에 연관 시킬 필요가 없기 때문에 이를 비연합 구조(Nonassociative)라고 책에서 표현했습니다.
그러나 실제 강화학습이 직면하는 문제는 연합구조(Associative)인 경우가 많습니다.
가령, 해당행동이 그 순간의 보상에만 영향을 주는 것이 아니라, 다음 상황에도 영향을 미치게되는 것입니다.
이런상황에서는 하나의 상황에 대해서만 학습이 이루어진다면 전체적으로 제대로된 행동을 수행할 수 없습니다.
강화학습에서 정책이란,
어떤 상황으로 부터 그 상황에 맞는 최고의 행동들을 도출하는 대응관계를 말합니다.
그리고 완전한 강화학습문제는
이러한 정책이 한번의 행동이 아니라 여러번의 보상에대한 기대값을 최대화 할 수 있도록 학습하는 문제를 말합니다.
이 섹션에서 소개하는 연관탐색(Associative Search)은
완전한 강화학습 문제와 비연합구조 문제에 사이에 있는 학습방식으로,
해당 문제가 어떤문제인지 그 정체성에대한 독특한 단서를 얻어내서
각각의 문제를 비연합구조로 학습시킴으로서 정책을 학습시키는 방식을 의미합니다.
정책에대한 학습을 포함한다는 점에서는 완전한 강화학습 문제와 같으나,
각 행동이 바로 그순간의 보상에만 영향을 준다는 점에서는 비연합구조의 문제와 같습니다.
◎ Chapter_2 Summary
Chapter 2에서는 한번 행동하는 상황에대해 학습하는 비연합적 구조(Nonassociative)의 문제에서,
탐험(Explore)과 활용(Exploit)사이의 균형을 맞춰서
Stationary, Nonstationary 각 상황에서 보상을 최대화 할수 있도록 하는 간단한 학습법에대해 다루었습니다.
지금까지의 내용을 간단히 요약해보면 아래와 같습니다.
º ε-greedy 방법은 ε만큼의 좁은 시간구역을 무작위로 선택하여 비 탐욕적으로 탐험하도록 하는방법
º UCB 방법은 행동을 선택할때 Deterministic하게 선택하지만, 각 단계에서 그때까지 얻은 표본의 수가 더 적은 행동을 미묘하게 선호함으로서 Explore하도록 함.
º 경사도 다중 선택 알고리즘(Gradient Bandit Algorithms)은 행동의 가치(Value)가 아닌 선호도(Preference)를 기반으로
Softmax Function을 활용하여 등급에 따라 확률적 방식으로 더 선호되는 행동을 선택함.
º 초기 행동가치 추정값을 긍정적으로 높게 해둠으로서, 초반에 발생하는 행동선택에 대해 대부분 후회(Regret)하게 만듦으로서 탐험(Explore)을 유발할 수 있다.

'AI > Reinforcement Learning' 카테고리의 다른 글
| 단단한 강화학습 Chapter3_(2) _유한 마르코프 결정 과정(Finite Markov DecisionProcesses) (1) | 2022.10.09 |
|---|---|
| 단단한 강화학습 Chapter3_(1) _유한 마르코프 결정 과정(Finite Markov DecisionProcesses) (1) | 2022.10.03 |
| 단단한 강화학습 Chapter2_(1) _다중선택(Multi-armed Bandits) (0) | 2022.10.01 |
| 단단한 강화학습_intro (0) | 2022.09.30 |
| DRL_Introduction_(4) Value Based Approach_2 (0) | 2022.08.30 |




