정리노트
단단한 강화학습 Chapter2_(1) _다중선택(Multi-armed Bandits) 본문
단단한 강화학습 Chapter2_(1) _다중선택(Multi-armed Bandits)
Krex_Kim 2022. 10. 1. 23:23강화학습과 다른 학습과의 가장 큰 차이점은
강화학습은 "정답(Label), 올바른 행동"을 학습할때
'지침(Instruction)'이 아니라, '평가(Evaluation)'하는 정보를 사용하여 학습한다는 것입니다.
지침적인(Instructive) 피드백은 실제로 취해진 행동과는 상관없이 취해야할 행동을 알려줌으로서 학습이 진행됩니다.
일반적인 Machine Learning알고리즘의 학습법이 여기에 해당합니다. 반면, 평가적인(Evaluative) 피드백은 취해진 행동이 얼마나 좋은지를 나타낼 뿐 그것이 최고의 행동인지, 최악의 행동인지는 알려주지 않습니다.
정리하면,
평가적인 피드백은 취해진 행동에 전적으로 의존하는 반면, 지침적인 피드백은 취해진 행동과는 무관하게 이루어집니다.
Chapter2에서는 주로 강화학습의 평가적인 측면을 단순한 비연합구조(Nonassociative)에서 살펴봅니다.
비연합 구조란 "하나의 상황에 대해서만 학습이 이루어지는 구조" 를 의미합니다.
(말이 조금 어려운데,
'학습이 이루어 지는 상황이 State-> Action ->Reward 한번에 대한 것을 다룰때'로 저는 이해했습니다.)
◆목차
◎ 다중 선택 문제 (A K-armed Bandit Problem)
◎ 행동 가치 방법 (Action-Value Method)
◎ 10중 선택 테스트 (The 10-armed Testbed)
◎ 점증적 구현 (Incremental Implementation)
◎ 비정상 문제의 흔적 (Tracking a Nonstationary Problem)
◎ 다중 선택 문제 (A K-armed Bandit Problem)
- 다중선택문제
먼저, 이번챕터에서 다루는 다중 선택 문제(a K-armed Bandits Problem)가 무엇인지부터 정의하도록 하겠습니다.
다중선택문제의 문제정의는 아래와 같습니다.
º 취할 수 있는 Action의 경우의 수는 K.
º 보상(Reward)을 나타내는 값은 선택된 행동 각각에 정의된 확률분포로 부터 얻어지게됨.
º 이 확률분포가 시간에 따라 변하지 않는 것을 정상상태(Stationary), 변하는 것을 비정상상태(Non-Stationary)로 정의.
º 행동선택의 목적은 일정기간, 예를 들면 1000번의 행동선택을 하는 기간동안 얻어지는 보상(Reward) 총량의 기댓값을 최대화 하는것.
- 가치, Value
다중선택 문제에서, k개의 행동 각각에는 그 행동이 선택되었을때 기대할 수 있는 평균 보상(Reward)값이 할당되는데,
이 평균 보상값을 가치(Value)라고 정의합니다.
시간단계 t 에서 선택되는 행동(Action)을 At로 표현하고, 그에따른 보상(Reward)은 Rt로 표현하면,
임의의 행동 a의 Value q*(a)는 행동 a가 선택되었을때 얻는 보상의 기댓값으로, 아래와같이 정의할 수 있습니다.

※ 만약 모든 행동의 가치를 미리 정확하게 알수있다면 다중선택문제는 그냥 가장 큰 Value를 주는 행동을 선택하면 그만이겠으나, 행동의 가치를 추정할 수는 있더라도 확실히는 알지 못한다는게 전제입니다.
->보상을 나타내는 값이 선택된 행동 각각에 정의 된 확률분포로부터 얻어지는 것.
시간단계 t에서 추정한 행동 a의 가치는 Qt로 표현하는데, 추정값 Qt와 기댓값 q*가 가까워질 수록 정확한 추정이 됩니다.
- 활용(Exploiting) vs 탐험 (Exploring) ( 탐욕적(Greedy) vs 비탐욕적(NonGreedy) )
강화학습에서 Greedy한 행동이란, 최대의 가치를 갖는 행동만을 취하는 것을 말하고,
non-greedy는 그 반대의 상황을 의미합니다.
강화학습에서 행동은 Greedy, Nongreedy 관점에서
활용(Exploiting)과 탐험(Exploring) 2가지 카테고리로 나눌 수 있습니다.
탐욕적 행동을 선택하는 것은 행동의 가치에 대해 현재까지 가지고있는 지식을 활용(Exploiting)하는 것이고,
비탐욕적 행동을 선택하는 것은 그 외의 행동가치를 상승 시킬 수도 있는 것으로, 이것은 탐험(Exploration)하는 것에 해당합니다.
단기적으로 한번의 행동에 대해 최대의 보상을 원한다면 활용(Exploiting)하는 것이 바람직 할 것이고,
장기적으로 보상의 총합을 키우기 위해서는 탐험(Exploration)하는 것이 바람직 할 것입니다.
최적의 학습결과를 얻으려면 활용과 탐험 둘다 적절히 활용해주어야하며,
매 행동선택에서는 둘중 하나의 선택만이 가능하므로, 언제 어떻게 둘을 적절히 분배할 것인지 학습과정에서 잘 설정해주어야 합니다.
◎ 행동 가치 방법 (Action-Value Method)
뒷부분에서 따로 정리하는 부분이나, 미리 먼저 간단하게 정리해보면
Value에는 State의 Value가 있고, Action Value가 있습니다.
아래 포스팅에서 Value Function 섹션에 정리해두었습니다.
https://roboharco12.tistory.com/51
DRL_Introduction_(3) Value Based Approach_1
https://www.youtube.com/watch?v=dw0sHzE1oAc&list=PLldiB_QS6edl3h831ZrSG8crEWOvPWeun&index=4 발표자료 https://www.slideshare.net/NaverEngineering/introduction-of-deep-reinforcement-learning Introduct..
roboharco12.tistory.com
어떤 행동이 갖는 가치(Value)는 행동이 선택될 때 보상의 기대값, 즉, 평균 보상입니다.

= (시각 t 이전에 취해지는 행동 a에대한 보상의 합) / (시각 t 이전에 행동 a를 취하는 횟수)
큰수의 법칙에 의해 해당 행동을 여러번 많이 취하게된다면, Qt(a)는 q*(a)에 점점 가까워지게 됩니다.
행동을 취할때,
이렇게 정의된 가치(Value)를 통해 행동을 결정하는 것을 행동 가치 방법(Action-Value Method)라고 합니다.
행동을 결정할때, 가치가 가장 높은 행동만을 취하는 것을
탐욕적 행동, 'greedy action'이라고 하고, 이는 활용(Exploiting)에 해당합니다.

이와는 반대로,
가치는 낮지만 실제로 높은 Reward를 줄 수 도 있는 행동을 취할 수도 있는데, 이는 탐험(Exploring)에 해당하며,
ε의 비율만큼 탐험(Exploring)하는 것을 ε-Greedy 방법이라고 합니다.
-> ε = 0 이라면, Greedy한 방법의 행동선택이됩니다.
# Epsilon Greedy Action Selection
def act_select(qn,epsilon):
if np.sum(qn)== 0:
return random.randint(0,9)
else:
argmax_num = np.argmax(qn)
other_num = np.delete(np.arange(0,10,1),argmax_num)
output_list = [argmax_num ,np.random.choice(other_num)]
return np.random.choice(output_list,p=[1-epsilon,epsilon])
◎ 10중 선택 테스트 (The 10-armed Testbed)
Chapter2에서 다루는 가장 대표적인 다중선택문제의 예시로,
문제정의는 다음과 같습니다.
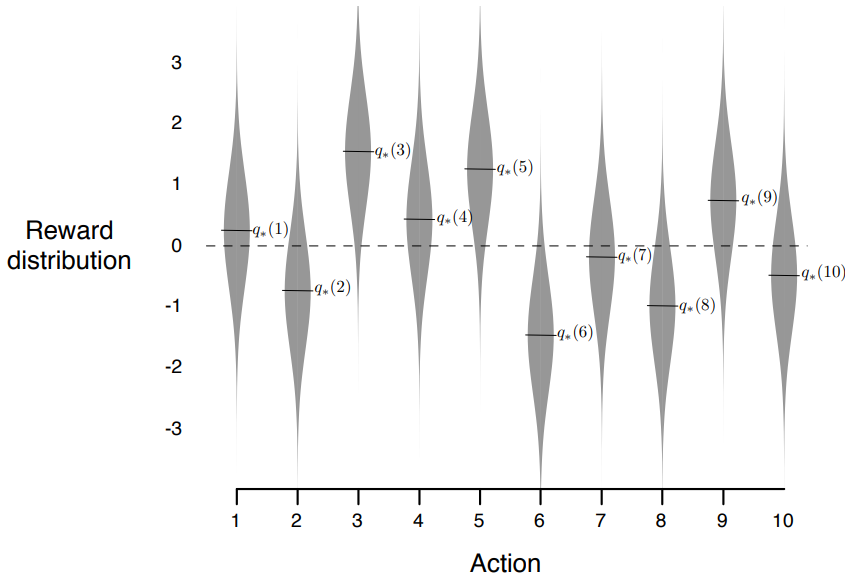
º Action은 10가지 경우의 수(a=1~10), 이러한 문제상황 2000개를 무작위로 생성.
º 각각의 문제상황에 대해, q*(a)가 평균이 0이고 분산이 1인 정규분포에 따라 선택.
º 시간단계 t에서 행동 a = At를 선택할때, 실제 Reward값 Rt는 평균이 q*(At), 분산이 1인 정규분포에 따라 선택.
º 이렇게 2000개의 독립적인 문제를 수행하여 알고리즘의 평균 결과를 측정한 것을 1회의 실행이라고 함.
º 2000개 문제 각각은 1000번의 시간단계를 거치며 학습이 이루어지며,
최종 학습 성능은 2000개의 문제의 1000번의 시간단계 각각의 성능값의 평균을 기준으로 제시함.
(한글 책에서 오역이 한가지 있는데,
'10번의 선택'이 아니라 '10가지 경우의 수중 한가지를 선택'하는 것이 맞습니다.
아무리봐도 이상해서 그냥 원서를 뒤져봤더니.. 오역이 맞았습니다...
이거때문에 연습문제를 통으로 다시풀었는ㄷ...)
-> 이에 대한 예제는 연습문제 2.5에서 자세히 다루고 있습니다.
제가 풀이한 방법도 포스팅 맨아래에 깃허브 링크로 따로 공유놓도록 하겠습니다
이 10중 선택 문제를
행동 가치 방법에서 정의한 ε-Greedy 방법으로 학습을 해보면 아래와같이 ε값에 따른 결과를 비교할 수 있습니다.
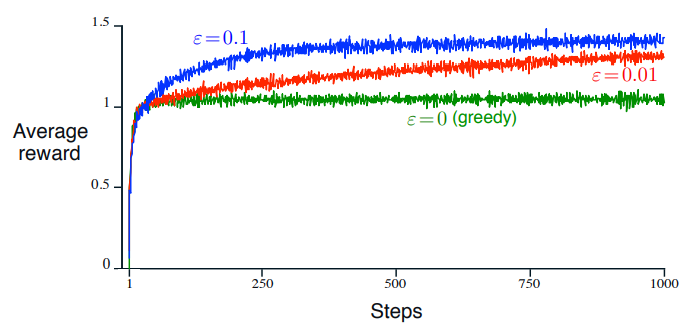
ε값이 작은, 더 Greedy한 값일 수록 시작 직후에 성능은 더 빠르게 증가하지만,
결국 다른방법에 비해 낮은수준으로 떨어지는 것을 확인할 수 있습니다.
앞서 언제 Greedy한 행동을 취할 것이고, 언제 Non-greedy하게 탐험(Explore)할 것인지
정해주는 것이 중요하다고 정리했었습니다.
가령,
보상 Rt에 분산(Noise)이 작을경우, 시간에 따라 받게되는 보상이 크게 달라지지 않으므로,
정확하게 Value값을 추정하는데에 그리 오래 걸리지 않을것이라서
Greedy한 행동을 하도록 ε값이 작은것이 좋을 것이고,
반대로 보상 Rt에대한 분산(Noise)이 클경우, 현재 내가 받게되는 보상에 제대로된 보상분포를 알려면,
즉, 정확하게 Value 값을 추정하려면 어느정도의 여러번 시도가 필요해서
더 탐험을 하도록 ε값이 큰 것이 더 좋을 것입니다.
또한가지,
보상의 분포가 시간에 따라 변하지 않는 경우를 (정상)Stationary 문제,
시간에 따라 변하는 경우를 (비정상)NonStationary문제라고 하였는데,
Nonstationary 문제에 경우, 처음시작할 당시 q*(a)와 시간이 지남에 따라 달라지는 q*(a)도 달라지고, 그에따른 분산도 달라지므로, 탐험이 무조건적으로 필요하게됩니다.
◎ 점증적 구현 (Incremental Implementation)
이제부터, 본격적으로 다중선택 문제를 어떻게 구현하는지에대해 하나하나 살펴보도록 하겠습니다.
지금까지 다룬 행동가치방법(Action-Value Method)는 모두 관측된 보상의 표본평균값을 기준으로 행동의 가치(Value)를 추정하고, 이에따라 행동하도록 하는 것이었습니다.
선택된 하나의 행동에 대해, 해당 행동이 선택된 횟수를 n번 이라고 할때
n-1번 선택된 이후에 이 행동의 가치 추정값은 아래와 같습니다.

이는 표본 n-1개에 대한 보상 Rt의 평균값의 식으로, 모든 보상을 기록해 두고 추정값이 필요할 때마다 이식을 이용해서
가치를 계산하는 것입니다.
이렇게 계산할 경우, 보상이 더 많이 관측될 수록 컴퓨터의 메모리와 계산능력이 추가로 필요하게 되는데,
다른 방식을 이용하면 일정한 계산 능력만을 이용해서 평균값을 갱신할 수 있습니다.
책에서는 이 방법을 아래의 "점증적 공식(incremental formulas)"으로 정리했습니다.

공식자체는 크게 어렵지 않은데요,
이렇게 공식을 적용할 경우,
지금까지 계산된 행동가치 Qn, 현재 Reward값 Rn 두가지만을 이용해 새로운 행동가치 Qn+1을 계산할 수 있게됩니다.
이러한 갱신규칙은 강화학습 전반에서 많이 나타는 형태의 규칙인데,

새로운 추정값 ← 이전 추정값 + 시간간격(목표값 - 이전 추정값)
Value값은 Reward의 평균값으로 정의된 값이고, Reward의 평균 값을 추정하고자 정해지는 값이기때문에
목표값 - 이전 추정값으로 표현한 것은 '오차'가 됩니다.
그리고 이 오차는 시간이 흐르면서 데이터가 많아짐에 따라 감소하게됩니다.
->보다 정확하게 Reward를 추정하게 되는 것입니다.
행동가치 Value를 Update하는 과정을 pseudo Code로 표현해보면 아래와 같습니다.

◎ 비정상 문제의 흔적 (Tracking a Nonstationary Problem)
앞서,
Reward에 대한 확률분포가 시간에 따라 변하지 않는 것을 정상상태(Stationary),
변하는 것을 비정상상태(Non-Stationary)로 정의했었습니다.
그리고 행동가치를 계산할때,
지금까지의 방법 처럼 표본평균값을 통해서 추정하는 방법을 표본평균법 (Sample Average Method)라고 합니다.
이러한 표본 평균 방식은 'Stationary' 다중 선택 문제에 적합한 방식입니다.
그러나, 강화학습 문제의 대부분은 시간이 지남에 따라 Reward에 대한 확률분포가 달라지는 Non-Stationary문제인 경우가 많은데,
이러한 문제에서는 최근 들어온 보상일 수록 더 큰 가중치를 두고, 과거의 보상일 수록 낮은 가중치를 두는게 타당할 것입니다.
가장 많이 사용되는 방법으로는 Constant Step-Size Parameter(고정된 시간간격)을 사용하는 것입니다.

무슨말이냐면, 시간간격 parameter α를 고정된 값으로 두는 것입니다.
(만약 α=1/n이라면, 표본평균방법이 되는 것입니다, 이는 시간단계에 따라 시간간격 크기를 작게 하는 것과 같습니다.)
※ 헷갈리면 안되는게, 시간간격은 가중치가 아닙니다.
이렇게 계산할 경우, Qn+1을 자세히 계산해서 추정해보면,

(1-α)는 1보다 작은값으로, Q1값이 가장 작고, 그 이후 들어오는 Ri값도 시간이 증가함에 따라 1-α배 만큼 계속 작아져서
현재의 추정값에 반영됩니다.
* 이런 가중치를 통해 이후 값을 Update하는 것을 Exponential Recency-weighted Average라고 부르기도 한다고 합니다.
지수 이동 평균과 유사하거나 같은 개념으로 이해하면 될것같습니다.
다음 포스팅에 이어집니다
'AI > Reinforcement Learning' 카테고리의 다른 글
| 단단한 강화학습 Chapter3_(1) _유한 마르코프 결정 과정(Finite Markov DecisionProcesses) (1) | 2022.10.03 |
|---|---|
| 단단한 강화학습 Chapter2_(2) _다중선택(Multi-armed Bandits) (0) | 2022.10.02 |
| 단단한 강화학습_intro (0) | 2022.09.30 |
| DRL_Introduction_(4) Value Based Approach_2 (0) | 2022.08.30 |
| DRL_Introduction_(3) Value Based Approach_1 (0) | 2022.08.27 |




