정리노트
Deep Learning (9)_Convolution Layer 본문
이번 포스팅에서는 Computer Vision에 쓰이는 여러가지 Neural Network중,
매우 큰 Building Block인
Convolution Layer에 대해 다루어 보고자 한다.
◆목차
◎ Computer Vision Problem Types
◎ Building Blocks of CNN
◎ FC(Fully Connected Layer)
◎ Convolution Layer
○ Edge Detection
○ Learning Filters.. to detect Various Edge
○ Convolution with Bias
○ Padding & Stride
○ Summary of Convolutions & Notation
◎ Convolution Over Volume (참고)
◎ Technical note... Convolution in mathbook (참고)
◎ Computer Vision Problem Types
Convolution Layer는 주로 Computer Vision에서 자주 쓰이는 Layer인데,
Computer Vision Problem의 종류는
크게 아래의 4가지로 나눌 수 있다.

- image Classification
: 전체 pixel 데이터로 어떤 이미지인지 Class Label을 알아맞추는 것
- Classification + Localization
: 단순히 전체 pixel이 의미하는 것을 맞추는것이 아니라, 해당 Label을 표현하는 Bounding Box까지 그려주는 것
- Object Detection
: Classification+ Localization을 여러개 합친것,
여러개의 Object에대해 Class Label을 맞추고, Bounding Box를 그려주는 것
- Segmentation : Object Detection보다 더 Challenging 한 Neural Network로,
단순히 Bounding Box를 구하는 것이 아닌, Pixel단위로 어떤 이미지인지 알아맞추는 것.
◎ Building Blocks of CNN
CNN Architecture에 쓰이는 Layer 종류는 크게
Fully Connected Layer, Convolution Layer, Pooling Layer, 3가지로 나눠서 생각할 수 있다.
이에대한 내용은 아래 링크 참조.
https://blog.naver.com/PostView.nhn?blogId=intelliz&logNo=221709190464
[딥러닝 레이어] FC(Fully Connected Layers)이란?
안녕하세요. 인텔리즈 입니다. FC(Fully Connected Layers)레이어에 대해 포스팅합니다. 보통 CNN ...
blog.naver.com
Cnn method
Convolutional Nerual Network
www.slideshare.net

지금부터 이런 Building Block에대해 하나하나 살펴보도록 하자.
◎ FC(Fully Connected Layer)
Fully Connected Layer는,
이전 노드에서가 다음 노드로 데이터들이 Propagation될 때,
모든 노드에 대해서 Propagation되는 Layer를 의미한다.
https://medium.com/swlh/fully-connected-vs-convolutional-neural-networks-813ca7bc6ee5
Fully Connected vs Convolutional Neural Networks
Implementation using Keras
medium.com
하지만 Vision Proble에서 FC만 사용한 Neural network는 절대 효과적인 Network가 될 수 없는데
그 이유는 아래와 같다.
이미지 데이터는 픽셀값 하나하나가 Input Data가 되므로,
Feature Dimension이 기본적으로 매우 큰데,
Fully Connected Layer로만 구성된 Neural Network에서 모든 노드가 이를 받아들일 경우
Parameter수가 너무 비효율적으로 많아져 효과적인 Neural Network가 될 수 없다.

위 예시그림에서, 만약 1000X1000 image를 input으로 Fully Connected Layer에 Propagation이 진행될 경우,
한번 Hidden Layer를 통과하면
->10^6개의 Hidden Units (Input Parameter 10^6개, Output parameter 10^6개)
10^6*10^6 = 10^12개의 parameter가 생긴다.
이런 문제로 Fully Connected Layer로만 구성된 Neural Network는
Computer Vision 분야에서 절대 효과적인 성능을 구현할 수 없는 것이다.
Convolution Layer가 Computer Vision Neural Network에서 핵심적인 Building Block가 된 이유는,
바로 이런 Learning Parameter 개수 문제점을 혁신적으로 해결해주기 때문이다.
◎ Convolution Layer
그렇다면 Convolution Layer란 무엇일까?
앞서 모든 노드와 노드사이를 다 연결하는 Fully Connected Layer와 달리,
Convolution Layer는 아래처럼 Kernel Size에 해당하는 부분만을 한개의 Pixel Data에 Propagation한 Layer를 의미한다.

Convolution Layer가 특별한점은, 바로 이 Kernel Size에 해당하는 부분이
일종의 'inductive Biased Filter'역할을 한다는 점이다.
아래 Edge Detection내용을 통해 무슨말인지 알아보도록 하자.
○ Edge Detection
'Edge'란, 이미지에서 경계가 되는 부분, Pixel 데이터상 변화가생겨서 구분지을 수 있는 포인트가 생긴 지점을 의미한다. 우선 가장 간단한 Edge Detection인 Vertical Edge Detection과 Horizontal Detection에 대해 살펴보도록 하자.

3x3의 Filter Size라고 하였을 때,
작동원리는 아래와 같다.
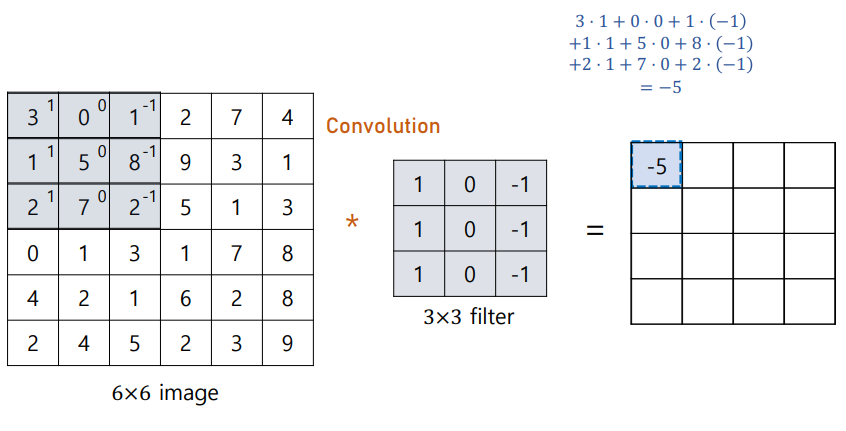
...위의 계산법을 쭉 따라가면

이런식으로 Matrix를 채우다보면,
input image의 좌우 pixel Value의 차이가 큰부분, 즉,
Vertical Edge가 되는 부분은 남고, 별 차이가 없는 부분은 값이 사라지게된다.-> 경계(Edge)부분에 선이 생긴다.

Horizontal Edge Detection도 마찬가지 원리로 진행된다.

가장 단순한 Vertical Edge, Horizontal Edge에 대해 살펴보았는데,
CNN에서는 그 이외에 다양한 Edge를 Detecting하는 Filter를 여러개 만들어서 사용한다.

그리고 여기에 Bias Term까지 추가하면

-> 즉, CNN Layer에서의 Learnable Parameter는,
위에서본 Filter 각각의 Weight와, Bias 두가지가 된다.
-> 이 Weight와 Bias로 이루어진 Filter를 통과했다는 것을
달리말하면 특정 영역의 Pixel에대하여 "Inductive Bias"를 적용하여 Filtering했다는 것과 같은 의미가 된다.
-> Neural Network에서 Back Propagation을 통해 학습시키는 행위가 곧,
CNN에서는 어떤 종류의 Filter가 될지에 대해서 학습시키는 것과 같아지는 것이다.
* 참고: Lee, Honglak, et al. "Unsupervised learning of hierarchical representations with convolutional deep belief networks."
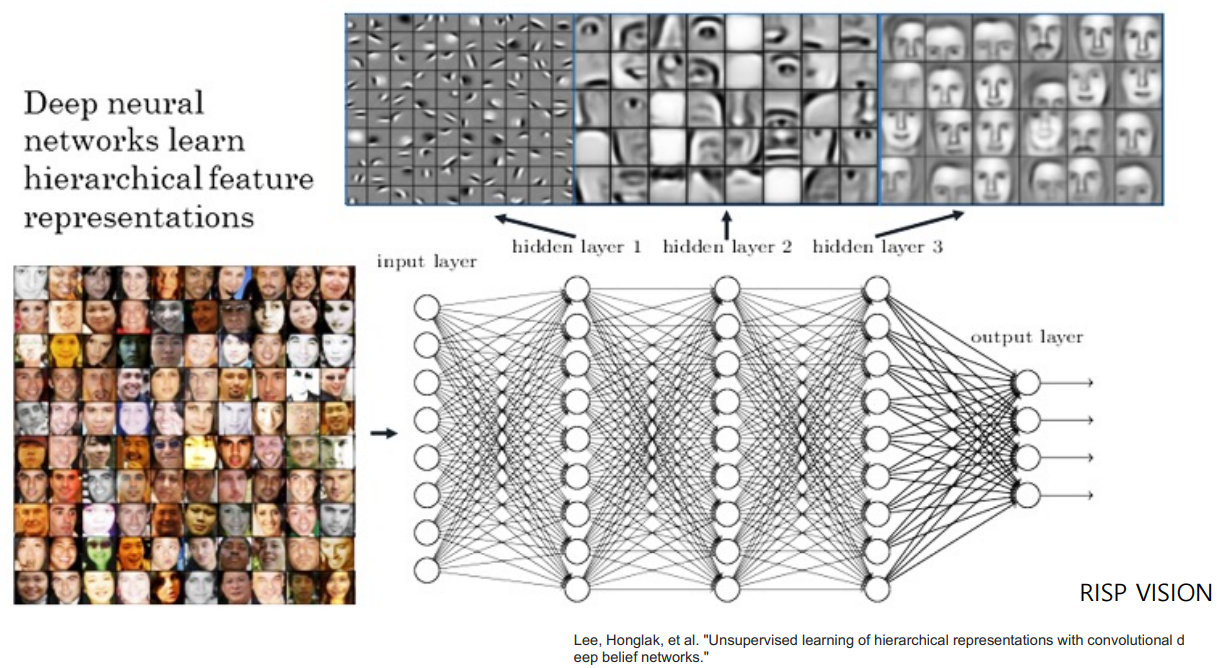
일반적으로 CNN Hidden Layer에서,
더 낮은 단계의 Layer일수록 세밀한 Edge, Curve같은 저수준의 특징을 Filtering하고,
더 높은단계의 Layer일수록 Texture, Object Parts(물체의 일부분)을 골라내는 고수준의 특징을 Filtering하는 것으로 알려져있다.
○ Padding & Stride
지금까지 Convolution Layer의 Filter가 어떻게 작동하는지 작동원리에 대해 다뤄보았다.
이런 필터로 학습시킬때, 정해주어야하는 것이 몇가지 있는데, 그중 Padding 과 Stride를 살펴보도록 하겠다.
- Padding
Convolution Layer에서는 아래 그림에서 처럼 Layer가 쌓이면 쌓일 수록 Mapping되는 image의 size가 줄어들 수 밖에 없게된다.

이런 단점을 보완하고자 원본 pixel에 p Size만큼 Pixel을 더 추가해주는 것을 바로 'Padding'이라고 한다.

그리고 위 이미지에서 처럼 output size와 input size가 똑같게끔 p size를 설정해 주는 것을
"Same Padding"이라고 한다.

- Stride
Stride는 Filter가 Pixel을 이동하는 단위를 의미하는 것으로, 아래 그림처럼 이해하면 된다.

○ Summary of Convolutions & Notation
지금까지 다룬 Convolution 내용을 요약하면, 아래와 같다.

이에대한 Notation은 아래와같이 요약할 수 있다.

◎ Convolution Over Volume (참고)

input이 3차원이면, Filter도 그에맞는 3차원이어야하고, 마지막 Volume은 그 개수를 똑같이 맞춰줘야한다.

이런 Filter를 여러개쓰면 Output Size도 다시 3차원으로 활용해서 쓸 수 있다.
◎ Technical note... Convolution in mathbook (참고)
https://supermemi.tistory.com/104
[ Math ] Convolution(합성곱)의 원리와 목적
[ Math ] Convolution(합성곱)의 원리와 목적 Convolution Convolution (합성곱) 많이들 들어 보셨을 겁니다. 의미적으로는 두 함수를 서로 곱해서 합한다는 것이지요. 합성곱을 공부하셨다면 아래의 질문
supermemi.tistory.com
Convolution의 원래식은 아래와 같고,

함수 f가 주어졌을때 목적에 맞게 g를 선택하여 분해, 변환, 필터링하는것을 Convolution(합성곱) 이라 한다.

위 그림에서
[3,4,5]
[1,0,2]
[-1,9,7]와
[7,9,-1]
[2,9,1]
[5,4,3]은
좌우위아래로 완전히 반전시킨 형태로, 두개의 필터를 한번에 사용하면 수학적 의미의 Convolution Filter가 된다.
* CNN에서는 크게 의미가 없는게 Fixed된 Filter를 쓰는게아니라 Learnable Parameter로 Filter의 Weight를 학습시키기 때문에, 내용이 전혀 다르다 -> 그냥 참고정도만 하면 될거같다.
* CNN의 3번째 Building Block인 Pooling Layer는.. 글이 너무 길어진 관계로
다음 포스팅 CNN(Convolution Neural Network)부터 다뤄도록 하겠다.
'AI > Deep Learning' 카테고리의 다른 글
| Deep Learning (11)_CNN_2.. LeNet-5, Alex Net, VGG Net (0) | 2022.05.22 |
|---|---|
| Deep Learning (10)_CNN (Convolution Neural Network)_1 (0) | 2022.05.22 |
| Deep Learning (8)_Tensorboard & Tuning Parameter (0) | 2022.05.21 |
| Deep Learning (7) _Batch Normalization (0) | 2022.05.21 |
| Deep Learning (6) _Optimization (0) | 2022.04.23 |




