Machine Learning에 필요한 기초지식 - Probability Overview(2)- Jointly Distributed Random Variables

이전 포스팅 (1)에서는 Random Variable하나를 가지고 어떤 확률분포를 따르는지,

혹은 가정하는지에 대해 간단히 다뤄보았다.

 

이번 포스팅에서는 여러개의 Random Variable에관한 내용이며,

큰 줄기로는 다음 포스팅에 다룰 Bayes Classifier를 이해하기위한 개념들을 정리해볼 것이다.

 

◆목차

◎ Jointly Distribured Random Variables(결합 확률변수)

◎ Conditional distribution

◎ Independent Random Variables

 

 

 

 

 

◎ Jointly Distribured Random Variables(결합 확률변수)

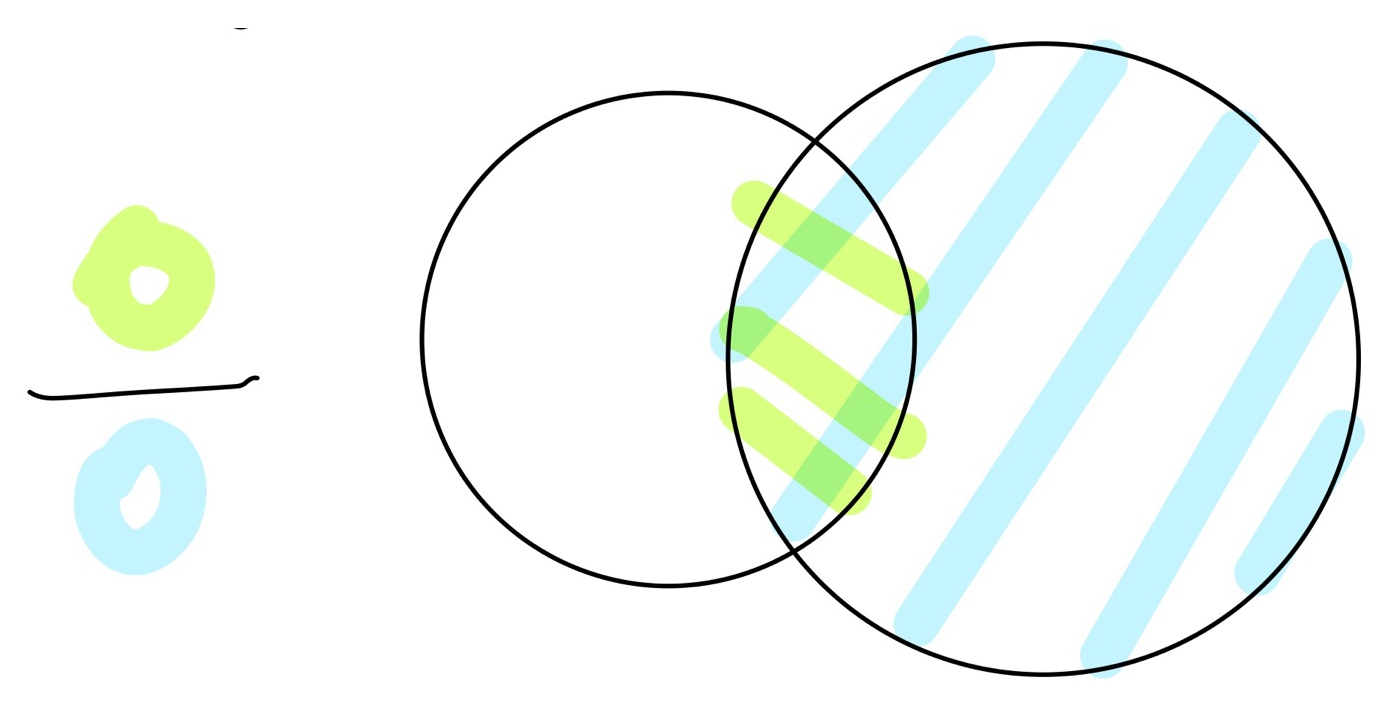
'결합'확률 분포는 여러개의 Random Variable의 확률변수를 종합해서 고려한 확률 분포를 의미한다.

기호로는 교집합 기호 P(X∩Y) 를 쓰거나 P(X,Y) 쉼표 또는 P(X = x and Y = y)와 같이 'and'를 이용해 표기한다.

 

◎ Independent Random Variables

Random Variable끼리 서로 독립적이라면, 단순하게 두 확률 분포값을 곱해서 Jointly Distribution을 구하면 되겠지만,

대개의 경우 Random Variable끼리는 어느정도 서로 종속적인(Dependent Case) 경우가 많다.

예를들어, '단과대학 종류'와 '남녀성비' 두가지 Feature가 있다고 했을때, 보통 공학대학의 경우 남자가 압도적으로 비율이 많으므로, P(남자,공학대학)을 구하고 싶을때 P(남자) X P(공학대학) 으로 구하면 실제와 다른 확률이 구해진다.

 

-> 학교인원이 300명, 전체 남 여 비율은 1:1 이며, 단과대학교는 공과대학, 자연대학, 언어대학 3개대학교에 각 인원은 100명씩 있고, 그중 공학대학의 남녀성비는 9:1 이라고 가정하자.

P(남자∩공학대학)의 실제 확률은 100*0.9/300 = 0.3이다.

그러나, P(남자)*P(공학대학)으로 계산한 확률은 0.5*(1/3) = 0.166.. 으로 완전히 다른값이 도출된다.

 

 

◎ Conditional Distribution

'조건부 확률'. 어떤 사건이 벌어졌다는 가정하에 다른 특정한 사건이 발생할 확률을 의미하며,

아래와같이 표기한다.

 

 

이때, 오른쪽 항 분자의 해당하는 Pxy(X,Y)의 값은 , X, Y가 Continous한지, Discrete한지에 따라서 값이 다른데,

그 값은 Continous의 경우 PDF(Probability Density Function), Discrete의 경우 PMF(Probability Mass Function)를 따른다.

 

아래 내용은 

둘다 Continous,

둘다 Discrete,

둘중 하나씩 Continous, Discrete,

3가지 경우로 Probability Function을 계산하는 법에대한 내용이다.

 

 

○ 두 Variable이 모두 Discrete할 때 PMF(확률 질량 함수)

Sample Space Ω 중, A라는 결과가 도출 될 확률은 

모든 Discrete한 확률을 더해주면 된다. 

 

 

○ 두 Variable이 모두 Continous할 때 PDF(확률 밀도 함수)

Discrete Case처럼 단순히 더하여 Joint Probability를 구할 수는 없다.

Sample Space는 Continous한 구간으로 이루어져 있고, 이 구간 사이에는 무한히 많은 Variable이 존재하므로

각 Sample의 확률은 0으로 수렴하기 때문이다. 즉, Continous Random variable Case에서는 Joint Probability를 적분을 이용해서 구한다.

 

 

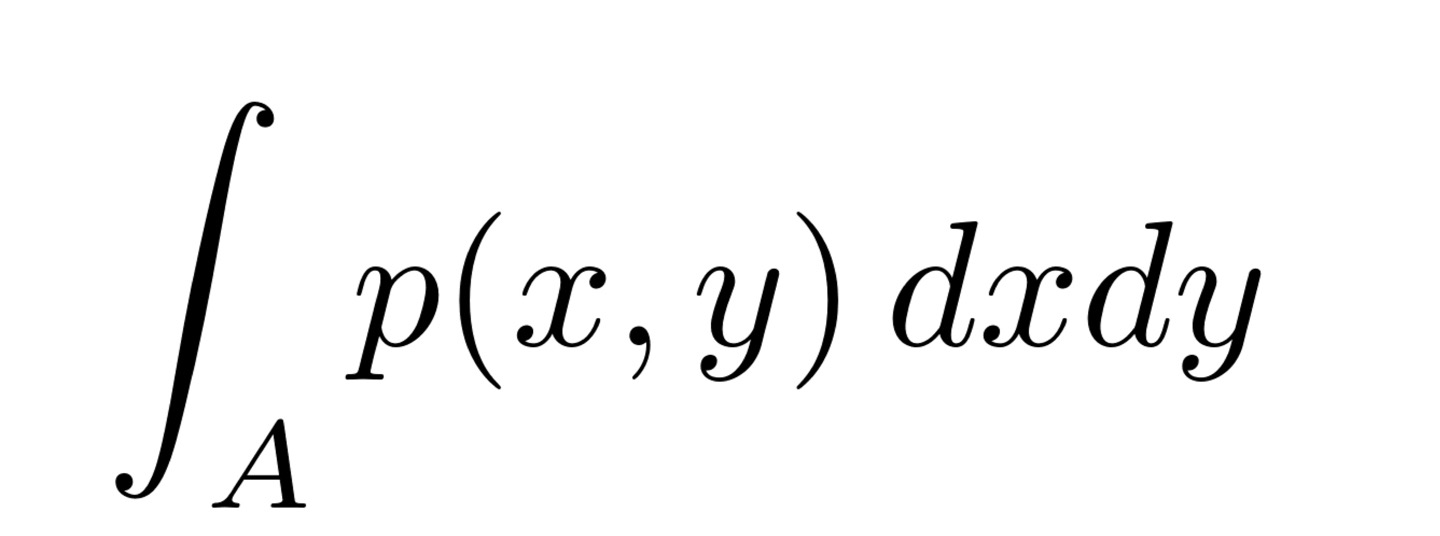
○ 둘중 하나씩 Continous, Discrete(Mixed Case) 한경우의 Probability Function

여기서부터는 (교수님 왈) 근본이 없다고 한다

두개의 변수 특성이 다르므로, PDF와 PMF는 더이상 의미가 없지만,

 

Sample이 'A'사건일 'y'의 확률에 대한 margin out

위처럼 조건부 확률을 이용해 특정 사건의 확률을 'margin out'하는 Operation은 그래도 유효하다.

아래 예제를 통해 이를 이해해 보도록 하자.

 

Normal Distribution ..... N(평균,분산)    Bernoulli는 Bernoulli Trial에서의 확률을 의미함.

예제에서 Y는 베르누이 시행에서의 확률값이며 Sample Space가 {0,1}이고, Py(1) = 1/3 이므로 Py(0) = 2/3 가 된다.

X는 Continous Random Variable일때, P(x)의 Probability Function을 구해야 하는게 문제다.

 

위의 y에대한 'margin out'을 이용해주면 아래와같이 풀이가 가능하다.