Machine Learning에 필요한 기초지식 - Probability Overview(1)- Random Variable

◆목차

◎ Random Variable(확률변수)

○ Discrete Random Variable 

○ Continous Random Variable 

○Expectation

 

 

◎ Random Variable

확률변수의 의미는, Random한 실험이나 관측등을 진행했을 때, 그 변수의 값이 존재할 확률을 수치적으로 표현한 변수를 의미하며, 이때 존재가능한 모든 변수의 값의 집합을 Sample Space라고 한다.

Random Variable의 종류는 크게

연속된 값을 표현하는 변수(Continous)와 불연속적인 값을 표현하는 변수(Discrete) 두가지로 나눌 수 있다.

Continous Random Variable와 Discrete Random Variable은 각각 Continous Sample Space와 Discrete Sample Space를 가진다.

 

그리고 이때 변수값의 존재확률은 확률 분포를 따르는데,

Continous Random Variable의 경우 PDF(Probability Density Function),

Discrete Random Variable의 경우 PMF(Probability Mass Function)라고 하고,

이는 상황에 따라서 각각 다르게 적용된다.

보통 Uniform하거나, Gaussian Distribution을 따르거나인데,

그 예시는 아래에 정리해두었다.

 

 

○ Discrete Random Variable 

- Discrete Uniform Distribution

: 'Uniform Distribution', 즉, 모든 확률이 동일할때의 확률분포를 의미한다. 예를들어 정육면체 주사위를 던졌을 때, 모든 면의 확률이 1/6으로 동일한 것을 예로들 수 있다.

 

- Berniulli Trial

: '베르누이 시행(Berniulli Trial)'이란, 결과가 두가지중 하나로만 반드시 나오게 되어있는 실험이나 시행을 의미한다.

대표적인 예시로 동전 던지기에서 Sample Space가 {앞면, 뒷면}인 것을 들 수 있다.

 

- Binomial Distribution

: 한국어로 '이항 분포'로, n번에 시행에서 해당 Sample Space가 x번 나올 확률은, 아래의 공식과 같으며,

p는 각 시행마다 해당 Sample Space가 나올 확률을 의미한다.

고등학교때 많이 보던 공식

 

그리고 n이 무한히 커질 수록 Central Limit Theorem, 중심 극한정리에 의해 가우시안 분포곡선과 비슷해진다

 

○ Continous Random Variable 

- Continous Uniform Distribution

: Discrete Uniform Distribution과 마찬가지로, Sample Space내에 모든 확률이 동일한 경우를 의미한다.

단, Continous Random Variable은 Sample Space가 Continous하므로, 딱 한지점의 확률은 0에 수렴하지만

모든 지점 확률의 합은 1이 된다.

대표적인 예시로, 원반을 던졌을때, 떨어진 원반의 모양이 딱 정확하게 특정한 각도로 존재할 확률은 0에 수렴하지만

0도부터 360도 사이 모든 각도의 확률을 더하면 1이되는 것과 같다.

 

- Gaussian Distribution

Normal Distribution(정규분포)라고도 하며, 수집된 자료의 분포를 근사화하는데 자주 사용된다.

Random Variable X에대한 확률분포공식은 아래와 같다.

 

 

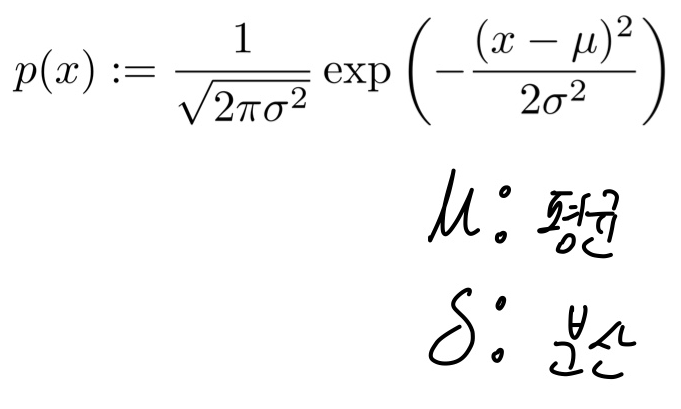
- Multivariate Gaussian Distribution

여러개 변수가 있을때 Gausian Distribution을 Graphical하게 표현하면 아래의 예시와 같이 표현할 수 있다. 

수식도 같이 적어놓았으니 한번 이해해보길 바란다.

2개변수의 Gaussian Distribution

○Expectation

기댓값(Expectation)은 각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값이다. 이것은 어떤 확률적 사건에 대한 평균의 의미로 생각할 수 있다.

기대값역시 Discrete Random Variable과 Continous Random Variable이 서로 다른데, 식으로 정리하면 아래와 같다.

- Discrete Case

- Continous Case​

​